Reflecting the directrix over the parabola
The following parametric equations are the result of reflecting the directrix of the parabola y = x 2 over the parabola y = x 2 :
x = 2 t − a t 3
y = b t 2 + 4 1
Submit your answer as b − a .
(The first one to post a solution gets to choose which curve I reflect over a parabola next. No guarantees that I will be able to do it, but I will try.)
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Do I get to choose the next curve?
Log in to reply
I will do my best.
Log in to reply
I've just been playing with reflections of more general lines - some pretty crazy curves come out! The link below should take you to a GeoGebra page that'll let you explore these:
Log in to reply
@Chris Lewis – That's very cool! Thanks for sharing!
Log in to reply
@James Wilson – Now I'm doubting myself. How would you reflect a point from "inside" the parabola? (ie a point ( x , y ) where y > x 2 .) Since it lies on multiple normals, it should have multiple reflections, but I'm not sure my method captures that.
Log in to reply
@Chris Lewis – Now that you mention it, something doesn't look right with the plots. In some cases, you have the curve and the line on the same side of the parabola.
@Chris Lewis – Nevermind. I see where that part of the curve comes from now.
Log in to reply
@James Wilson – You beat me to it - I was going to ask for the reflection of a unit circle in the parabola, but you've just posted about reflecting a parabola in a circle! Weird coincidence. Here's the circle reflected in the parabola:
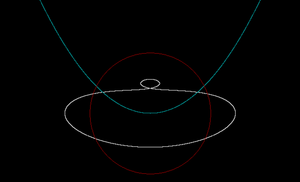
Log in to reply
@Chris Lewis – That's pretty funny. Alright, I'll get my engine started and get to it!
@Chris Lewis – So, I get a cubic equation in t , the parameter of the parabola. I could sample points on the circle and then use an equation solver to approximate the value of t and then plot all those points, but I'm afraid I'm not computer savvy enough to do that. Maybe it would be a good opportunity for you to teach me how to do it. If you don't mind, that is...
Log in to reply
@James Wilson – I'm still trying to think of a "proper" way to do this, but the way I plotted the previous image was more or less as you described: I sampled points on the circle, then worked out where they would reflect to through the parabola. As you say, you get a cubic doing this. Points "inside" the parabola lie on multiple normals, so have multiple images under reflection: this corresponds to when the cubic has more than one real root.
If the point on the circle is P ( cos θ , sin θ ) , we first need to find u such that P lies on the normal to the parabola through ( u , u 2 ) . The gradient of this normal is − 2 u 1 ; so we need to solve u − cos θ u 2 − sin θ = − 2 u 1
ie find the roots of f ( u ) = u 3 + 2 u − u sin θ − 2 1 cos θ = 0
Newton-Raphson works well to find one of these roots, say u 1 . Say the other roots are u 2 , u 3 . Then by Vieta, u 2 + u 3 = − u 1 and u 2 u 3 = 2 u 1 cos θ
This gives a quadratic in u 2 , u 3 . Checking the discriminant shows whether the remaining roots are real.
So now we've got (approximations to) all the real roots; we just need to do the reflections, but this is easy; the image points are ( P i ′ ( 2 u i − cos θ , 2 u i 2 − sin θ )
Of course, this is definitely quick and dirty: it's not an elegant way of finding the roots, but it works well enough to see the shape of the curve, which is what I wanted. I did this in QBasic (!) but there are better languages to use that will already have root-finding libraries (eg Python, Mathematica, MatLab) and be far more accurate.
Log in to reply
@Chris Lewis – That's quite an ingenious way of finding the other two roots. I appreciate you sharing that with me. You are helping to strengthen my abilities. I wish I could afford afford Matlab or Wolfram Alpha Pro. That or learn Python. I didn't know Python had stuff like that built-in.
Log in to reply
@James Wilson – By the way, thanks for making me go through the code again - I realised I had an error in my cubic so I've now corrected the earlier image.
Log in to reply
@Chris Lewis – Ah, ok. No problemo.
@Chris Lewis – Hi again. How are you doing Chris Lewis? I'm trying to graph more than two 3D space curves on a plot at once, but I can't find a program online that will let me do that. You wouldn't happen to have any suggestions, would you?
@Chris Lewis – Hello, Chris Lewis. I just wanted to let you know I enjoyed the mental stimulation you provided, even though I could not do the problem you gave me. Maybe one of these days, if I ever get the right program, I will come back to do some plots. I would like to add an animation to one of my problems ([Colliding Spring System]{https://brilliant.org/problems/colliding-spring-system/?ref_id=1609511}), but I am embarrassed that I have no earthly idea how to do that. You seem computer savvy. If you're willing to help me learn how, that would creak the door open a little further for me. If not, I wouldn't think any less of you.
Log in to reply
@James Wilson – Thanks, and likewise - it's definitely fun to explore this idea of reflections through a curve.
Now, I just revealed I was using QBasic there ;-), but depending on the type of animation you're after, gifsmos is great for animating graphs. Essentially it's desmos but you can save gifs from it.
Otherwise there are various free gif makers around that let you upload a deck of frames.
I'm probably not the best placed to advise on animations but some users on here are very good at them - it might be worth either replying to one of those or setting up a discussion on the topic (I'd like to get better at this too!). I seem to remember some very nice animated solutions to the daily problems - that might be a good starting point.
Log in to reply
@Chris Lewis – I bet Maple could solve the (spring) matrix equations and do an animation. I don't have Maple though. I asked Chew-Seong Cheong for some advice. Maybe he can help make this animation a reality.
Log in to reply
@James Wilson – Mahdi Raza is great at these. See here for example.
Log in to reply
@Chris Lewis – Really? How can I attempt to contact him?
Log in to reply
@James Wilson – If you go to that problem, his (animated) solution is the first one. You can click to his profile from there and respond to a more recent problem or solution; or if you start a discussion you can flag him by typing an "at" symbol before his name (make sure you get the right one, though, there are a couple of people with the same name on here).
Log in to reply
@Chris Lewis – Thanks for the help. I really appreciate it. I am working on a problem now that will knock your socks off. Hopefully, I am successful. I can almost taste the solution.
That looks like a very intelligent solution. It is simpler than mine. Your graph matches mine. How did you know the reflected point would have coordinates ( 2 u − v , 2 u 2 + 4 1 ) ?
Log in to reply
Thanks! The point A is the midpoint of the points P and P ′ ; so (if we abuse notation and just treat these as position vectors) P + P ′ = 2 A and P ′ = 2 A − P .
Log in to reply
Ah, I see. I used a general formula for the reflection of a point over a line.
The numerator in my expression factors and one of the factors cancels with the denominator. I didn't realize it. Let me see if I can change it to its simpler form.
Log in to reply
Gah, yes, that makes sense. That would have made the end of my solution simpler!
To find the reflection of a point P through a curve C , we find the normal to C that contains P ; P is then reflected through the corresponding tangent to C :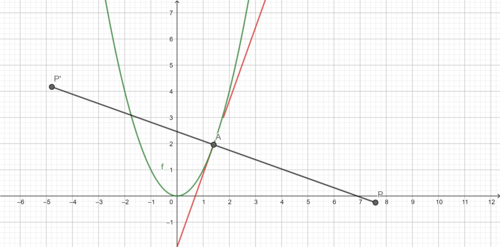
(image produced with GeoGebra.)
To reflect a line, we can just do the same thing for each point on the line.
Say C is the parabola y = x 2 . The directrix of C is y = − 4 1 . Consider a point P ( v , − 4 1 ) on this line, and say it's reflected through the tangent to the point A ( u , u 2 ) on the parabola.
P lies on the normal to C through A ; so basic coordinate geometry tells us u − v u 2 + 4 1 = − 2 u 1
which solves to v = 2 u 3 + 2 3 u
The reflected point will have coordinates P ′ ( 2 u − v , 2 u 2 + 4 1 ) ; ie P ′ ( 2 u − 2 u 3 , 2 u 2 + 4 1 )
Since each u has a corresponding v , this gives a parametric equation for the reflection curve: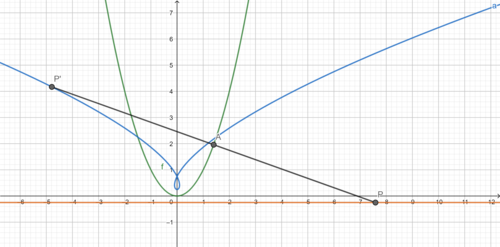
Obviously, the form of this parametric equation is different from the one in the question. But we can just plug in a couple of values of t to get a system of simultaneous equations; we find a = b = 2 and a − b = 0 .