Driver, Chase That Angle!

Geometry Level 2

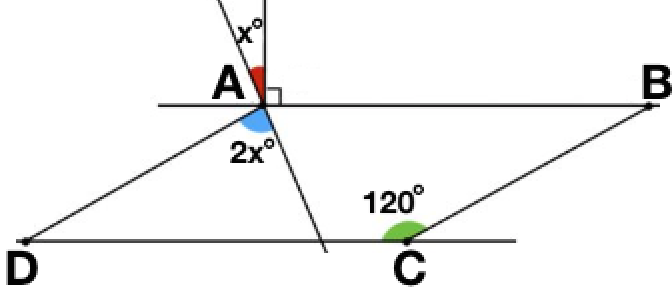
In the figure above, line segments $AB$ and $CD$ are parallel. Find $x.$

45 30 15 40

8 solutions

Dan Li
Aug 9, 2016

this problem is unsolvable with the information provided.

I agree because it doesn't say that also ACted and BDSM are parallel

Evi Sahini - 4 years, 4 months ago

Correct. How can they post a problem so obviously missing relevant information ?

tom paine - 4 years, 4 months ago

It's definitely solvable, you just aren't brilliant. I looked at the angles of x° and 90° and realized they are on one line. Knowing that it is one straight line, you know that all the angles added up equal 180°. So with that information you can find that the other angle would be 90-x. Then you set 2x°+(90-x) equal to 120° and you end up with x=30°.

James Thompson - 4 years, 4 months ago

"Then you set 2x°+(90-x) equal to 120° and you end up with x=30°" this can only be done if ABDC is a parallelogram, since opposite angles in a parallelogram are congruent. otherwise we dont know the measure of angle CAB

Christian Glover - 4 years, 4 months ago

We don't know that AD is parallel to BC. We need more information.

Martine Suid Jaffe - 4 years, 3 months ago

Zandra Vinegar Staff
Sep 28, 2015

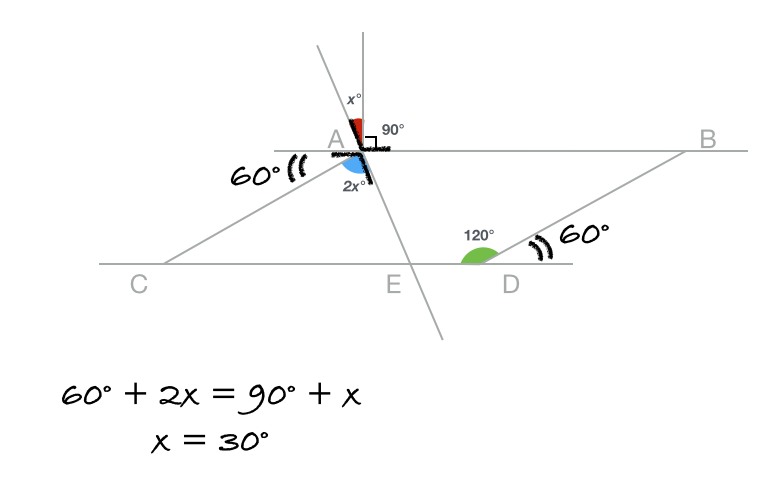
The two 60° angles drawn in below are equal because they are opposite interior angles. We know that the lower right one measures 60° because the given 120° angle and it make a 180° line together. Then, we can use the fact that $x + 90$ and $2x + 60$ are vertical angles and therefore equivalent to solve for $x$ .

You should specify in the problem that lines AC and BD are parallel.

Mark C - 5 years, 3 months ago

Apologies, that got mistakenly cut from the problem's statement. I've corrected the lapse! :)

Zandra Vinegar Staff - 5 years, 2 months ago

Unfortunately I must disagree, you haven't corrected the lapse. We are given that horizontal line segments AB and CD are parallel, which is necessary to solve the problem. However, using your solution's notation, we need the information that AC and BD are parallel as well (NB the solution's notation of C and D switch the problem's notation of C and D).

Adam Davis - 4 years, 11 months ago

Seven months and problem statement still not corrected. This is a disappointment from Brilliance.org. I think your edit got lost. You should fix the problem and delete all the comments relating to the missing information once it is saved so people are not confused.

Bradley Slavik - 4 years, 3 months ago

From the information that was given you can not conclude that two angles that you designate as opposite and interior are equal! The problem states only that the horizontal lines are parallel! If you can prove that that lines AC and BC are parallel please show me! Otherwise I think you have a solution however erroneous!

Howard Griffin - 5 years, 2 months ago

This still needs corrected. Lines AC and BD must be stated as parallel. I had to assume it was the case.

Sean Bourelle - 4 years, 3 months ago

The wording still needs correcting

Ben Litterick - 4 years, 3 months ago

Love it. Your diagram is simple and needs no explanation.

Kerry Lasiter Billingsley - 5 years, 8 months ago

Kevin Elmore
Aug 7, 2016

The answer is easy enough, but I had to make some assumptions that were not listed in the original problem.

The original problem only said that AB and CD are parallel. To know for certain that the x=30, you have to know that AD and BC are also parallel. Perhaps just say that ABCD is a parallelogram.

Alternatively, knowing that the line intersecting AB is a straight line allows the puzzle to be solved. When dealing with many lines intersecting, it can be tricky to assume that two segments are part of the same line. In this case, it turns out to be true.

Anh Đức Trần
Sep 30, 2015

prolong the line that makes a right angle with AB, the angle 2x would be split into two equal ones, both of which are x. The ACD angle is 60 degree, and because the prolonged line make another right angle with CD (CD para AB ), x would be 90-60 = 30 degree.

How can the prolonged line split the 2x into two equal angles? please guide.

HIMANSHU PRAJAPATI - 5 years, 8 months ago

Because the prolonged line, one of the splitted angles'll be $x^0$ and the total angle is $2x^0$ . So it is splitted equally

Manish Mayank - 5 years, 8 months ago

It would split it in half, but only if you knew the answer beforehand. The problem here is the diagram is not drawn to scale, meaning it appears that the angle would not be in half. Either way the above solution is invalid due to the assumed fact that the angle is split equally.

Stewart Feasby - 5 years, 8 months ago

When we prolong the line perpendicular to AB, it cuts through AE... Now suppose that line cuts CE at F, then angle FAE would b equal to x as it is vertically opposite angle... If one part is x, then obviously second is also... Thus it practically divides it in two equal parts ;)

Saptneel Sharma - 5 years, 8 months ago

@Saptneel Sharma – You don't know that the line that forms the left hand side of angle x and "appears" to run diagonally down to the right is really one line. In other words you don't really know that the line that forms the left hand side of angle x is really a continuation of line EA. Unless that is indicated in the problem you dont know that. It appears to be continuous but appearances are deceiving.

Scott Shannon - 5 years, 8 months ago

@Scott Shannon – If that is to happen then th equation - 60' + 2x = 90' + x would also be wrong as that too won't form vertical angles. I guess it won't be possible to solve if that has to happen

Saptneel Sharma - 5 years, 8 months ago

Shuvo Das
Oct 1, 2015

2x+60+90-x=180; x=30

Sadasiva Panicker
Sep 30, 2015

Opposite angles of //grm are equal. So angle A =120, If the perpendicular extends downwards, so formed vertical opposite angles x, . Therefore x+x+90 = 120, Then 2x = 60. So x = 60/2 = 30. ,

How did you conclude that the figure was a parallelogram?

Stephen Clarke - 5 years, 3 months ago

That fact was given in the original problem statement and then accidentally cut out in a recent edit. And I just added it back in! :)

Zandra Vinegar Staff - 5 years, 2 months ago

Nope. Still not there. Your edit got lost.

Bradley Slavik - 4 years, 3 months ago

Omar Monteagudo
Jan 18, 2017

You do NOT know that the transverse lines are parallel.

tom paine - 4 years, 4 months ago

Hi, Tom:

Actually the problem states that they are parallel indeed (AB and CD). As for the other two, you are right, It is just an assumption that I did. I haven't thought in the case the are not. I'll do it later and I'll comeback to share what I would have found.

Omar Monteagudo - 4 years, 4 months ago

J Chaturvedi
Mar 17, 2016

The angle diagonally opposite to 120° is also 120°, so 2x+(90-x)=120. This gives x=30.

Driver, Chase That Angle!

8 solutions

0 pending reports