Related to Open Problem #1: Bishops and Knights

First, here is a possible 4 by 4 solution:

Now, let's eliminate the 3 by 3 case:

A knight can't be in the center because it will attack no squares.

A knight can't be in the corner because if bishops are placed at the only two attacked squares, the bishops attack each other, which is against the rules of the problem.

A knight can't be on the edge because if bishops are placed at the only two attacked squares, the bishops can attack one other knight only, which is against the rules of the problem.

Therefore 3 by 3 is an impossible scenario.

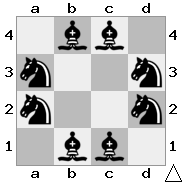
$\boxed{4 \times 4}$ is the smallest.

---

$(2 \times 2), (3 \times 3)$ are too small chessboards to satisfy the condition. $2 \times 2$ is obviously not a solution.

$3 \times 3$ will not work for some reasons. Considering different configurations.

• It has only 9 squares. So it will be difficult to satisfy the condition.

• While a knight can attack exactly two bishops, bishops can't attack the knight or any other knight.

• While a bishop can attack exactly two knights, knights can't attack the bishops.

• Bishop can attack each other, knights can attack each other.

Hence $3 \times 3$ will not work.

1. Knights always attack pieces on their opposite color.
2. Bishops always attack pieces on their same color.
3. Thus a pair of knights will attack a pair of bishops who cannot attack them back .
4. To satisfy the rules, these bishops must then attack a different pair of knights on their same color, which knights in turn must attack another pair of bishops on their opposite color, who then attack the original knights.
5. This creates a symmetrical attack chain that requires (a) exactly two of each piece on each color, and (b) a same-color pair of knights must jointly attack the same two bishops on the opposite color, and (c ) each same-color pair of bishops must jointly attack both of the knights on their color.

There are only 2 ways to place 2 knights so they attack the same 2 squares (bishops), if we count 90-degree rotations as equivalent. (These 2 knight configurations are illustrated in the 4x4 and 5x5 solutions shown by other posters, so I won’t redraw them here.) One of these knight configurations spans 4x4 squares (including the two attacked squares); the other configuration spans 3x5 and squares. Thus a 4x4 grid is the minimum even conceivable in our analysis so far (and 1x1, 2x2, and 3x3 squares are thus disqualified).

The only way to place 2 bishops so they attack the same 2 squares (knights) is by placing them at opposite vertices of a rectangle (rotated 45 degrees so its sides run through same-color diagonals on the board). Within a 4x4 grid, there are 2 ways to do this (plus their 90-degree rotational transformations): (A) at the top center and bottom center cells of a 3x3 grid, and (B) at opposite corners of a 2x4 grid.

Under option A, the attacked squares do not match the required knight configuration described above, so it is disqualified. Option B matches the required knight placement.

These are quite tight constraints, leaving only 1 possible knight configuration and 1 matching bishop configuration. Start with either of these (knight or bishop) configurations; place opponent pieces in their jointly-attacked squares; repeat two more times, and you have the (only) 4x4 solution (plus its rotations/reflections, of course).

There are 630 ways to arrange the 4 knights and 4 bishops on a 3X3 board: There are 9 (9 choose 1) possible empty spaces and for each choice of empty space there are 8 choose 4 ways to arrange the remaining pieces. The bishop constraint requiring it to be able to attack at least 2 spaces means the bishop cannot be on any corner space. Thus the remaining 5 non-corner places must hold 4 bishops and clearly there are 5 (5 choose 4) scenarios, each not meeting the constraint the bishops cannot attack one another. Thus, 3X3 is impossible.

There are 900,900 ways to arrange the 4 knights and 4 bishops on a 4X4 board: (16 choose 8)*(8 choose 4). Again, the bishop constraint drastically reduces this number: No corner spots leaves 12 places for 4 bishops for 495 possible ways. Due to the symmetries of the board, a solution is quickly found by first trying a bishop on the non-corner edge (all non-corner edges are equivalent because of symmetries). The 4 center squares are also equivalent, but there are 4 compared to 8 and we know at least one has to be a non-corner edge due to the bishops can't attack bishops constraint (can't all be in center). From here placing 2 knights so that the non-corner edge bishop is attacking them, the solution (with the same symmetries manifested) is evident with minimal trial and error: All pieces on non-corner edges, paired with a same piece partner and opposite the equivalent pair.

Hi there, I've been lately learning Prolog and I wanted to test what i learnd with this problem, I made a program that gives you all possible solutions for a chessboard of N size, I'm still a beginner so I'm pretty sure this program can be a lot more optimized, it can be modified to play with more chess pieces and also other types.

There may be some typos after copy/pasting and formatting. (if there is something in italic, it meant to be a _).

%START

%I used Swi-Prolog for this program.

%4k4b

%Ahmed Amrani Akdi

%

% Gives combinations of elements from a list.

comb(_,[]).

comb([X|T],[X|Comb]):-comb(T,Comb).

comb([_|T],[X|Comb]):-comb(T,[X|Comb]).

% i used combinations of 4 elements from 16, otherwise, the program would pick variations and thats 4! more times.

%

% Creates a list of the positions of the N-size chessboard.

create([N1,N2],[N3,N4],[XY|Tail]):-

N2=<N4,N1=<N3,

XY=[N1,N2],

M is N2+1,

create([N1,M],[N3,N4],Tail).

create([N1,N2],[N3,N4],List):-

N2>N4,N1=<N3,

K is 1, M is N1+1,

create([M,K],[N3,N4],List).

create([N1,_],[N3,_],List):-

N1>N3,

List=[].

%

%Generates the possibles lists of positions for the knights and the bishops.

generatekb([N1,N2],[N3,N4],[X,Y,Z,K],[X1,Y1,Z1,K1]):-

create([N1,N2],[N3,N4],List),

comb(List,[X,Y,Z,K]),

subtract(List,[X,Y,Z,K],Remainder),

comb(Remainder,[X1,Y1,Z1,K1]).

%

% i had to separate the attacks to make it easier for the program to detect errors and backtrack

%bishop vs knight

bishop_attack_knight([],_):-!.

bishop_attack_knight([A|List],List1):-

oneb_attack_knight(A,List1,0),

bishop_attack_knight(List,List1).

%

oneb_attack_knight(_,[],R):-!, R=2.

oneb_attack_knight([X0,Y0],[[X,Y]|List1],Cont):-

((Y is (X+Y0-X0); Y is (-X+X0+Y0)),!,

M is Cont+1,

oneb_attack_knight([X0,Y0],List1,M));

oneb_attack_knight([X0,Y0],List1,Cont).

%

%bishop vs bishop

bishop_attack_bishop([],_):-!.

bishop_attack_bishop([A|List],List1):-

oneb_attack_bishop(A,List1,0),

bishop_attack_bishop(List,List1).

%

oneb_attack_bishop(_,[],R):-!, R=1.

oneb_attack_bishop([X0,Y0],[[X,Y]|List1],Cont):-

((Y is (X+Y0-X0); Y is (-X+X0+Y0)),!,

M is Cont+1,

oneb_attack_bishop([X0,Y0],List1,M));

oneb_attack_bishop([X0,Y0],List1,Cont).

%

%knight vs knight

knight_attack_knight([],_):-!.

knight_attack_knight([A|List],List1):-

onek_attack_knight(A,List1),

knight_attack_knight(List,List1).

%

onek_attack_knight(_,[]):-!.

onek_attack_knight([X0,Y0],[[X,Y]|List1]):-

not((Y is Y0+1, X is X0+2);

(Y is Y0+2, X is X0+1);

(Y is Y0+2, X is X0-1);

(Y is Y0+1, X is X0-2);

(Y is Y0-1, X is X0+2);

(Y is Y0-2, X is X0+1);

(Y is Y0-2, X is X0-1);

(Y is Y0-1, X is X0-2)),!,

onek_attack_knight([X0,Y0],List1).

%

%knight vs bishop

knight_attack_bishop([],_):-!.

knight_attack_bishop([A|List],List1):-

onek_attack_bishop(A,List1,0),

knight_attack_bishop(List,List1).

%

onek_attack_bishop(_,[],R):-!, R=2.

onek_attack_bishop([X0,Y0],[[X,Y]|List1],Cont):-

(((Y is Y0+1, X is X0+2);

(Y is Y0+2, X is X0+1);

(Y is Y0+2, X is X0-1);

(Y is Y0+1, X is X0-2);

(Y is Y0-1, X is X0+2);

(Y is Y0-2, X is X0+1);

(Y is Y0-2, X is X0-1);

(Y is Y0-1, X is X0-2)),!,

M is Cont+1,

onek_attack_bishop([X0,Y0],List1,M));

onek_attack_bishop([X0,Y0],List1,Cont).

%

%attacks

war(Listk,Listb):-

bishop_attack_knight(Listb,Listk),

bishop_attack_bishop(Listb,Listb),

knight_attack_bishop(Listk,Listb),

knight_attack_knight(Listk,Listk).

%

% [N1,N2] is the size of the chessboard, Listk the list of knights and Listb the list of bishops.

solution([N1,N2],Listk,Listb):-

generatekb([1,1],[N1,N2],Listk,Listb),

war(Listk,Listb).

%END

Different chess prieces can be used, their attack conditions must be defined, say, "knight attack knight and onek attack knight".

More chess pieces can be used also, a modification of the lists is needed.

Also keep in mind, that the higher N is the more time the computer needs to find solutions.

Basically this is the skeleton.

Here is an image:

I'm open to criticism.

First, the question is about the objects' next moves. In order for the knight to engage the bishop, it needs to be in a 2 by 3 range. That makes the complete L motion. A bishop can be positioned anywhere diagonally (on the same color and path), from the knight.

Then, the question asks for the smallest battleground. 2 by 3 is the minimum for an attack, but for two pairs you need (2×3)+(2×3) amount of space.

12 is 4 by 3 or whatever factors you'd like, but this battle formation needs structure. The four opposing, attacking and defending pairs of pieces would need their own domains so as to not block their partners' moves. 4 by 4 was the most appropriate and minimal answer.