Related to Open Problem #1: Knights and Kings unlimited!
On an infinitely large chess board, is there a configuration of kings and knights such that each king attacks exactly 2 kings and 2 knights, and each knight attacks exactly 2 kings and 2 knights?
This problem is part of the new Brilliant.org Open Problems Group (see Open Problem #1 ).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
A white knight DOES not attack another white night, and a king CANNOT attack another king of any color.
Log in to reply
You need not think lie a chessman; Think in terms of MATHS THE LANG. IS NOT MADE CLEAR ALTHOUGH
see we don't need any pattern for the answer you r not asked to map the pieces to each other; you can think interns of distinct blocks SINCE THE BOARD IS INFINITE WE HAVE ENOUGH ROOM TO PLACE ANY OF THE PIECES WE WANT; KEEPING SUFFICIENT GAP IN BETWEEN IN ORDER TO AVOID MULTIPLE ATTACKS;;;
TRY THIS https://brilliant.org/problems/pental-bogda/?ref_id=1433431
https://brilliant.org/problems/pental-bogda/?ref_id=1433431
There exists a pattern which can be used to fill the infinite grid as follows:
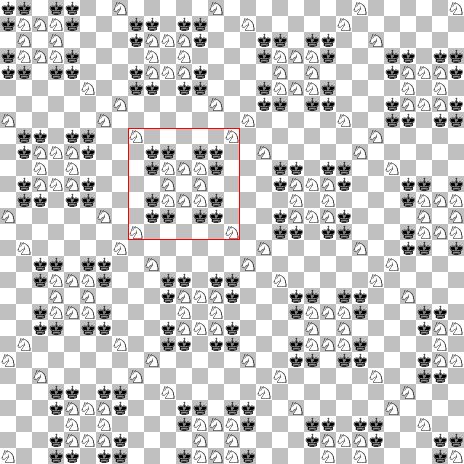
Can you find more of them?
Hey, I can but I can't because I wanna make an image. How did you made it? Thanks!
Log in to reply
You can do it with a chess problem diagrams package for LaTeX, but honestly, I was too lazy to use it so I just copied a picture from the internet, and edited it using Paint. xD
Log in to reply
Thats amazing! I didn't knew bout that package! Thanks.
Log in to reply
@A Former Brilliant Member – No problem :)
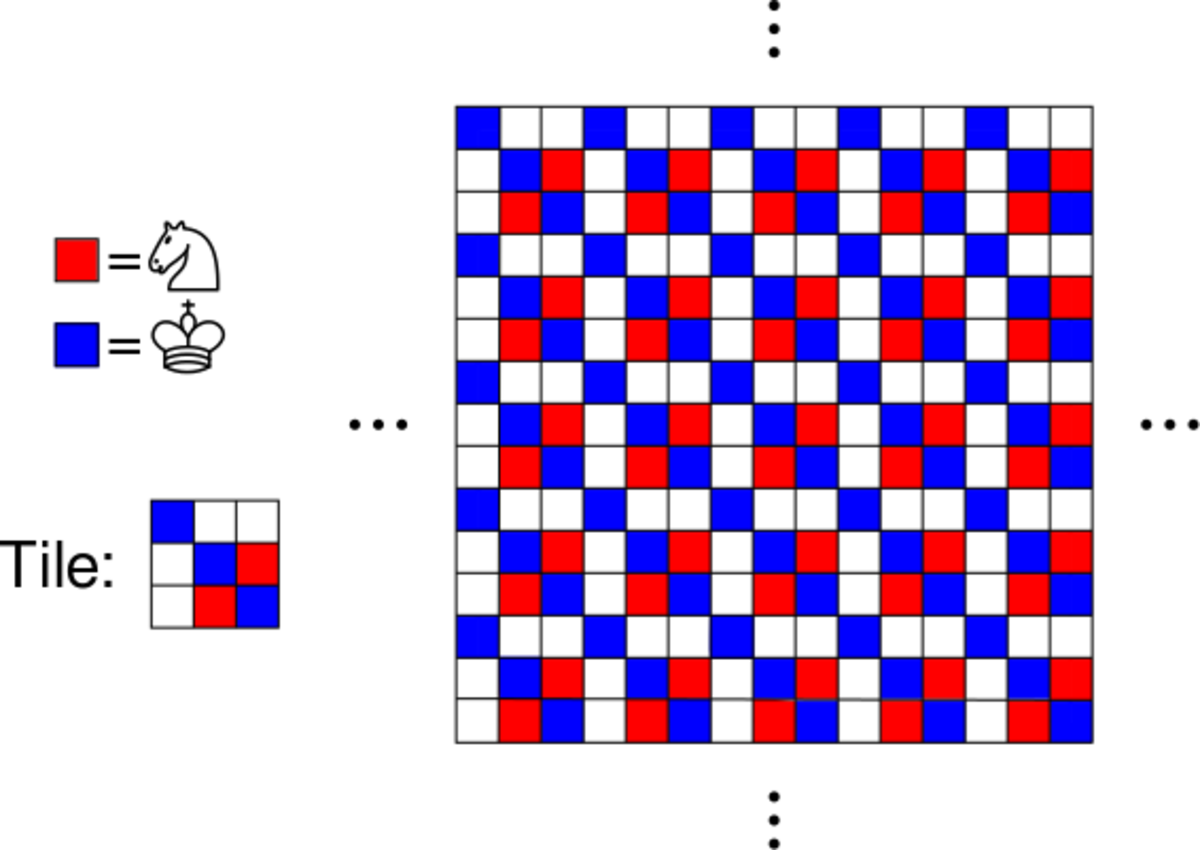
Yep, here's another one: Infinite Grid Assume that the red squares are occupied by knights and the blue squares are occupied by kings.
A white knight DOES not attack another white night, and a king CANNOT attack another king of any color.
see we don't need any pattern for the answer you r not asked to map the pieces to each other; you can think interns of distinct blocks SINCE THE BOARD IS INFINITE WE HAVE ENOUGH ROOM TO PLACE ANY OF THE PIECES WE WANT; KEEPING SUFFICIENT GAP IN BETWEEN IN ORDER TO AVOID MULTIPLE ATTACKS;;;
CHECK THIS: https://brilliant.org/problems/pental-bogda/?ref_id=1433431
Here's another infinitely tiled pattern, with uneven numbers of kings and knights (3 kings for every 2 knights):
 Additionally, if the pattern is mapped onto a torus, it would work on its own:
Additionally, if the pattern is mapped onto a torus, it would work on its own:
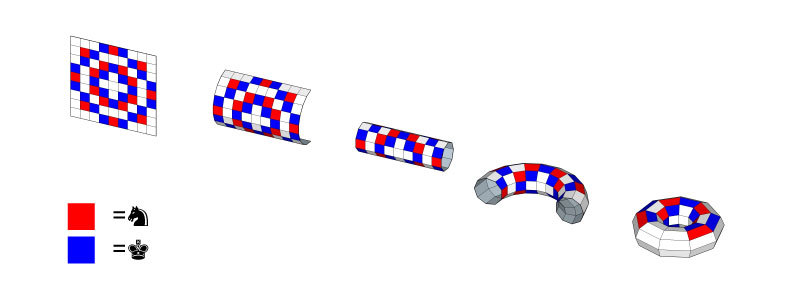
While working out the corner problem
here
, I also found this infinitely tiled pattern (interestingly, also 3 kings for every 2 knights):

see we don't need any pattern for the answer you r not asked to map the pieces to each other; you can think interns of distinct blocks SINCE THE BOARD IS INFINITE WE HAVE ENOUGH ROOM TO PLACE ANY OF THE PIECES WE WANT; KEEPING SUFFICIENT GAP IN BETWEEN IN ORDER TO AVOID MULTIPLE ATTACKS;;;
https://brilliant.org/problems/pental-bogda/?ref_id=1433431
. CHECK MY PROBLEM
I'm not picture savvy but this is easy to describe:
Of three rows:
Make the middle an infinite row of Kings with knights in every third position in the row above and every third position in the row below, offset by 1.
(The Kings are fulfilled, but the knights only attack one knight at this point.)
Next row all blanks.
Next three rows same as first three, again offset by 1.
(Makes the knights attack one knight across the blank row.
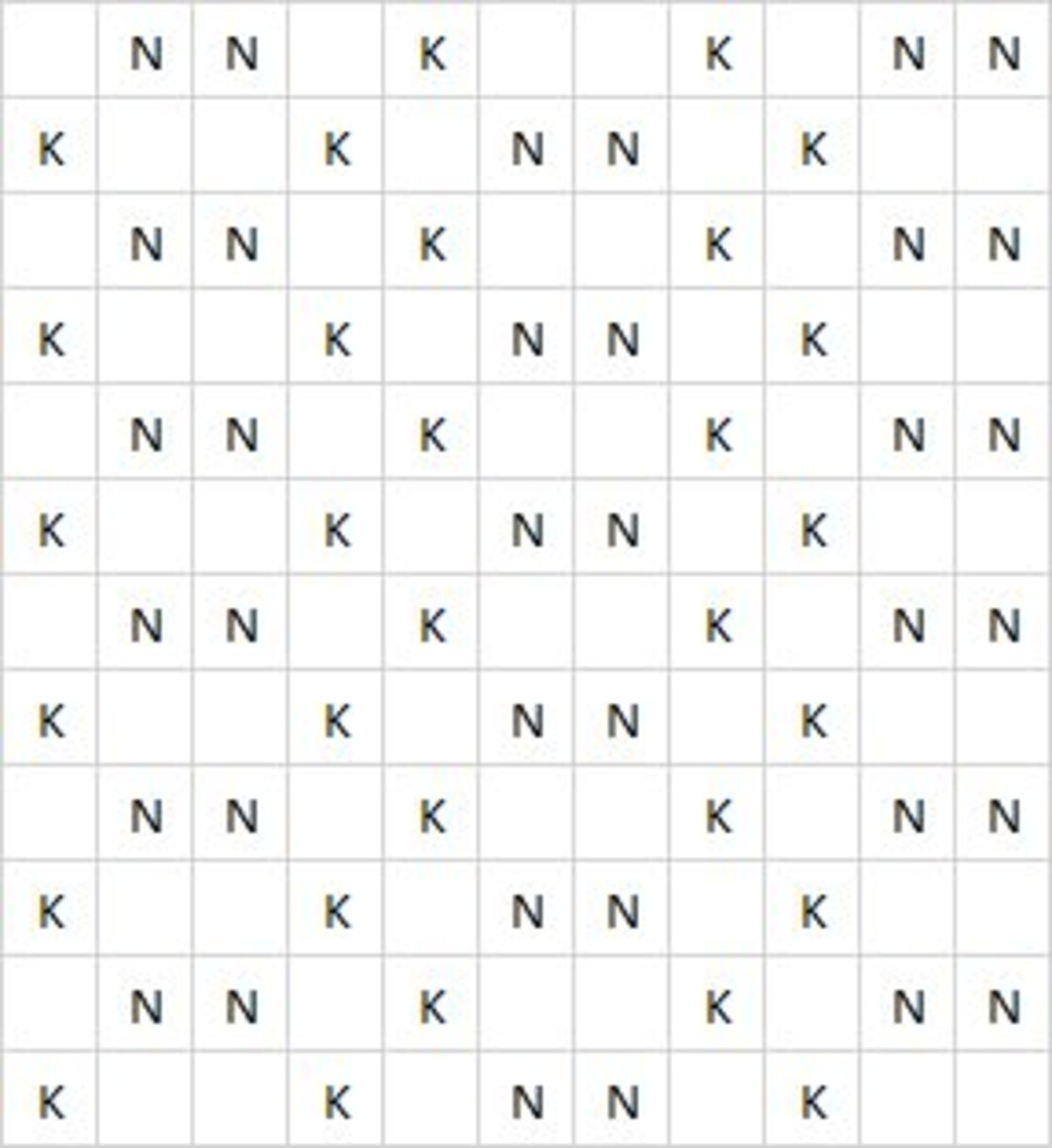
Assume the pattern continues indefinitely.