Relative Stuntmen Motion
A villain (in red) jumps from a building, and then 2 s later a superhero (in blue) jumps after him from the same height.
As they're both falling, how does the distance change between them?
Assume that the villain and hero have identical shape and mass.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Once the villain begins to approach terminal velocity, it might be possible to catch up, if the superhero changes into a more aerodynamic position. In that case the superhero's terminal velocity can be greater, so the distance will decrease again, and it doesn't necessarily have to end when the villain hits the ground first.
Also, assuming the superhero has superpowers, I'm also sure that he probably has some means of accelerating in air apart from gravity. Otherwise jumping to his own death would be a bad idea...
Not sure how to comment directly to the question instead of to a solution which is what it seems like I am doing...
The problem is somewhat misleading, because it says that both parties "jump" from the building, rather than "fall". That means each exerted a force, and as such, the velocities of both depend not only on gravity but also on the force they exerted. So the superhero could potentially catch up by exerting a sufficiently greater initial push during their jump.
Log in to reply
Hit "More" in the bottom-right of the problem and submit a report.
It is clear that the villain and hero jump perpendicular to the building. Therefore, the velocities of each jump would not be directed toward the ground.
Kind of a misleading question yes the first jumper will move away from the second but they will both reach terminal velocity at which point the relative distance will stabilise
another factor not mentioned is the air resistance on the first jumper would be more than the second who is right behind (drafting)? less wind friction?
Log in to reply
See @Justin Llanos's report and the comment on it.
This was my thought as well. This should be noted in the question.
Agree with that. The question should explicitly state that they are falling in vacuum with oxygen masks on.
exactly, which would slow him more than the upper jumper
My opinion is that the second jumper should reduce the distance a bit because of lesser wind friction slowing the first jumpers decent more than the second jumpers. Just like formula one drivers when they are racing. They have the same engine sometimes, but use the less resistance to catapult themselves past a previous car.
The distance is surely going to decrease once the first jumper hits the ground and is not moving...
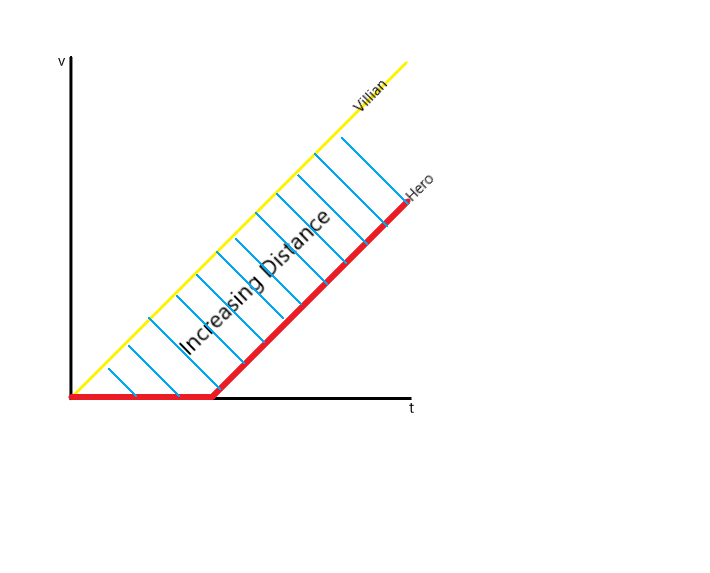
Because the villain jumped first, when the hero jumps down, his speed is always slower than the villain. Since the speed of the villain is always faster than the hero, the distance will increase.
There should be a final speed limit for both. As the blue jumper reaches that speed limit they will both fal at a constant speed and hence maintain the same distance between them.
Log in to reply
Love that graph.
Log in to reply
Thank you!
Personally, i consider that graph a red herring. Seeing the speeds does VERY little to help visualize the distances... :-|
This, of course is true in space. On earth within 10sec they will reach terminal velocity and the distance will remain constant. When air is taken into consideration, the angle of the body relative to the wind is also a factor that needs to be taken into consideration. Falling heads down is much faster than falling belly down
Jeez been watching too many movies
In real case they would reach final speed du to a air drag.
Both jumpers will approach the terminal velocity. This occurs when the air resistance (which increases with speed) eventually balances the gravitational force on their bodies (which remains constant). So in the long run both jumpers will be falling at the same speed and the distance between them will remain constant.
I guessed that this was not the answer that Pranshu was looking for, and so made the assumption that we should ignore the effects of air resistance. In that case we can observe the situation from a free float frame which is falling with the second jumper towards the earth. In this frame of reference there appears to be no forces acting on either jumper, so by Newton's first law, each one continues 'in a state of rest or of uniform motion in a straight line.' So the second jumper remains at rest and the first one just continues drawing away from him with the velocity he has reached at the time the second one leaves the building. ( g Δ t in the obvious notation).
How about all of them! Initially the separation will increase. The rate of increase in separation will decrease as the jumpers approach terminal velocity at which point (assuming the building is tall enough) the separation will remain constant until the villain hits the ground at which point the separation will rapidly decrease until the hero hits the ground. From that point on the separation will remain zero. - assuming neither runs off or bounces after they hit.
From what I'm learning from my high school physics class, this is true. Pranshu should have specified whether or not we should factor in air resistance/terminal velocity.
It's reasonably likely that the jumpers would reach the ground before achieving terminal velocity. Searching around a bit, it seems that a typical terminal velocity would be between 50-60 meters/second. I.e., 5-6 seconds after jumping. So a building could be as tall as 150 meters without terminal velocity being an issue. Yes, there are plenty of taller buildings than that, but there are even more tall buildings that aren't as tall as that. Also one can achieve a much higher velocity by intentionally presenting a small cross section.
I agree. My calculation was the same as peter
The two characters are accelerating at the same rate. Let t = 0 describe the moment the superhero starts falling; let y 0 be the distance fallen by the villain before this moment and v 0 the villain's speed at that time. Then we may write y sh y vil = 2 1 g t 2 ; = 2 1 g t 2 + v 0 t + y 0 . The distance between them is Δ y = y vil − y sh = v 0 t + y 0 ; in other words, the villain moves relative to the superhero at a constant speed of v 0 . Thus the distance between them (which was initially y 0 ) will only increase.
Arjen --- In your delta(y) equation you have t(vil) - t(sh) in the 'middle'. Shouldn't that be y(vil) - y(sh) (i.e. y instead of t) ?
Log in to reply
You are right. I'll correct it.
Log in to reply
One of these days I must learn the LaTeX code. When you insert something using that code, do you have to type LaTeX: first ?
Let us first assume that the effect of air resistance is negligible.
By using x = u t + 2 1 a t 2 , the displacement of the villain, x V , can be written as
x V = 2 1 g t 2
where we take downward direction as positive.
The superhero jumps after the villain with a time delay of T , thus the displacement of the superhero, x H , is
x H = 2 1 g ( t − T ) 2
The distance between both of them is basically the difference in their displacements
Δ x = x V − x H = 2 1 g t 2 − 2 1 g ( t − T ) 2
which boils down to
Δ x = 2 1 g T ( T + 2 t )
It can be seen that the distance between both characters increases with time.
If air resistance were to be taken into account, then initially both the villain and superhero would experience negligible air resistance since their velocities are small (drag force is dependent on velocity) so the distance between them would follow the behaviour described above.
As their velocities increase, the villain would experience a larger drag force because the villain is falling with higher velocity, which means that the villain will decelerate at a faster rate than the superhero. Therefore the distance between them will decrease.
As the drag force acting on the villain become equal and opposite to the weight of the villain, the villain is falling at terminal velocity whilst the superhero continue to decelerate. Once both of them are falling with terminal velocity the distance between them will remain constant.
Until they reach terminal velocity their distance will increase. Because the first jumper will be traveling faster. Am I missing something or should this problem give a timeframe?
Yes. Should give a timeframe.
From the moment the second jumper jumps until both jumpers achieve a terminal velocity, the second jumper has less velocity than the first jumper. Thus the distance between the two jumpers will increase.
In the most basic terms, in that 2 seconds, the villain has already “overcome” acceleration and is going close to top speed. So when the hero jumps, he has to overcome acceleration while the villain is in his top speed. Thus, the distance between them increases.
Can’t the height of the two while they are falling be represented through a parabola?
Since the hero travels the same distance in the same amount of time as the villain (just 2 seconds behind), the time interval between them remains a constant 2 seconds. That is, checking the position of the villain at any given time, the hero will reach that position 2 seconds later. Since the hero's velocity is increasing, the distance covered in those 2 seconds is also increasing.
(Naturally this holds only until the villain hits either terminal velocity or the pavement, whichever comes first.)
Let's be more mathematical, the first superhero's height from the initial point be h 1 = 2 1 g t 2 , then assume after T seconds, the second superhero also dropping down, and his height from the initial point is h 2 = 2 1 g ( t − T ) 2 and domain is t ∈ [ T , ∞ ] . Since the value of h 1 always bigger than h 2 , then the distance would be d = h 1 − h 2 = 2 1 g [ t 2 − ( t − T ) 2 ] = 2 1 g [ 2 t T − T 2 ]
Now we see d is a linear function of t , having a positive slope, so d is Increasing .
Kelvin -- You stated that h is height from the initial point. Should h be given as, say, y or d instead of h (so as not to confuse it with height above the ground) ? Also, you stated that the value of h2 is always bigger than h1. Don't you mean instead that h1 > h2 ? This is because at T seconds the first jumper will be some distance d1 (h1 in your text) from the jump point - while the second jumper's distance d2 (h2 in your text) from the jump point is essentially zero. Just some thoughts from a math-challenged small-town hick. Please advise. :-)
Log in to reply
Oh yes, there is a typo, I have corrected it. Thanks!
Log in to reply
If there is air friction then after both men reach the terminal velocity the distance between them doesn't change anymore
A plain old hero would fall, of course, but this is specified as a SUPERhero, in which case WHICH superhero matters. Some superheroes have the ability to accelerate when flying (for example, Superman). In his backstory, the flying was explained away as just a very powerful jump because his muscles were used to the higher gravity of Krypton, but that got perverted over time to the point that he was able to fly in rings around the sun (which somehow managed to reverse time?). Obviously that requires the ability to accelerate in midair, physics be damned,
F r o m t o p , d i s t a n c e D v o f v i l l a i n , t s e c o n d s a f t e r j u m p o f h e r o , D v = 1 / 2 g ∗ ( t + 2 ) 2 . T h e n , d i s t a n c e D h o f h e r o f r o m t o p , t s e c o n d s a f t e r h i s j u m p , D h = 1 / 2 g t 2 . S o a t a n y t i m e t , f r o m s t a r t o f h e r o ′ s j u m p , s a p e r a t i n g d i s t a n c e D = D v − D h = 1 / 2 g ∗ ( t + 2 ) 2 − 1 / 2 g t 2 = g ∗ 2 + 2 ∗ g t . ∴ a s t i n c r e a s e s , D a l s o i n c r e a s e s l i n e a r l y . ∣ V i l l a i n h a s a d v a n t a g e o f c o n s t a n t s e p a r a t i n g d i s t a n c e o f 1 / 2 g ∗ 2 2 = 2 g . A L S O , v e l o c i t y o f 2 g . a t t h e s t a r t o f h e r o s j u m p T h i s v e l o c i t y i n c r e a s e s t h e s e p a r a t i n g d i s t a n c e b y 2 g ∗ t . D i n c r e a s e s w i t h i n c r e a s e o f t , t i l l v i l l a i n r e a c h e s t h e g r o u n d . F r e e f a l l i s a s s u m e u n d e r g r a v i t y o n l y . .
They are both accelerating at 9 . 8 m/s 2 . Therefore, when the hero jumps out of the building (which you shouldn't do, anyway), the villain will be going faster than him. In fact, until they both hit terminal velocity, the villain will be going faster than him.
If the hero wants to catch the villain, he must wait until the villain hits the ground with a splat.