Relativistic Particle in Magnetic Field
Consider a charged particle ( + Q ) of rest mass m projected from the origin of the X-Y plane with a velocity V i n i t at time t = 0 . The particle's motion is influenced only by a constant magnetic field B . Compute the distance of the particle from the origin at time t = 2 π .
Note:
-
Q = m = c = 1 .
-
V i n i t = 0 . 5 i ^
-
B = − B o k ^ , B o = 1
-
c is the speed of light.
-
V is the instantaneous velocity vector of the particle.
-
The force experienced by a charged particle due to a magnetic field is: F = Q ( V × B )
-
This problem most-probably requires numerical integration.
-
i ^ , j ^ , k ^ are unit vectors along the X, Y and Z axes respectively.
-
For a relativistic particle, its linear momentum is defined as:
p = c 2 − ∣ V ∣ 2 m c V
Bonus: Compare the trajectory of the particle with the non-relativistic case and perform this comparison for different initial speeds (between 0 and 1) along the positive X-axis. Comment on the observations.
The answer is 0.4718.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
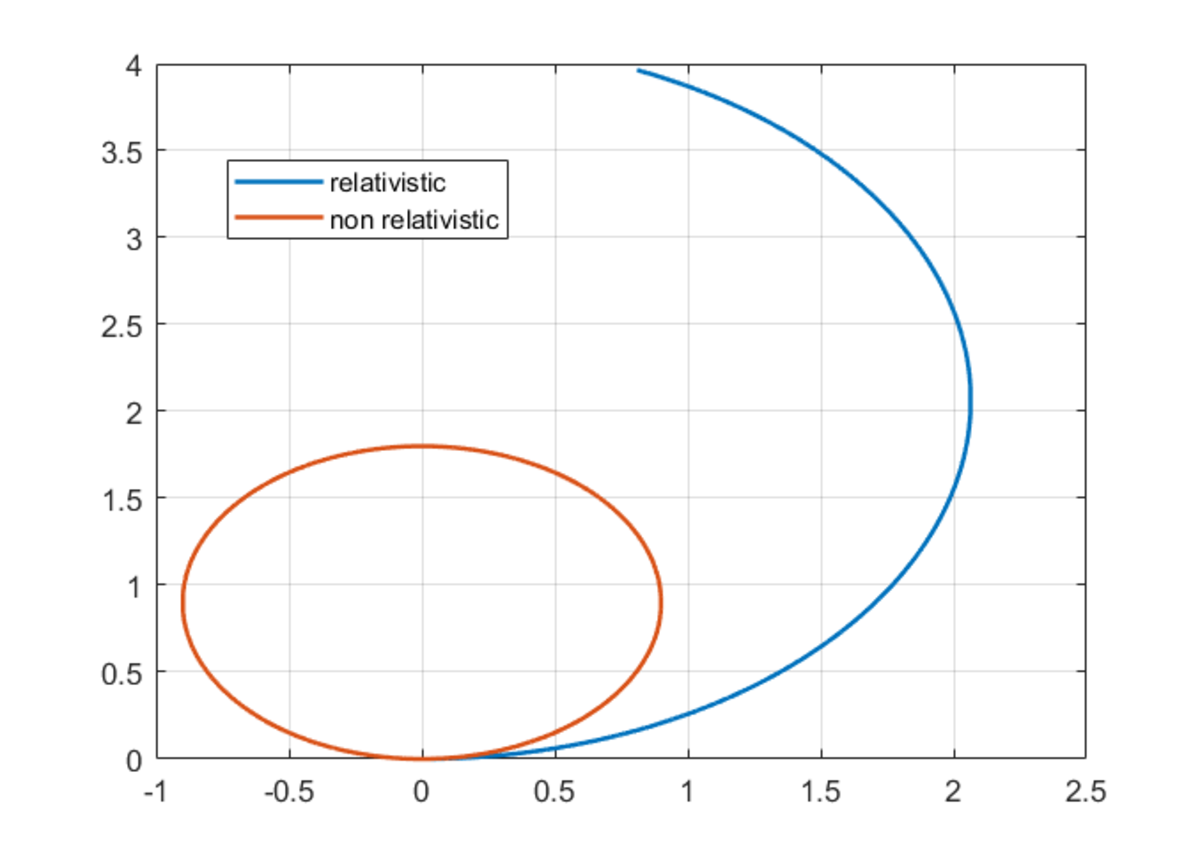
That's a nice way of doing it. Intuitively, you would expect the particle to be "more massive" at relativistic speed, thus traveling along a larger circle. And that is indeed what we see.
Log in to reply
Thanks. Additionally, at all instants of time, the speed of the particle remains constant. This property is consistent with the non-relativistic case.
Log in to reply
I get the constant speed as well. The discrepancy on this one is still bugging me
Log in to reply
@Steven Chase – I understand that feeling. The only major difference that I see in our approaches is the fact that you employed the use of numerical differentiation. What I can do, a little later in the day, is to try solving this problem using your approach and see if I can reproduce the results you obtain. If so, then we know for sure that the discrepancy is caused by the numerical derivative.
Log in to reply
@Karan Chatrath – The thing is, my speed is constant as well, so it seems that the whole term is irrelevant, including the numerical derivative. But thanks for checking. Here's another line of argument which I think is interesting:
1) Start with my second equation (I can't imagine any mistake there)
2) Suppose we take it for granted that the speed is constant
3) In that case, the second numerator term drops out, and we are left with the classic Newton's 2nd law, simply with a modified mass
Log in to reply
@Steven Chase – You make a valid point. In fact, I ran a quick simulation with your latest comment in mind and what I see is that the result I obtain agrees with the observations that I have reported. This makes me more thoughtful about the discrepancy. I want to get to the bottom of it. I will let you know if I come up with a reason.
Log in to reply
@Karan Chatrath – Sounds good, thanks. I'll go to bed soon, but I'll check back tomorrow.
Log in to reply
@Steven Chase – @Steven Chase For what purpose??
@Steven Chase – So I just executed your code with the slight modification of dropping the terms 'mult1*vx' etc. in lines 70, 71 and 72. I get the result of 2.356 for the 0.8 case.
In the relativistic case for initial speed v = 0 . 8 , do you end up with a final distance of 0 . 9 1 2 ? My implementation seems to work fine for 8 0 % SOL.
Log in to reply
Unfortunately not. I end up with a result of ≈ 2 . 3 5 6 . Checked at time steps 1 0 − 5 s and 1 0 − 6 s .
This was a cool problem. I initially started off well, but took some lazy shortcuts that hampered my progress. I have since revised the solution. For the relativistic case, F = m a no longer applies. Rather, the following holds:
F = d t d p
We are given the expression for the relativistic momentum. Using the quotient and chain rules of differentiation results in:
F = c 2 − v 2 c 2 − v 2 m c d t d v − v m c 2 1 ( c 2 − v 2 ) − 1 / 2 ( − 2 v d t d v )
Make use of the following relationship:
d t d v = v v ⋅ a
Resulting in:
F = c 2 − v 2 c 2 − v 2 m c d t d v + m c v ( c 2 − v 2 ) − 1 / 2 ( v x a x + v y a y + v z a z ) F = α d t d v + β v ( v x a x + v y a y + v z a z ) α = c 2 − v 2 m c β = ( c 2 − v 2 ) 3 / 2 m c
Splitting into individual vector components:
F x = α a x + β v x ( v x a x + v y a y + v z a z ) F y = α a y + β v y ( v x a x + v y a y + v z a z ) F z = α a z + β v z ( v x a x + v y a y + v z a z )
This results in the following linear system, expressed in matrix form:
⎣ ⎡ F x F y F z ⎦ ⎤ = ⎣ ⎡ α + β v x 2 β v y v x β v z v x β v x v y α + β v y 2 β v z v y β v x v z β v y v z α + β v z 2 ⎦ ⎤ ⎣ ⎡ a x a y a z ⎦ ⎤ α = c 2 − v 2 m c β = ( c 2 − v 2 ) 3 / 2 m c
From here, we can invert the matrix on each time step to solve for the accelerations, and solve numerically. One thing I think is very interesting here is that apparently in special relativity, the acceleration along one axis depends on the forces along all three axes. At low speeds v < < c , α ≈ m and β ≈ 0 (in the actual world, for example). Consequently, the matrix relating the accelerations to the forces is a pure diagonal matrix at low energies, which reproduces the classic Newtonian equations. So the de-coupled Newtonian equations we are familiar with are actually just a low-energy limit of the fully-coupled relativistic behavior.
Thank you for the solution. I just have one comment, however. I do not get the same result as you do for 0.9 case. Simulating till t = 2 π gives me the following:
Log in to reply
The convergence test results with varying time step are solid at v = 0 . 5 , but I'm getting singularities and numerical problems for v = 0 . 9 . Maybe the explicit Euler method is failing at high relativistic speeds.
Log in to reply
I have shared my solution as well. In contrast with your approach, I did not run into convergence issues. Hope you find it interesting.
@Karan Chatrath this graph is very accurate and beautiful. In which tool you make this type of graph??
Log in to reply
I use MATLAB
Log in to reply
@Karan Chatrath – @Karan Chatrath Sir Can i use MATLAB in my phone. I have Redmi note 7 pro??
Log in to reply
@A Former Brilliant Member – Unfortunately, you cannot.
I have significantly revised my solution, with a nice general result. My numerical results now match yours. I think it's very interesting that the accelerations are fully coupled to all three force components in general, and that the de-coupling we are familiar with is just a low-energy limit. It would be fun to do a relativistic problem with more involved dynamics, now that the fundamentals are taken care of. Thanks for your input.
Log in to reply
You're welcome. I'm glad the input was useful. I will think of more problems based on special relativity in the coming days.
Also, thanks for the updated solution and new insights. The fact that the accelerations are coupled is the reason why a system governed initially by linear nonrelativistic dynamics now becomes nonlinear. I think that this inherent nonlinearity increases the possibility for us to see some weird behaviour in different systems. This will be fun.
@Steven Chase has already provided a detailed solution with plots. I am sharing an outline of my solution as well as our approaches to the problem differ.
Consider:
F = Q ( V × B ) V = v x i ^ + v y j ^
This simplifies to:
F x = − v y F y = v x
Now:
p = p x i ^ + p y j ^
p x = 1 − v x 2 − v y 2 v x p y = 1 − v x 2 − v y 2 v y
Now:
F x = d t d p x = ∂ v x ∂ p x v ˙ x + ∂ v y ∂ p x v ˙ y = m 1 1 v ˙ x + m 1 2 v ˙ y F y = d t d p y = ∂ v x ∂ p y v ˙ x + ∂ v y ∂ p y v ˙ y = m 2 1 v ˙ x + m 2 2 v ˙ y
The partial derivative computations have not been shown here. This implies:
[ F x F y ] = [ m 1 1 m 2 1 m 1 2 m 2 2 ] [ v ˙ x v ˙ y ]
This implies:
[ v ˙ x v ˙ y ] = M − 1 [ F x F y ] M = [ m 1 1 m 2 1 m 1 2 m 2 2 ]
Finally, the equations of motion read:
[ v ˙ x v ˙ y ] = M − 1 [ − v y v x ]
From this point onwards, I performed numerical integration as follows. For the 0.9 case, I did not observe any convergence issues. Hope the code is readable. Please let me know if not.