Resistive Möbius Network
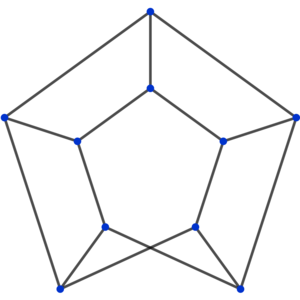
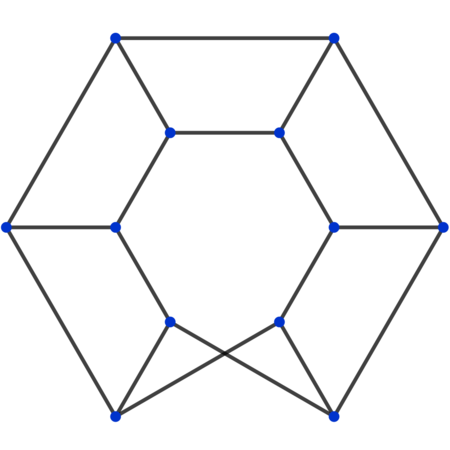 Consider a ladder-like network of
2
n
nodes (and
3
n
branches) in which the extreme nodes are connected with a twist. The given figures, for example, shows the topology for
n
=
5
and
n
=
6
. Each branch of the network consists of a
1
Ω
resistor. Let
R
n
denote the effective resistance between any two adjacent side nodes in the network. Evaluate the expression for
R
n
in terms of
n
and then find
n
→
∞
lim
R
n
.
Consider a ladder-like network of
2
n
nodes (and
3
n
branches) in which the extreme nodes are connected with a twist. The given figures, for example, shows the topology for
n
=
5
and
n
=
6
. Each branch of the network consists of a
1
Ω
resistor. Let
R
n
denote the effective resistance between any two adjacent side nodes in the network. Evaluate the expression for
R
n
in terms of
n
and then find
n
→
∞
lim
R
n
.
If the limit is equal to B ( C + D ) A for coprime positive integers A , B , C , D , then submit A + B + C + D .
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I didn't simplify the circuit and it got very messy. First, this is my sketch:
https://imgur.com/a/jqTYzKL
Current is neither created, nor destroyed. Therefore we get a couple of equations, regarding currents, flowing in different wires. They can be summarized: J k = ⎩ ⎪ ⎨ ⎪ ⎧ I + I 1 − I A 1 = I 2 + I B 1 , k = 1 I A k − 1 − I A k = I B k − I B k − 1 , 2 ≤ k ≤ n − 1 I 1 − I B n − 1 = I A n − 1 + I 2 − I , k = n Let V k and φ k denote the potentials of the k − t h outer and inner node respectively. Considering the potentials and Ohm's law, we get: J k R = V k − φ k I A k R = V k − V k + 1 I B k R = φ k − φ k + 1 I 1 R = φ n − V 1 I 2 R = φ 1 − V n Now using J k = I A k − 1 − I A k , J k = I B k − I B k − 1 and the above relations, we deduce: φ k + V k − 1 − 3 V k + V k + 1 = 0 V k + φ k − 1 − 3 φ k + φ k + 1 = 0 , Solving this system of recursive equations, I got: V k + 2 − 6 V k + 1 + 1 0 V k − 6 V k − 1 + V k − 2 = 0 This yields: V k = A α k + B α − k + C with α = 2 + 3 . I chose C = 0 for simplicity, as it doesn't change the potential difference across any two nodes. But substituting back up, I got φ k = − V k which was surprising (I see that @Mark Hennings got the same result)! The boundary conditions (outer nodes 1 and n ) gave: A = I R 8 α n − 2 − 8 α 2 − n − 1 5 α n − 1 + 1 5 α 1 − n − α n − 3 + α 3 − n + 2 α − 1 − 2 α 5 α − 1 + 5 α − n − α − 2 − α 1 − n B = I R 8 α n − 2 − 8 α 2 − n − 1 5 α n − 1 + 1 5 α 1 − n − α n − 3 + α 3 − n + 2 α − 1 − 2 α − 5 α − 5 α n + α 2 + α n − 1 And finally I got: R n = I V 1 − V n = R 8 α − 2 − 8 α 2 − 2 n − 1 5 α − 1 + 1 5 α 1 − 2 n − α − 3 + α 3 − 2 n + 2 α − 1 − n − 2 α 1 − n 1 0 α 1 − 2 n − 1 0 α − 1 − 2 α − 1 − n + 2 α 1 − n − 2 α 2 − 2 n + 2 α − 2 As n → ∞ this simplifies to: R n = R − 1 5 + 8 α − 1 − α − 2 − 1 0 + 2 α − 1 = 3 − 1 Any idea what I did wrong will be appreciated. Thanks in advance! Edit: Could it be that checking with k = 1 and k = n is incorrect? If so, how can I take into account the boundary conditions?
Log in to reply
It looks to me like your first two equations do not account for the Mobius twist. You have an inner n -gon and an outer n -gon, and the k th vertex of the inner ring is connected to the k vertex of the outer ring.
Log in to reply
I updated my first comment, have a look at it.
Log in to reply
@Veselin Dimov – After substitution k → k − 2 your new recursive relation is of 4'th order, so its general solution should contain four constants. The characteristic polynomial is Q ( z ) = z 4 − 6 z 3 + 1 0 z 2 − 6 z + 1 = ( z − 1 ) 2 ( z − α ) ( z − α − 1 ) ⇒ V k = A α k + B α − k + C + k D , 3 ≤ k ≤ n − 2 As far as I can tell you are missing the boxed linear term. It corresponds to − 2 n j I R in Mark Henning's solution for V j .
Edit: You may set C = 0 arbitrarily, but the remaining constants are still defined by the two initial and two final conditions V 1 , V 2 , V n − 1 and V n . One of the four conditions will be redundant as a result of setting C = 0 , of course, so you end up with a 3x3 system of equations.
I'm not sure how you managed to solve for A , B with the missing constant D - you should have encountered a contradiction somewhere along the way! Maybe you missed the fact your recursive relation is only valid for 3 ≤ k ≤ n − 2 and ignored the conditions for V 2 , V n − 1 ?
Great job actually finding an explicit expression for R n ! I only considered the symmetric case n = 2 N you can analyse with only half the network to get rid of that Möbius-twist. Repeated Delta-Wye-Transform on one of the half-networks does the rest, but only yields the limit, not the actual expression for R n .
By the way - A , B , C , D are most definitely not coprime...
Edit: Yes, they actually are coprime (even though not pairwise)... silly mistake of mine!
Log in to reply
Yes they are... There is no integer greater than 1 that divides them all. On the other hand, they are not pairwise coprime.
Log in to reply
My silly mistake, I misread the condition as "pairwise coprime". You're right! A classic reminder of "RTFM" - or "Lesen heßt Lösen", the German equivalent ...
Suppose now that the voltage at the vertex j is V j , for 1 ≤ j ≤ 2 n . Then we have V 2 n − V 1 V j − V j + 1 V j − V n + j = R I 2 n = R I j = R J j 1 ≤ j ≤ 2 n − 1 1 ≤ j ≤ n and so R K = R I j + R I n + j V j + 1 + V n + j + 1 = V j − V j + 1 + V n + j − V n + j + 1 = V j + V n + j − R K for 1 ≤ j ≤ n − 1 , and hence V j + V n + j = A − j R K 1 ≤ j ≤ n for some constant A . Since R K − R I = R I n + R I 2 n = V n − V n + 1 + V 2 n − V 1 = ( A − n R K ) − ( A − r K ) = − ( n − 1 ) R K we deduce that K = n I , so that (without loss of generality, we can choose A = 0 ) I j + I n + j = { n 1 I − n n − 1 I 1 ≤ j ≤ n − 1 j = n V j + V n − j = − n j I R 1 ≤ j ≤ n Solving the equations V j − V n + j = R J j and V j + V n + j = − n j I R for 1 ≤ j ≤ n simultaneously gives V j = 2 1 R ( J j − n j I ) V n + j = − 2 1 R ( J j + n j I ) 1 ≤ j ≤ n Another round of substitution into the given equations yields V j + 1 − 4 V j + V j − 1 = − n j I R 2 ≤ j ≤ n − 1 Solving this recurrence relation, there must be constants P and Q such that V j V j + n R J j = P α j + Q α − j − 2 n j I R = − P α j − Q α − j − 2 n j I R = 2 ( P α j + Q α − j ) for 1 ≤ j ≤ n , where α = 2 + 3 . Since R J 1 R J n = I R + V 2 n − 2 V 1 + V 2 = V n − 1 − 2 V n + V n + 1 we can solve a pair of simultaneous equations to obtain P , Q . If we do this. we obtain that the effective resistance of this circuit is R n = I V 1 − V 2 n = 6 1 ( 6 − 3 + 1 + ( 2 + 3 ) n 2 3 − n 3 ) R Putting R = 1 , we deduce that n → ∞ lim R n = 6 1 ( 6 − 3 ) = 2 ( 6 + 3 ) 1 1 making the answer 1 1 + 2 + 6 + 3 = 2 2 .