Resistors - 2
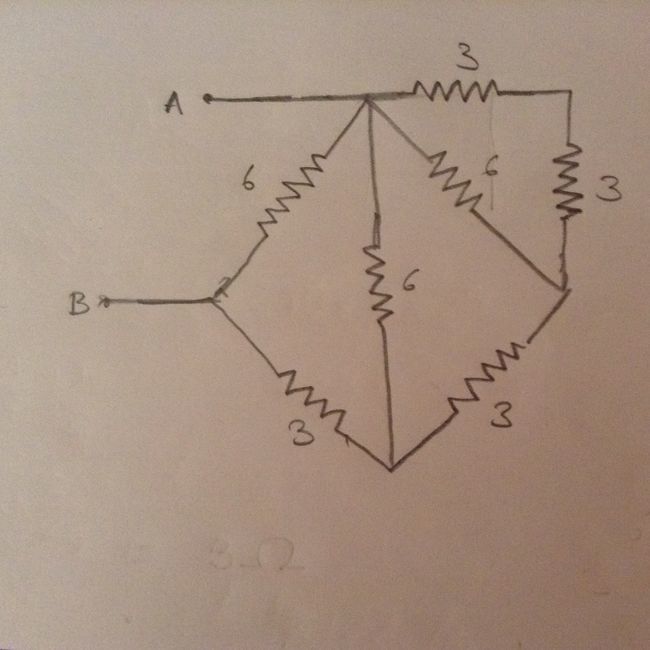 Find the equivalent resistance across A and B.
Find the equivalent resistance across A and B.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The connection though looks complicated, but it is very easy,
Let's start from A , we have two 3 Ω resistors in series, (let this be R 1 ), which is connected to a 6 Ω resistor in parallel (let this be R 2 ), therefore, the equivalent resistance is given by R e q 1 = R 1 1 + R 2 1 = 3 + 3 1 + 6 1 = 6 2 O r , R e q = 3 Ω
Similarly, we find that the remaining give rise to the same pattern, therefore, the total resistance of the conductor, i.e R t o t a l = 3 Ω
How the value of 1/R2 has been arrived to 16 and finally to 2/6 is not clear? Please clarify to reach to conclusion of R equivalent to 3 ohms ,Thanks!
Log in to reply
Thanks for pointing that out, it was a typo! ⌣ ¨
Log in to reply
Good that you realised that others are really interested in solution of the brilliant problems. Hope some one comes with the perfect solution,best wishes !!!
OH isee now
There is a catch and the answer is 12 ohms
Start form th point from where u don't have any branching u will solve it mentally I bet.
( ( ( ( 3 - 3 ) || 6 ) - 3 ) || 6 ) - 3 ) || 6 )
from uppermost right corner, 3+3=6, 1/(1/6+1/6)=3, 3+3=6, 1/(1/6+1/6)=3, 3+3=6, 1/(1/6+1/6)=3
In the rightmost top corner, the two 3 ohm resistors are connected in series with each other and their combination ( 3+3=6 ) is connected in parallel with the 6 ohm resistor. Hence the total resistance of the right top corner is 6 || 6 = 3 ohm. This 3 ohm is connected in series with the lowermost right 3 ohm resistor giving effective resistance of 3 + 3 = 6 ohm. This 6 ohm is again connected with the central 6 ohm resistor in parallel giving resistance 6||6=3 ohm. This 3 ohm is now in series with the lowermost left 3 ohm giving total as 3+3=6 ohm. Now this 6 ohm is connected in parallel with the 6 ohm resistor between points A and B giving total effective resistance between A and B as 6||6=3 ohm... That's it...
3+3=6,6||6=3,3+3=6,6||6=3,3+3=6,6||6=3
The two 3 Ω resistors in the top right corner are in series therefore total resistance of the two is 3+3=6.
These resistors are also in parallel with the 6 Ω resistor in the top right corner of the rhombus like arrangement of the resistors, therefore the total resistance will be- 1/(1/6+1/6)=1/(2/6)=6/2=3 Ω .
This 3 Ω is in series with the 3 Ω in the bottom right corner and total resistance will be=3+3=6.
This 6 Ω will be in parallel with the 6 Ω in the center and as we have seen above the total resistance will be 3 Ω .
This 3 Ω is in series with the 3 Ω in the bottom left corner so the total resistance of the two will be 3+3=6 Ω .
This 6 Ω is in parallel with the 6 Ω in the top left corner and thus the total resistance will be equal to 3 Ω .