Retrograde problem 1
In the following position, the color of each piece is unknown (each piece could either be white or black), but it is known that the position arose from a series of legal moves, starting at the usual starting position.
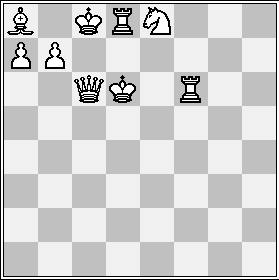
Before the last move was made, Black had a pieces worth b points (on the scale Queen = 9, Rook = 5, Bishop = Knight = 3, Pawn = 1, King = 0). What is the product of a and b ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Why cant the black piece on d8 be a bishop?
Log in to reply
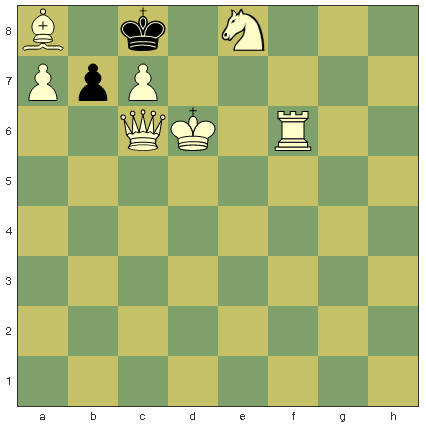
Consider this as the previous set up before the current position (omitted the piece on d8 for clarity)
Note that the King on c8 could not have been on b8 in the previous move as that would be a double check from pawns. And also, the pawn is on it's base square and hasn't moved. So essentially, whichever piece black has on d8 had to be a part of the previous move. If it was a Bishop, the only possible square it could've come from is e7. But in e7, the white king would be in check, meaning the white king put itself in check in it's previous move, which is not legal. Only a knight from e6 could have come to d8 without the previous move being illegal.
Log in to reply
How did white Bishop get to a8 if B7 was always there?
Before the last move, Black had 3 pieces. A king, a pawn and a knight.
The only possible valid last move was a discovered double check.
Perhaps the reader would prefer to work out the rest of the details.
Two cases. 1). The black king is on c-file(c8). He is under check by the white pawn on b7. Meaning pawn moved to that position on the last move and the Queen and rook are also checking the black king. 3 checks in 1 one move. Not possible! Meaning the king on c8 is white and not black. 2). If black king was on d6, then 2 rooks and the Queen are checking him. In one move or say even two half moves, how can such a position arise?
Log in to reply
In case 1). If the black king is on c8, then the pawn on b7 is black.
I can think of a way a white bishop could have gotten to a8 in this case, can you?
Log in to reply
No I did write that the pawn on b7 has to be white. But why doest it have to be that if black king is on c8, then white pawn cant be on b7? The more likely thing to have moved on the previous move was the white pawn to b7. Also the black king is simultaneously under check from three pieces. Not possible even with a double discovered check. Now even if the black king was on d6 he would still be under check from three sources, 2 rooks and the queen. Now this queen is right beside him! Not sure how you can triple discover this check.
Log in to reply
@Siva Bathula – You are correct that the black king cannot be on d6, there are too many checks and no way to get there.
The black king must be on c8, and therefore the pawn on b7 must be black or there are too many checks.
White moved last, the move was a capture causing a discovered double check. There were a couple of pawn under-promotions to pieces other than a queen to allow this to happen. The conditions for this don't have to be likely, just possible.
I hope I have given enough clues for you to work it all out now. Have fun!
Log in to reply
@Steven Perkins – If the pawn on b7 is black then there is no way that either coloured light squared bishop can ever reach a8. The only way a light squared bishop can reach a8 is if there ever was a hole on b7. If the initial black pawn on b7 moves it can never come back there neither can any other black pawns. So the pawn on b7 has to be white. Then the black king on c8 was in check, and triple check again? So not possible.
Now the underpromotion you mentioned was the pawn on c7 to kill a black piece on d8 to promote to white rook. But this case is invalid as well as I proved above.
Log in to reply
@Siva Bathula – I mentioned a "couple" of under-promotions. One of them was to obtain the bishop on a8. That's the only way the rest of the position is possible. That allows a black pawn on b7, and the pawn on a7 is therefore white because the black pawn had to be gone to allow the promotion to bishop.
The other under-promotion caused the double check. A pawn on c7 captured a black piece on d8 and choose to become a rook as you already mentioned. Now this case is valid, since the black king isn't in check from a white pawn.
Hope that helps!
Log in to reply
@Steven Perkins – You are right. Now it all makes sense. I was always fixated on that bishop being the regular one, didn't consider the promotions on a file.
First I realize that the pawn in (1,6) should be white, otherwise the bishop cannot be in (0,7).
Then without other revealing, you can easy match the value of pieces with the possible answer and the only valid options is 12, for 2 pieces with total value 6
Given the position of the two kings, and the rooks and queen, is it possible to double check one of the kings? I think it's no. 2 pieces for black? Not counting the king himself as a piece then.
Log in to reply
It seems clear the king counts as a piece, since it was given a point value. My solution takes this into account.
Note that either one of the kings are in double check at the moment, so the previous move had to be a discovered check of some sort. At first it seems impossible to get a double check from a previous position, but considering the rules of promotion helps find the last move.
Since Qc6 and Rd8 are double checking either Kc8 or Kd6, we can say they are both of the same color. From observation it is clear that Rd8 wasn't a part of the board the last move and was promoted from a pawn on either c7,d7, or e7. But if the pawn was on d7 or e7, Kc8 would be in check, which is not possible. Hence, there was a pawn on c7, and we can conclude there existed some piece on d8.
From this we can conclude that Qc6, Rd8 (Previously c7) and Kd6 are white while Kc8 is black.
Now to allow white to make the move c7xd8=R+, there should've been no other checks in the previous move. Hence Rf6 and Ne8 are white while b7 is Black. Since the board is oriented with white starting at the bottom (evident from the promotion), we can say there is no way for a bishop to land on a8 unless it was a white bishop, promoted from an a7 pawn, and hence the pawn on a7 right now should also have been white.
And finally the black piece on d8 in the previous move had to be a knight, since if it was either a rook, bishop or queen, the King on d6 could not move to this position.