Revenge of the progressive Sangaku
Professor Michael Mendrin challenges Chew-Seong Cheong and David Vreken to solve a tricky problem:
-
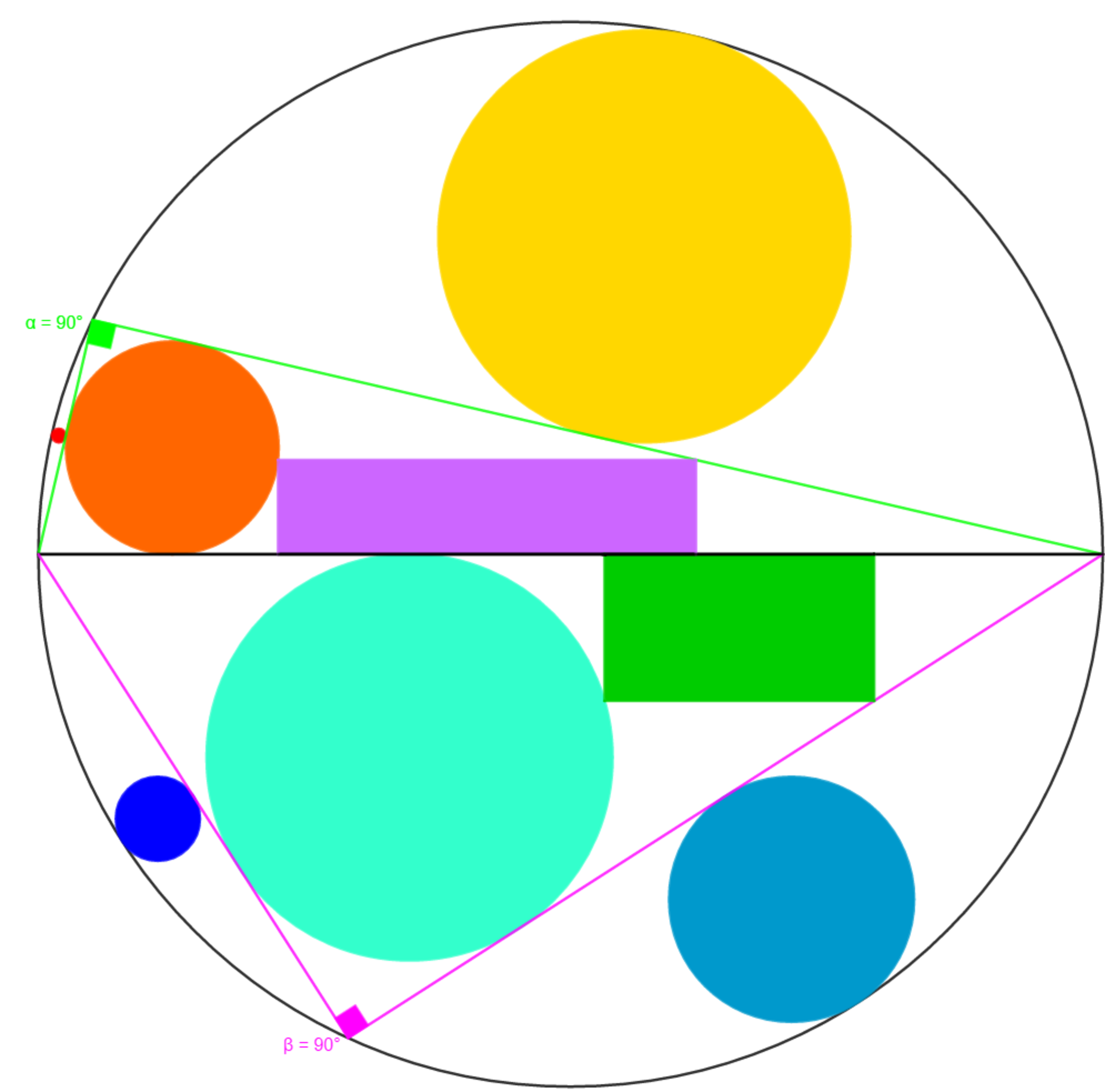
He draws a cirlce of radius 1 and divides it into two semi-circles. David Vreken shall use the upper semi-circle and Chew-Seong Cheong shall use the lower semi-circle.
-
Then he asks them to place a point on their respective semi-circle so that they can draw a right triangle with the hypotenuse being the circle's diameter, thus creating 2 circular segments per semi-circle. Finally they need to draw the incircle of their triangle and the biggest circle they can inscribe in each circular segment.
-
Easy, right? But there is a twist ! The radii of David's and Chew-Seong Cheong's circles need to be in a different arithmetic progression.
-
After doing so, Professor Michael Mendrin asks them to inscribe the largest (in terms of area) possible rectangle in their respective triangle so that the rectangle is tangent to the triangle's incircle.
- The question : Either David Vreken or Chew-Seong Cheong constructed the three circles whose sum of areas is smaller. This sum of areas can be calculated and the result can be expressed in its simplest form as b a π
- One of the two contestants could draw a rectangle larger than the other's, we denote its area : β
-
Evaluate
b
⌊
1
0
7
β
⌋
−
⌈
π
⌉
+
a
The answer is 13942.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wow, I'm honored! By the way, I think the 1 0 7 should be inside the floor function with β .
Log in to reply
Indeed i corrected it, thanks ! I wanted to feature one great problemist and two great solutionists. What approach did you use i'm curious
Log in to reply
My approach was similar to yours, except I used the x -coordinate of M as my variable x instead of the length of M C like you did, so some of my expressions look a little different (and to be honest more complicated). But most of the steps I used were the same as yours, though.
Log in to reply
@David Vreken – I'll post another problem soon, hopefully there will be possible solutions...
@Valentin Duringer Nice solution.. will post mine..
Nice one putting @David Vreken and Chew-Seong Cheong in (I can't mention him though...)
@Valentin Duringer , thanks for inviting to solve this problem. I have been put off long problem questions that was why I didn't solve your earlier problems. I couldn't come up with solution that is as accurate as yours. But nonetheless I got it done though less dramatically.
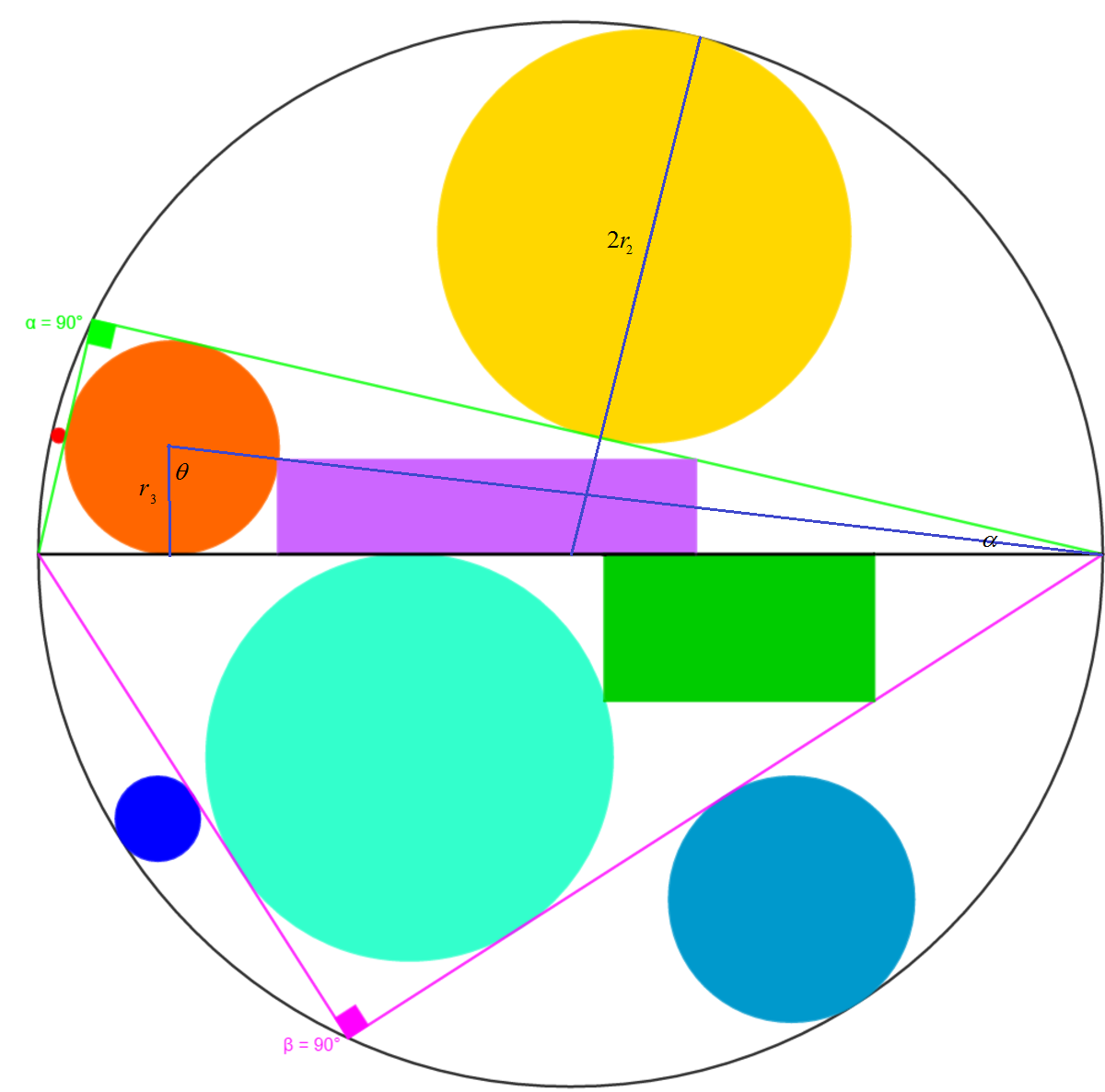
Let the radii of the small circle and big circle of the two circular segments be r 1 and r 2 respective. Let the measure of the smaller angle of the right triangle be α . Then we note that r 2 = 2 1 − sin α and r 1 = 2 1 − cos α . Let the inradius of the right triangle be r 3 . From semiperimeter × inradius = area of triangle , we have r 3 = 1 + sin α + cos α 2 sin α cos α . Since r 1 , r 2 , and r 3 are in an arithmetic progression, we have for the upper semicircle r 1 + r 2 = 2 r 3 and for lower semicircle r 1 + r 3 = 2 r 2 . Solving for the two α 's, we get:
Semicircle Upper Lower α 0 . 2 2 7 7 9 9 3 3 7 0 . 5 6 9 8 4 8 2 5 3 r 1 0 . 0 1 2 9 1 7 1 3 1 0 . 0 7 9 0 0 8 5 7 4 r 2 0 . 3 8 7 0 8 2 8 6 9 0 . 2 3 0 2 4 7 8 5 7 r 3 0 . 2 0 . 3 8 1 4 8 7 1 4 Area of 3 circles 0 . 1 9 π 0 . 2 0 4 7 8 8 8 6 8 π
Since the smaller sum of areas of three circles is 0 . 1 9 π , then a = 1 9 and b = 1 0 0 .
To find the area of the largest inscribed rectangle, let the measure of the angle extended at the incenter between the vertical and the point the corner of the rectangle touches the circle be θ . Then the area of the rectangle is given by:
A = r 3 2 ( 1 − cos θ ) ( cot 2 α − sin θ − cot α ( 1 − cos θ ) )
Solve for the θ that gives the largest area then calculate A max . We get:
Semicircle Upper Lower A max 0 . 1 3 9 1 4 8 0 6 6 0 . 1 3 9 4 1 8 5 0 8
Therefore β ≈ 0 . 1 3 9 4 1 8 5 0 8 and b ⌊ 1 0 7 β ⌋ − ⌈ π ⌉ = 1 3 9 4 2 .
Nice solution using angles ! I'll post a problem with excircles soon, i think there will be lots of possible approaches. The only issue is that i'm too slow creating problems.
Let us place a point M on the circle with diameter [AC], we obtain a right triangle AMC with A C = 2 , M C = x and M A = 4 − x ²
Now we will be able to express the radii of the three circles in terms of x . We denote R 1 the radius of the incircle of the right triangle AMC. We denote R 2 the radius of the circle tangent to (MC) and R 3 the radius of the circle tangent to (MA)
R 1 ( x ) = P e r i m e t e r 2 A r e a = 2 + x + 4 − x ² x 4 − x ²
We shall use the product of chords equality in a circle to express R 2 and R 3 in terms of x . Since the two circles inscribed in the circular segments are the largest possible, their centers are located on the perpendicular bisectors of [AM] and [CM] respectively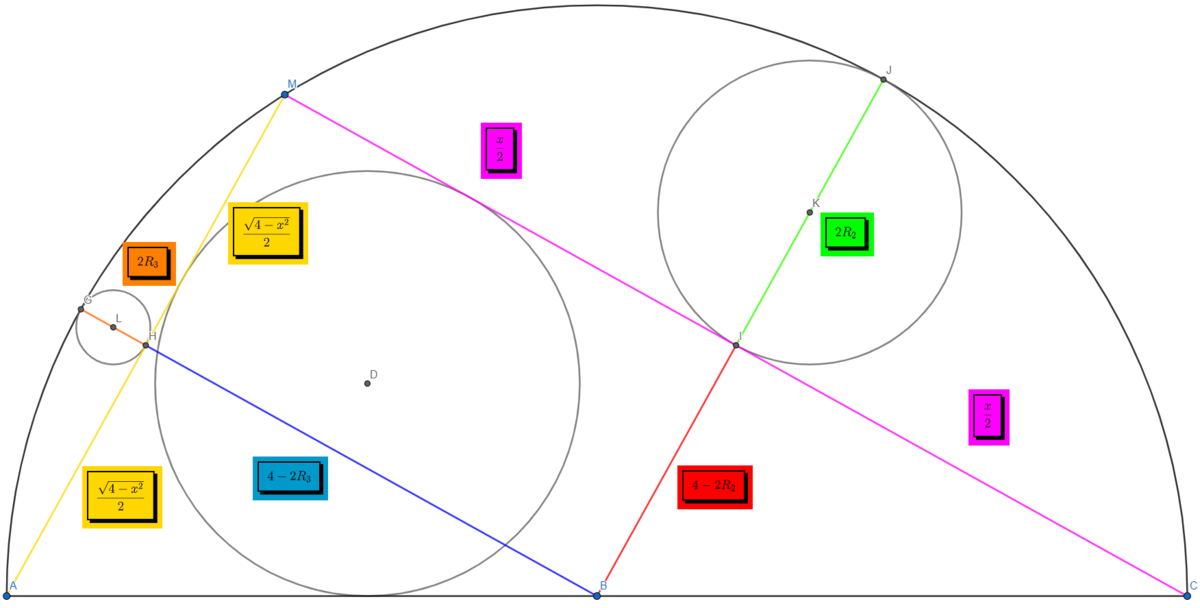
This gives us 2 R 2 ( 4 − 2 R 2 ) = 4 x ² <=> R 2 ( x ) = 4 2 − 4 − x ²
But we can also consider the possibility of the incircle not being the largest circle, this gives us R 2 − R 1 = k 2 and R 2 − R 3 = k 2 where R 2 > R 1 > R 3
We solve R 1 − R 2 = k 1 and R 2 − R 3 = k 1 in terms of x where R 1 > R 2 > R 3 , we find x 1 = 1 7 6 + 1 6 2 and k 1 = 3 4 1 0 2 − 9
We solve R 2 − R 1 = k 2 and R 2 − R 3 = k 2 in terms of x where R 2 > R 1 > R 3 , we find x 2 = 5 6 + 1 4 and k 2 = 1 0 2 7
After calculating R 1 , R 2 and R 3 for both possible values of x we find that the area of the three circles is smaller for x 2 and equals : 1 0 0 1 9 π
Now let's determine the area of each rectangle. One way to do it consists in drawing a coordinate system, the center of the incircle being the origin. Let's solve it for x 2 . We place a point W ( x ; y ) . The height of the rectangle will be 5 1 − y
Let's determine the length of the rectangle, the diagram below shows the different parts of the diameter, the first is determined using basic trigonometry in the triangle. The second part is equal to the x coordinate of point W, and since point W is on the circle with equation x ² + y ² − 2 5 1 = 0 , the length x can be expressed in terms of y, thus x = 5 1 − 2 5 y ² . Next we have the length of the rectangle. At last we use trigonometry to express the last portion of the diameter in terms of y , we get 2 5 − 6 1 4 1 1 ( 5 1 − y ) 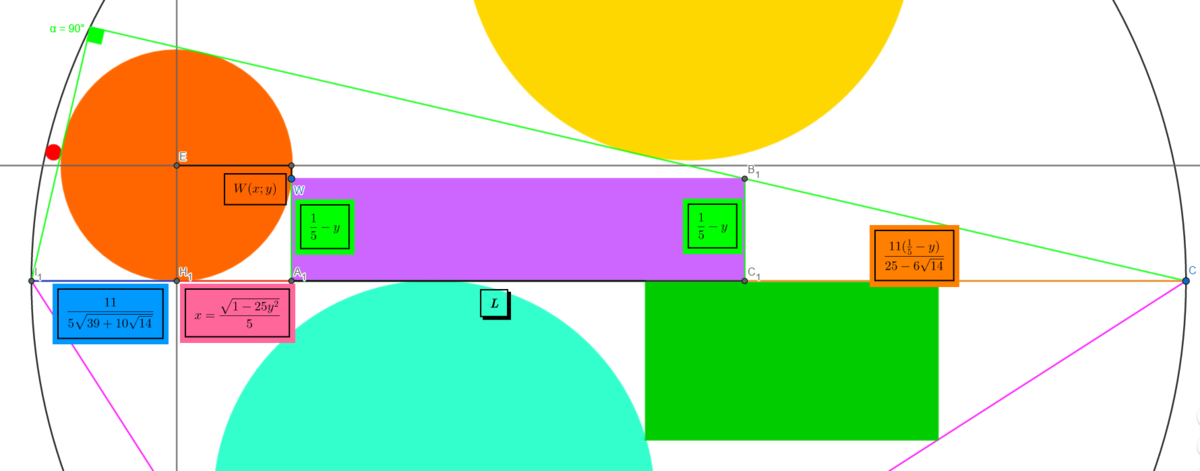
Since the diameter is 2, we find L = − 5 1 − 2 5 y ² − 2 5 − 6 1 4 1 1 ( 5 1 − y ) − 5 3 9 + 1 0 1 4 1 1 + 2
Now we express the area in terms of y A ( y ) = ( − 5 1 − 2 5 y ² − 2 5 − 6 1 4 1 1 ( 5 1 − y ) − 5 3 9 + 1 0 1 4 1 1 + 2 ) ( 5 1 − y )
The maximum of the function is 0 . 1 3 9 1 4 8 0 7 . . . . We use a similar method to solve the maximum area of the rectangle for x 1 and we find β = 0 . 1 3 9 4 1 8 5 1 . . . and this is the larger rectangle.
b ⌊ 1 0 7 β ⌋ − ⌈ π ⌉ + a = 1 0 0 1 3 9 4 1 8 5 − 4 + 1 9 = 1 3 9 4 2