Revision of C a p a c i t a n c e
Find the Capacitance of an isolated ball shaped conductor of radius R 1 surrounded by am adjacent concentric layer of dielectric with permittivity k and outside radius R 2 If your answer comes in the form of b + R 2 R 1 ( k − c ) a π ϵ 0 k R 1 Type you answer as a + b + c
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very impressive solution.
@Karan Chatrath sir the latest problem of E and M which is uploaded by Steven sir .
from last 2 days he is helping me in how to solve problem through python (solving integration and differential equations)
He has uploaded the latest problem in my request only that i will do that from python only.
but i am not able to solve .
here is my code ,please help ,i don't want his hard work to be blown up . He will feel happy if i upload the solution using python
Thanks in advance.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
Log in to reply
How do you want me to help exactly? Let me know and I will try. Because I don't want to just tell you the code. That will defeat the purpose of your learning. But generally speaking, I would do this:
- Declare a variable H = 0 for heat dissipated by resistance
- Start a while loop
- Solve for I ˙
- Apply Euler integration to obtain the current
- Compute the heat dissipated in that elementary time interval due to this current. Add it to H end while loop when t ≥ 3 π / 5
Log in to reply
@Karan Chatrath
i am taking help from previous RLC problem ,how to write a code .
btw can you tell ,what does ISmin = 999999.0 mean??
thanks in advance
Log in to reply
@A Former Brilliant Member – I cannot answer that question without looking at the code. If you share a link to that solution, then I will be able to answer that question.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir open this problem https://brilliant.org/problems/rlc-4-16-2020/
see the solution , in his 43rd line of code he has written that only.
thanks in advance
Log in to reply
@A Former Brilliant Member – He has initialised a variable to calculate the minimum current. It is set to a very high number, so at every time step when the instantaneous current is lower than the value of IS min, the lower value of current replaces the present value of IS min. It is a programming trick to find a minimum value of a function.
@A Former Brilliant Member – I don't know why you deleted the comments. Do not be discouraged. Please try your best to understand the way of coding instead of rushing to solve a problem. It is impressive that you are willing to learn. But my only suggestion is to learn it in a systematic way.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath @Karan Chatrath sir my code is not running,as it is obvious that it will be wrong
guide me ,what i should add more in this code .
btw when i go to run this code a orange line comes at the right (24th line) saying me invalid syntax.
below my code is attached .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
Log in to reply
@A Former Brilliant Member – Okay, I said I won't help but here you go. Good attempt..
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
|
@A Former Brilliant Member – Here is the thing. I have only used Python once or twice before in my life and I cannot say that I know that language. I usually use a different coding language. But I could still figure it out. This is because I have worked on the basics for a long time. I suggest that you do the same.
Log in to reply
@Karan Chatrath – @Karan Chatrath why you have used python so less?
Log in to reply
@A Former Brilliant Member – The coding language that you use matters less once you have strong fundamentals. I learned to program in other languages so I am more comfortable with those than I am with Python.
Log in to reply
@Karan Chatrath – @Karan Chatrath sir in which programming language you are more comfortable ?
Log in to reply
@A Former Brilliant Member – MATLAB at the moment.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir in this
Problem
at the solution's code
code line 33,34,35
what is the meaning of nx,ny,nz
thanks in advance
Log in to reply
@A Former Brilliant Member – Unit vector components.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir please provide me the code of this problem by using python(mid point theorem)
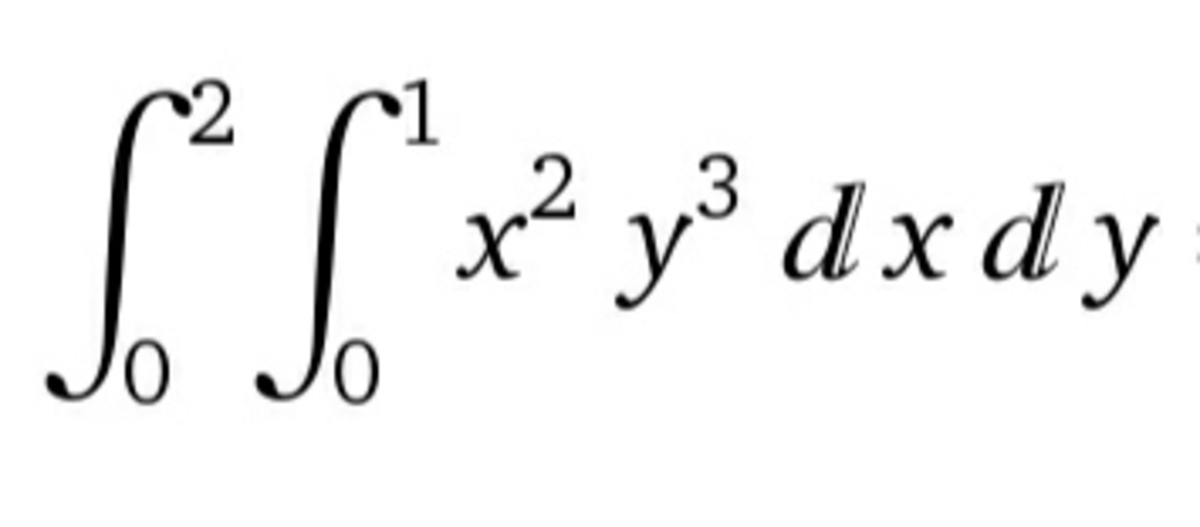
I have some question:
1)
Which is easy Matlab and python ?
I have noticed that codes of matlab are easy to write than in python?
2) Why does Matlab needs money to access, just like python why matlab company doesn't want to make it free. ?
3)
Can we solve integration in java also??
If yes , then why Steven sir always uses python ?
4) According to you what things I must learn in python which will definitely help me in future?
5)
I was running a code in my computer, it take me around 5 min to run
What should I do to reduce that time ??
Should I buy a more expensive computer?
Or attach something in my CPU??
6)
Which laptop is BEST for programming?
Which laptop do you have?
Thanks in advance
Hope I am not disturbing you.
Log in to reply
@A Former Brilliant Member – I gave you the code once. Show your attempt before asking for a solution.
Answers that I can give:
-
For me MATLAB is easier. In general, it depends on a user's comfort level with a language.
-
MATLAB offers more numerical tools apart from a coding environment. Those have commercial value. Python is only a coding environment.
-
Yes, Java can be used.
-
I answered this question in a comment that you deleted. Focus on understanding the syntax, looping and conditions (if-else, etc.)
-
I would not recommend spending money on expensive hardware. Avoid using very small time steps to make your program run faster. There is always a trade-off between speed and accuracy. Which one is more important depends on the problem and also depends on the programmer's preference.
-
There is no 'best' laptop. I think that whichever computer that you have is adequate.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir in this
Problem
While calculating the flux through disk ,we know that flux will be in
−
z
by knowing this why we are including terms of
x
and
y
??
i think we can make our code more smaller ??
am i correct??
Thanks in advance
The system is a series combination of two capacitors in the shapes of concentric spherical shells, one of inner radius R 1 , outer radius R 2 , electric permitivity k ϵ 0 , and the other of inner radius R 2 , outer radius ∞ , electric permitivity ϵ 0 . Their capacitances are C 1 = R 2 − R 1 4 π k ϵ 0 R 1 R 2 and C 2 = 4 π ϵ 0 R 2 respectively. Their equivalent capacitance is C 1 + C 2 C 1 C 2 = 1 + R 2 ( k − 1 ) R 1 4 π k ϵ 0 R 1 . So a = 4 , b = 1 , c = 1 and a + b + c = 6 .
Nice problem. Consider the geometry below:
This is the configuration of a spherical capacitor, the negative terminal of which is at infinity. The permittivities of each region is indicated in the diagram.
Let the charge on the innermost shereical conductor be Q . At any point on the red spherical region, the radially outward electric field due to the conducting sphere is:
E = 4 π k ϵ o R 2 Q
Let the electric potential at the surface of the conducting sphere be V i and that on the edge of the dielectrics be V o . To calculate the potential difference between these two surfaces:
E = − d R d V = 4 π k ϵ o R 2 Q
d V = − 4 π k ϵ o R 2 Q d R ∫ V i V o d V = ∫ R 1 R 2 − 4 π k ϵ o R 2 Q d R ⟹ V i − V o = 4 π k ϵ o Q ( R 1 1 − R 2 1 ) … ( 1 )
Performing the same steps to compute the potential difference between the edge of the dielectrics and the negative terminal of the capacitor:
E = − d R d V = 4 π ϵ o R 2 Q
d V = − 4 π ϵ o R 2 Q d R ∫ V o V ∞ d V = ∫ R 2 ∞ − 4 π ϵ o R 2 Q d R
⟹ V o − V ∞ = 4 π k ϵ o Q ( R 2 1 ) … ( 2 )
Adding (1) and (2) will give the potential difference between the terminals of the capacitor. After substituting and simplifying, that is:
V i − V ∞ = 4 π k ϵ o R 1 Q ( 1 − R 2 R 1 ( k − 1 ) )
Re-arranging and recognising that Q = C ( Δ V ) gives the required expression:
C = 1 − R 2 R 1 ( k − 1 ) 4 π k ϵ o R 1
Therefore: a = 4 ; b = c = 1