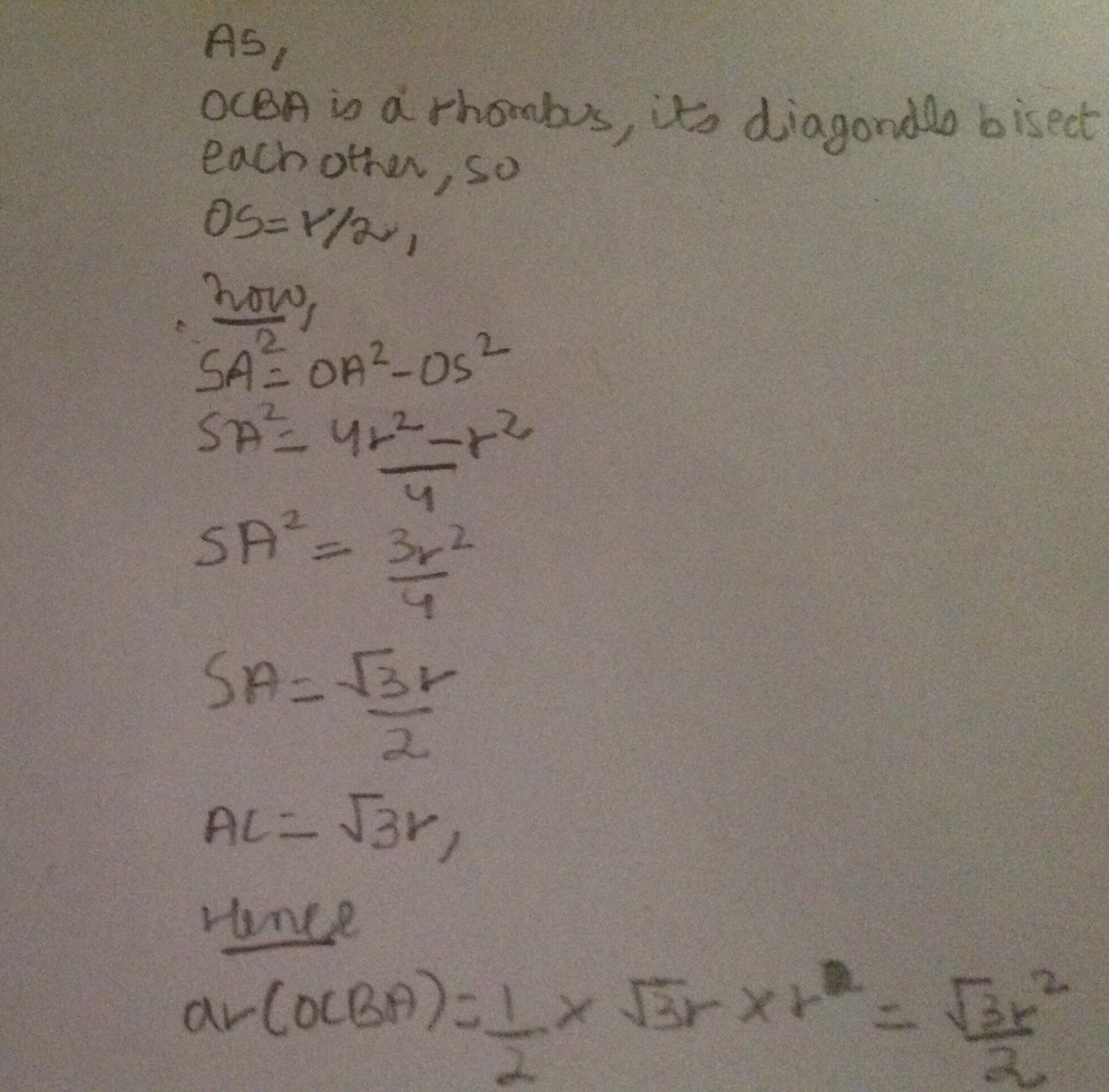A Rhombus Gets Cozy In A Circle

Geometry Level 1

A rhombus is inscribed in a circle with radius $r$ and center $O$ , such that one of the vertices lies on $O$ and rest lie on the circumference of the circle.

Find the area of the rhombus in terms of $r$ .

\dfrac{1}{2} r^2

\dfrac{\sqrt{3}}{2} r^2

4 r^2

\dfrac{\sqrt{2}}{2} r^2

3 solutions

Rishabh Sood
Feb 7, 2016

Desmond Yeung
Feb 14, 2016

It is quite obvious that the rhombus consists of 2 equilateral triangles of sides r units. By sine formula, area of each triangle is $\frac{1}{2}$ r²sin60°, which is $\frac{1}{4}$ * $\sqrt{3}$ r²

Therefore the answer is $\frac{1}{2}$ * $\sqrt{3}$ r²

You don't even need sin. You can use Pythagorean Theorem.

Jesse Nieminen - 5 years, 4 months ago

Can you explain more? I don't get your point.

Desmond Yeung - 5 years, 4 months ago

You have a right triagle which has an angle of 60 degrees. You can use Pythagorean Theorem to calculate its are without needing to calculate the value of sin 60 deg.

Jesse Nieminen - 5 years, 4 months ago

@Jesse Nieminen – Don't worry, there are many ways to solve this, I am just in 9th,so I don't know about the many other methods

Rishabh Sood - 5 years, 3 months ago

Harshendu Mahto
Feb 7, 2016

The correct answer is 3r^3 / 2 x r.

Kindly recheck your question....

Harsh an end u if you think that the answer is 3r^3/2×r, then for any value of 'r', the area of the rhombus, would exceed the area of the circle which is impossible. So, plz check your answer again.

Ashish Menon - 5 years, 4 months ago

Next time plz think twice before posting a solution. One example when $Prince$ $of$ $Morroco$ did not think twice before making choice of his $caskets$ , he did not win $Portia$

Anyone, agrees with me?

Ashish Menon - 5 years, 4 months ago

me! of course