
Riding a wave
Bella holds the end of a rope tied to a vertical wall. Point A is marked on the rope. She gives the rope a small flick to start a wave pulse, which travels towards the wall. At some instant, the rope with the wave pulse will look as shown below.
In which direction is the point A moving at this instant?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
To learn more about waves, check out the new Waves chapter in the Science Essentials course!
Waves Chapter

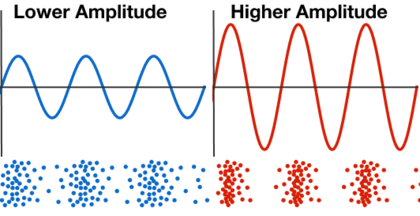
Amplitude
Build your understanding of wave properties such as amplitude and velocity.
Standing Waves
Explore standing waves—the waves responsible for the notes produced by many musical instruments.

Great analogy.
I'd never heard of what Americans call 'the wave' referred to as a 'Mexican wave.' https://en.wikipedia.org/wiki/Wave_(audience) offers an interesting history.
It kind of depends on whether point A is on the rope or on a projection of the rope against the wall. If we mean point A on the projection, it clearly moves toward the wall. If we mean on the actual rope itself, it moves up and a little bit toward the wall. At the start there were equal amounts of slack behind and ahead of point A. If point A was at the very midpoint of the a 10' rope and if the wave required an extra 1' of rope slack as shown in the picture, 6" was in front of point A and 6" was behind, meaning that point A is displaced 5' from the starting point of the wave but has 5' 6" of rope behind it and 5' 6" ahead of it. As the wave travels toward the wall, all of the slack moves but point A is now 5' 6" from the start meaning it moved 6" toward the wall and there is now 5' 6" of rope between point A and the wall, whose displacement distance is now 4' 6" from point A, with the full 1' of slack between point A and the wall.
To check our reasoning, rope segments started 10' plus 1' of slack making 11'. Displacement distances start 10' and end 10'. After the wave passes point A, rope distance is still 5' 6" behind point A and 5' 6" ahead of point A, making 11'. Displacement distances are 5' 6" behind point A and 4' 6" ahead of point A to the wall, making 10' total displacement.
Log in to reply
Exactly: it depends on the definition of what A is. And what's more: If it really is 'an instant' then that means it is as it were a photograph we're watching and in that photo A is not moving at all.
Log in to reply
Bingo that is my comment. They did not say point A was ON THE ROPE and as such it is just a point in space.I assume they are using the ground as their reference so a point A is not moving UNLESS it is on a moving object.
Log in to reply
@Jon Firor – The question does say that point A is marked on the rope.
A very nice explanation thank you for giving that explanation
In the image, point a is sitting precisely on the line of forward tragectory. The section of rope after point A (the negative gradient) is at its highest moment of deflection and will then proceed to move forwards and upwards, however; since the both the + and - gradients are at the highest point of deflection, at that exact moment, point A is not moving at all. The answer is in the question.
Log in to reply
I think point A is on an upward path toward the maximum height of the wave; I believe only the min/max points of the wave would be at rest.
I agree with Melanie. Point A in fact has the maximum speed. The points before A and the points after A both move upwards in that exact moment.
doesn't any point at an instant is at rest
Log in to reply
I agree - poor question wording ... there is no “Instantaneos” motion - velocity needs a time component. If we drop that word from the question then yes, upward is correct. Given current wording, “at rest” should be the correct answer.
Log in to reply
That way of thinking is outdated by a few millennia. Aristotle would agree with you. Modern physics does not.
Objects do have non-zero instantaneous speed, or else nothing would be moving. The instantaneous speed of an object is defined as the limit of the ratio Δ t Δ x as Δ t tends to zero.
Hey guys !
@Dhruva Sakhare , I had the same issue ! I was reasoning as greek philosophers used to do I was like "at a point there is no space, without space no motion is possible and without motion there is no speed so it's impossible to talk about speed for one point" but Newton put his b*lls on the table lol and told us that instantaneous velocity is the velocity of an object in motion at a specific point in time. This is determined similarly to average velocity, but we narrow the period of time so that it approaches zero (it APPROACHES zero, got it ?). So at a given instant, the point A isn't at rest at all it DOES have a velocity so it has a speed and a DIRECTION !
As @Pranshu Gaba said "Objects do have non-zero instantaneous speed, or else nothing would be moving. The instantaneous speed of an object is defined as the limit of the ratio Δx/Δt as Δt tends to zero." (Pranshu said TENDS TO, for anyone who would still get a problem with the 'instantaneous' stuff)
I also liked the answer of @Willem Monsuwe : "That way of thinking is outdated by a few millennia. Aristotle would agree with you. Modern physics does not."
So it's a question that's somewhat misleading then? (It wants you to assume it's talking about the wave itself, not the point on the string)
Log in to reply
The question says that point A is marked on the rope, so it is fixed with respect to the rope. The question is asking about the motion of A , which is just in the vertical direction.
I agree to Thomas Lippmans comment. A moves slightly towards the wall, as the wave form needs more rope than a straight line.
I disagree with the answer. As you can see from the picture of the duck, the motion of a given particle is not up and down, it is circular.
imagine a point on the rope 10 feet from the end attached to the wall. before the wave comes through, the point will be 10 feet from the wall. after the wave goes through, it will be closer than 10 feet from the wall because the rope is now "slack": part is above and part is below the horizontal and the rope has not changed in length.
in the current problem the wave is half way through. It has completed the "down" part of its journey, but has not reached its apex, so it will be moving "up". but only 1/2 the wave is between it and the wall: more "slack" will build between the point and the wall in each unit of time until the wave has fully passed, at which point it will be stationary, at its closest point to the wall. As the wave hits the wall and reflects, the process reverses
In the problem statement, it's unclear what Bella's original movement was; whether it was a flick upward or downward.
If it was a flick up, then the wave as shown has already reflected back from the wall and it's returning toward Bella in which case point A will move DOWN.
Vice versa if her original flick was first downward.
Think of the rope shifting through. For the wave to move forward the current point A must stay in the same position while the wave making it go up
They did not say point A was on the rope and as such point A is a fixed point in space and hence not moving. If we say the ground is not moving and use it as our reference and then pick any point A that is not on a moving object then of course it is stationary. This is the correct answer to the question as worded. Now if they said what direction is point A on the rope moving then the answer is upwards. The devil is in the details and they have posted the wrong answer as being correct.
Log in to reply
The puzzle, as stated, says "Point A is marked on the rope." How much more clear can that be?
That is not the correct answer. At that 'instance', thee is no transition of time. It is at a point in time that is fixed. Therefore it is not moving at that instance in time. For movement to occur there must be a transition in time over a period. The question needs t be rephrased to include possibly 'the direction the point A (on the rope) has been moving in the past (e.g) 1 millisecond.
Log in to reply
We can indeed define the speed of an object at a given instant. It is the limiting value of the ratio Δ t Δ x as Δ t tends to 0. You can read more about instantaneous rates of change in the average and instantaneous rate of change wiki.
Log in to reply
Pranshu Gaba, You stated 'tends' but not zero simply because zero is not possible for delta x within a sine wave?
I tend to agree with you, Ian. Instant or instantaneously means zero delta T. Therefore as you said "there is no transition of time which would be true. Take a square wave, for instance, it is not possible to produce straight vertical lines to a square wave they would have to travel at zero time. it does take time no matter how small to for the ramps. To observe this just look at a square wave with a high-end oscilloscope. Dial up any frequency and the vertical line will ramp up, not go from from one amplitude to another in zero time. It is tied to the laws of sines.
This is my way of reasoning anyway. The other comments seem contradictory to mine but make sense too.
How can a thing move at all in an instant? It has to be at least some line that defines A right? A line through time?
Log in to reply
If not it wouldn't have gone up or anywhere in that instant, I don't know the definition of an instant though maybe that just means a very small fraction of time or some shit
In an instant, the point has a velocity. This isn't a movie, in which everything stops moving so the camera can go around and show the scene from different angles; it's just an instant in time. Things are still moving at each instant.
Normally, wouldn't you flicker the rope up and then down? The drawing looks like she move the rope down first and then up, which may lead someone to believe it is a trick question and that the wave is currently moving back.
Log in to reply
That's exactly what I was thinking, which is why I almost said downwards. I reread the question, and studied the diagram, and saw no hint that the wave would reflect off the far wall and come back the other way... so I reluctantly said upwards and cringed as I clicked submit.
Thank you, Jon!
Even though the wave as a whole moves to the right, the particles on the rope only move up and down, like the people in a Mexican wave. The particles at A moves up as it takes the position of the particles that was behind it.