Ring Tension
A uniform circular ring hangs by a single point at its top, with gravity pointing downward. At what angle θ (in degrees, between 0 and 9 0 ) is the tension in the ring equal to the weight of the ring?
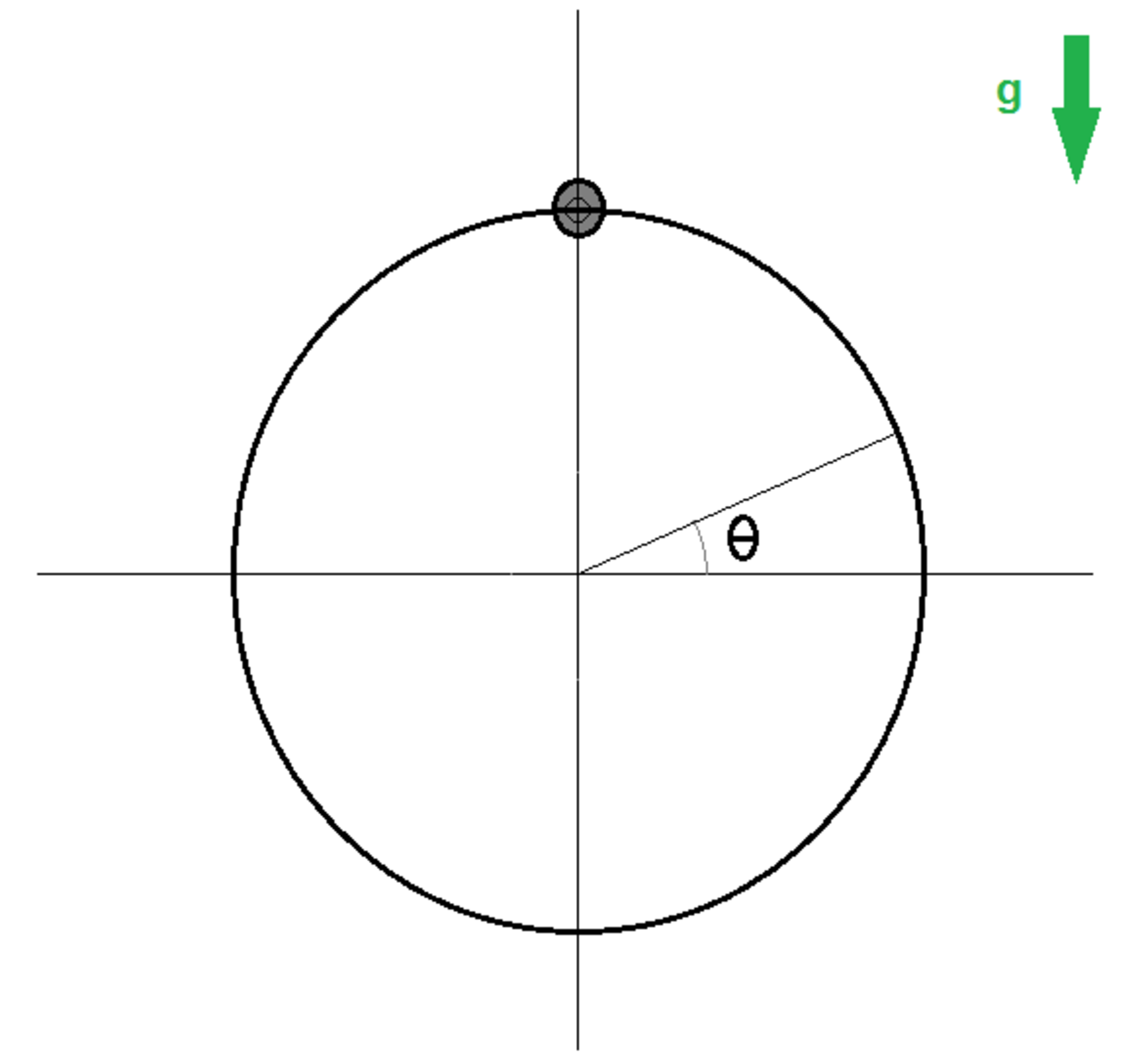
The answer is 64.57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Okay, so I got the wrong answer to this one.
What I did was this. I divided the ring into small arc length elements and considered the tension to be varying with θ . Consider one such element at an angle θ to the horizontal.
I am refraining from drawing a diagram, but by carrying out a force balance in the tangential direction, I obtained:
d θ d T = 2 π M g cos θ
I solved the above and couldn't figure out the rest from there. Here M is the mass of the ring and the other symbols have usual meanings. I am failing to see my mistake here.
Log in to reply
Ok, let my try the infinitesimal approach and see what I get that way. The infinitesimal approach should work too.
Log in to reply
Thanks. Even I think it should work. I request you to update the solution with this approach when you attempt it.
Log in to reply
@Karan Chatrath – I have updated with an infinitesimal analysis as well
Log in to reply
@Steven Chase – Thank you!
I did a force balance along the tangential direction by making a few approximations.
Method 1
Find θ such that:
2 T cos θ = 2 π π + 2 θ M g T = M g ⟹ cos θ = 4 π π + 2 θ
Method 2
Another approach considers the force balance for an infinitesimal segment:
T ( θ ) cos ( θ ) − T ( θ − d θ ) cos ( θ − d θ ) = M g 2 π d θ
The process for each loop iteration is:
1) Store the values for T ( θ − d θ ) and θ − d θ
2) Update the value of θ
3) Solve for T ( θ )
The following code gives the solution for Method 2, and the result is the same