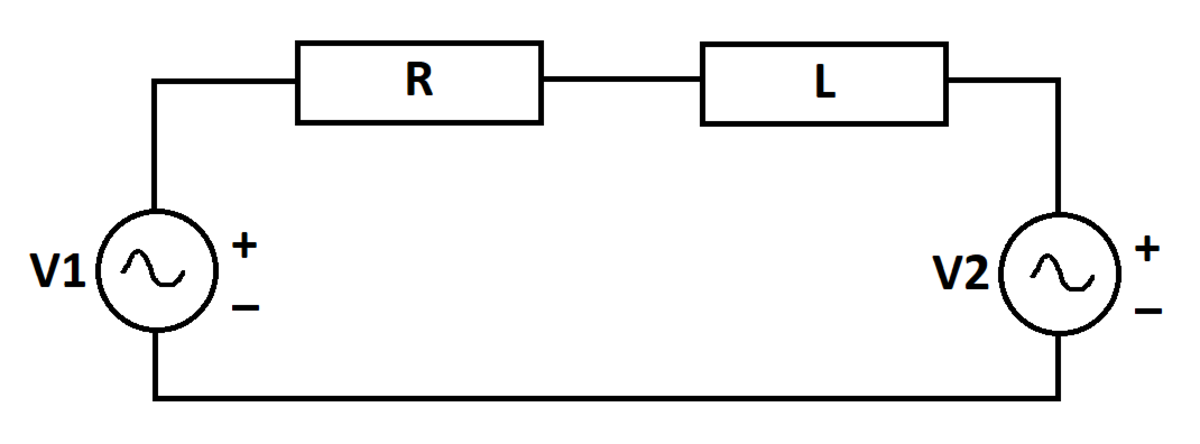
RL Energy Exchange
A resistor and an inductor connect two AC voltage sources, as shown. At time t = 0 , there is no current in the circuit. Let E R ( t ) be the total energy dissipated in the resistor from t = 0 to time t . Let E L ( t ) be the energy stored in the inductor at time t .
What is the largest value of t at which E R ( t ) = E L ( t ) ?
Bonus: Make plots of these two energy quantities over time
Details and Assumptions:
1)
R
=
L
=
1
2)
V
1
(
t
)
=
sin
(
5
t
)
3)
V
2
(
t
)
=
sin
(
3
t
)
The answer is 1.253.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The circuit equation reads:
L I ˙ + R I = V 1 − V 2 ⟹ I ˙ + I = sin ( 5 t ) − sin ( 3 t )
I ( 0 ) = 0
Laplace transform on both sides gives:
I ( s ) = ( s + 1 1 ) ( s 2 + 2 5 5 − s 2 + 9 3 )
Inverse Laplace Transform yields:
I ( t ) = 1 0 3 cos ( 3 t ) − 2 6 5 cos ( 5 t ) − 6 5 7 e − t − 1 0 sin ( 3 t ) + 2 6 sin ( 5 t )
Having found I , we are asked to solve for the largest value of t for which the following holds:
E L = E R ⟹ 2 I ( t ) 2 = ∫ 0 t I ( z ) 2 R d z
Another equally cumbersome route is:
L I ˙ + R I = V 1 − V 2 L I I ˙ + I 2 R = V 1 I − V 2 I L I d I + I 2 R d t = V 1 I d t − V 2 I d t 2 L I 2 + E R = ∫ 0 t V 1 ( z ) I ( z ) d z − ∫ 0 t V 2 ( z ) I ( z ) d z E L + E R = ∫ 0 t ( V 1 ( z ) − V 2 ( z ) ) I ( z ) d z E R = ∫ 0 t ( V 1 ( z ) − V 2 ( z ) ) I ( z ) d z − 2 I ( t ) 2 ⟹ E L + E R = E V 1 − E V 2
The above boxed equation holds true for all instants of time. Plotting E L and E R gives:
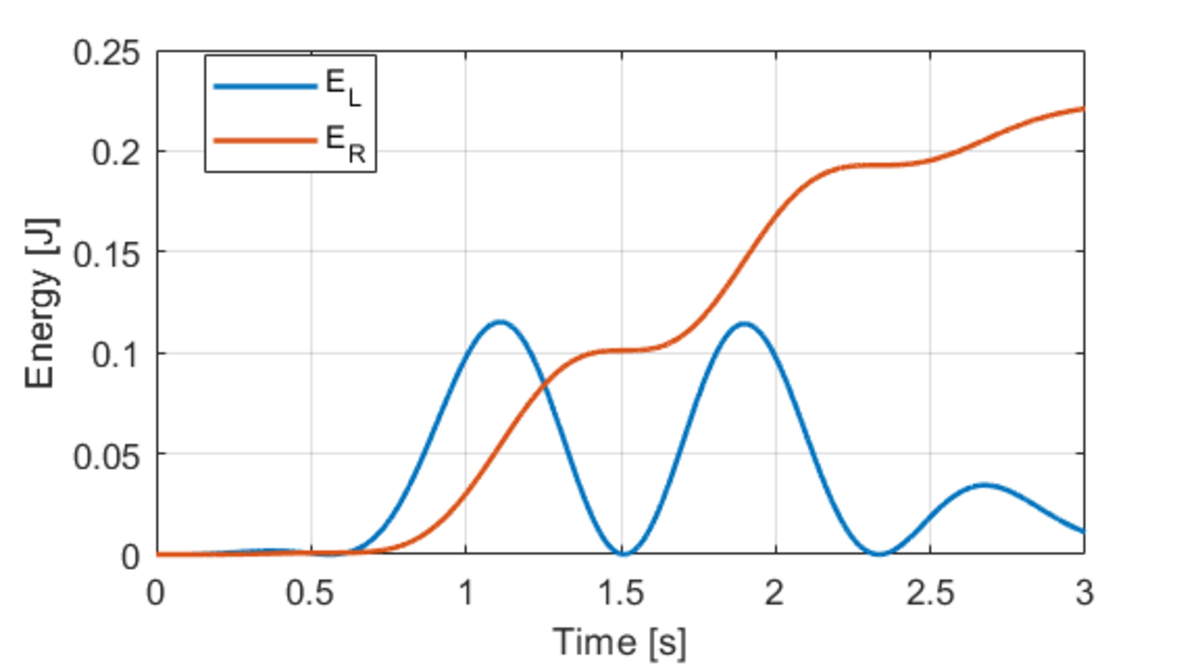
The energy dissipated by the resistor constantly increases as the circuit is supplied with energy from the sources all the time. What makes this problem interesting is doing an energy balance. We know from above that:
E L + E R = E V 1 − E V 2
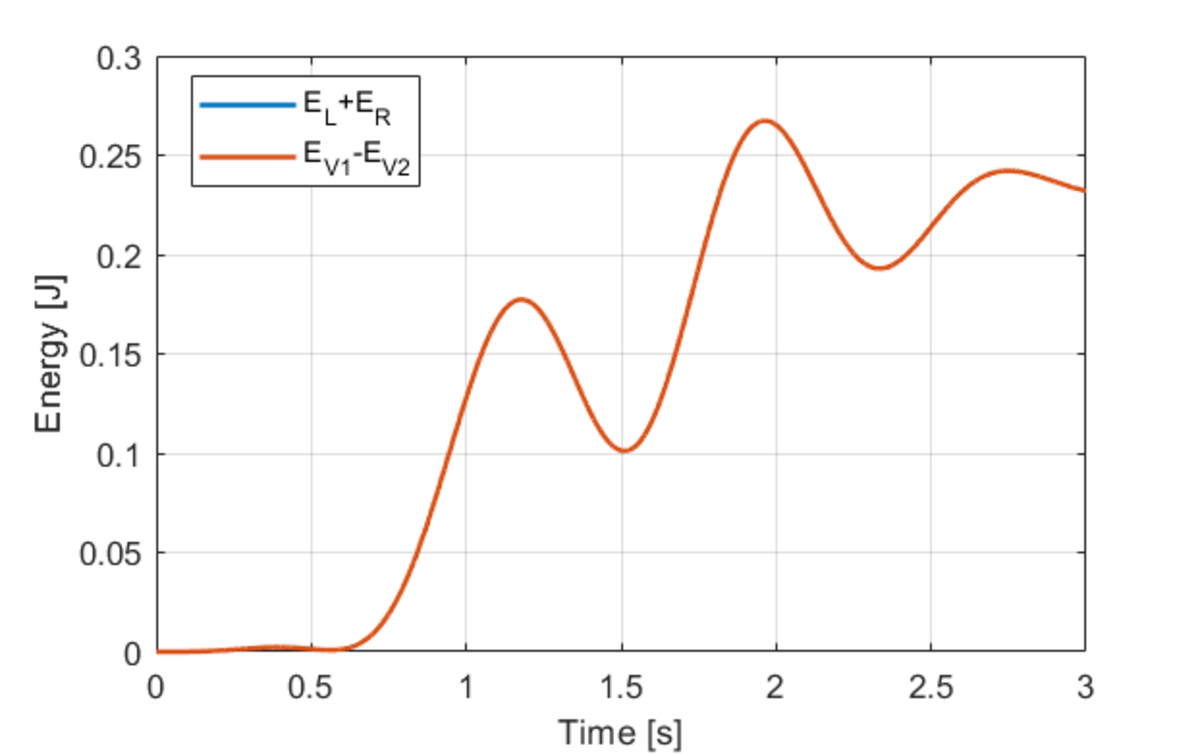
One can see that the two curves perfectly overlap, thus demonstrating the above equation.
Log in to reply
Okay, I did not ask for a solution, but now I am convinced that the problem is badly worded. This is because I misunderstood what α means. Here, α is the coefficient multiplied by time in the exponential term of the solution of the ODE. You are supposed to specify that. So if the solution has the form:
y = e − α t ( … )
The term damping factor or damping ratio can have a completely different meaning. That is usually unity when the response is critically damped. Please work on properly explaining your problems. And in future, do not share solutions here. Instead, clarify as requested.
Log in to reply
If a concept is not so easy to explain in a problem statement, add an additional link to the problems. Do not leave quantities or variables used unexplained or unspecified. These are just some suggestions from my side.
@Karan Chatrath okay.Suggest me whole problem state. Please
Log in to reply
@A Former Brilliant Member – The network shown below has an underdamped response. In other words, in general, any of the states of the system (charge on the capacitors, the current through various elements, etc.) vary with time in the following manner.
x = A e − t sin ( ω t + ϕ )
Here, A , ω and ϕ are constants. Here x is a state variable. Find the value of C which yields such a circuit solution.

F u n P r o b l e m
As @Karan Chatrath sir has provided a very nice solution through Laplace transformation ,I have solved it analytically.
The basic equation is, q is the charge through circuit V 1 − q ˙ − q ¨ − V 2 = 0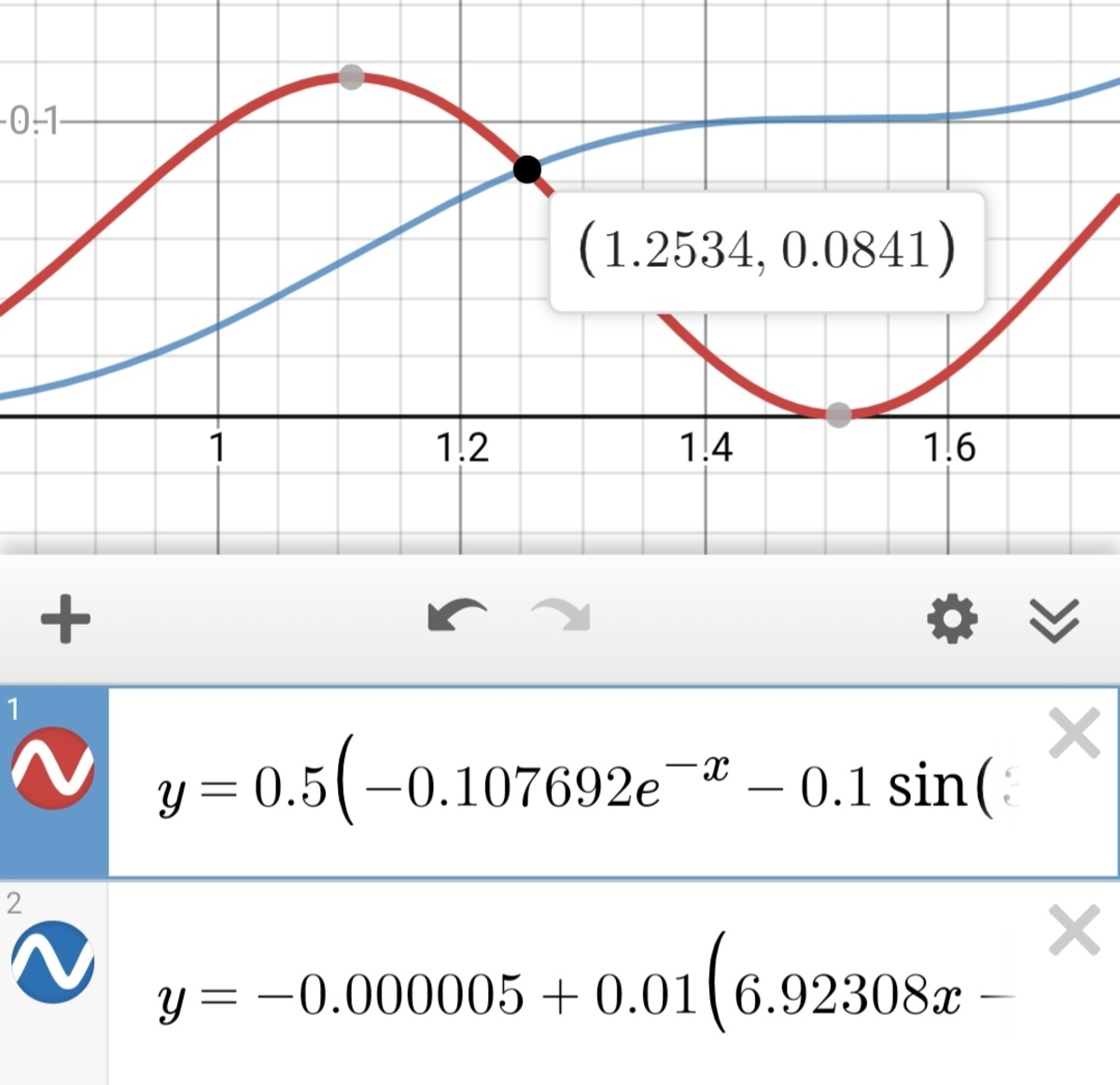
On substituting values s i n ( 5 t ) − q ˙ − q ¨ − s i n ( 3 t ) = 0
On solving the above differential equation q ( t ) = c 1 e − t + c 2 + 0 . 1 s i n ( 3 t ) − 2 6 1 s i n ( 5 t ) + 3 0 1 c o s ( 3 t ) − 1 3 0 1 c o s ( 5 t )
Where c 1 , c 2 are arbitrary constants.
Using the initial conditions q ( 0 ) = 0 q ˙ ( 0 ) = 0 we can easily calculate c 1 and c 2
I get c 1 = + 0 . 1 0 7 6 9 2 c 2 = − 0 . 1 3 3 3 3
Use this value to find the correct differential equation of q ( t )
Differentiate that expression of q ( t ) to get I ( t )
Now to calculate heat dissipated in resistor, use this E r e s i s t o r = ∫ 0 t I 2 ( t ) R d t
Now, the energy stored in inductor E i n d u c t o r = 2 1 L I 2 ( t )
After this I have plotted the graph, as shown below
The 1 s t graph is of inductor. ( y axis denotes to E (energy) and x axis denotes to t (time) )
The largest value of t at which E R ( t ) = E L ( t )
t = 1 . 2 5 3 4
I will also elaborate my solution, if anyone ask.