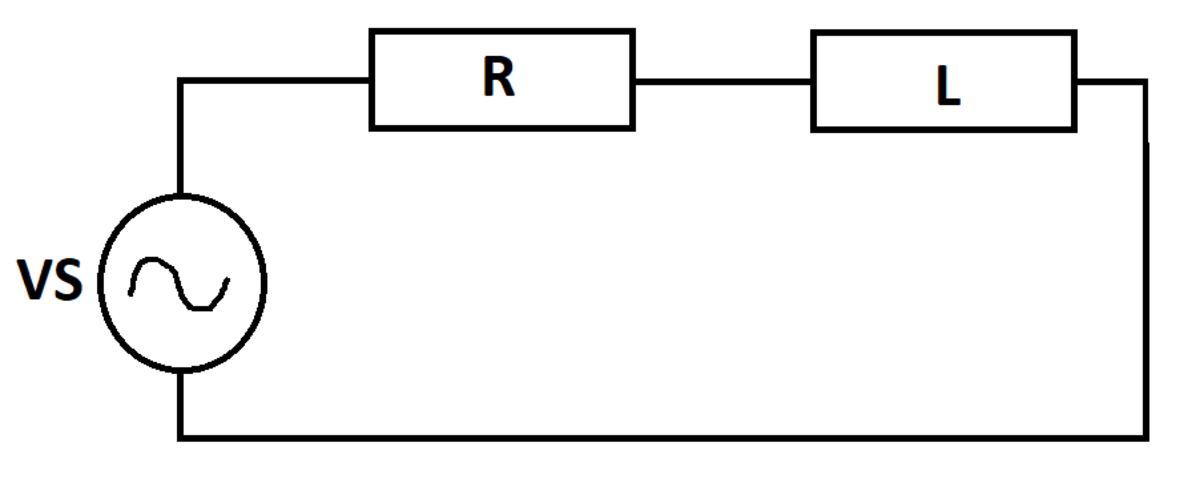
RL with AC Source

$\textcolor{#20A900}{Fun Problem}$
I will be happy if you post more problems like this

I would like to say thanks to Steven sir ,he has helped me so much in python programming.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

import math

L=1
R=1

dt = 10.0**(-7.0)


t = 0.0

I = 0.0
H  = 0

while t <= 0.60*math.pi:

 # Source voltage:
  VS  = 10*math.sin(10*t)

 # Applying Kirchoff's voltage law to get dI/dt
  dI = (VS - I*R)/L

 # Numerical integration:
  I = I + dI*dt

 # Heat dissipation calculation:
  H = H + (I**2)*R*dt

  t = t + dt

print(H)

#1e-05
#1.4120092906323563
#>>>

#1e-06
#1.4119958933725991
#>>>

#1e-07
#1.4119945537214362
#>>> "  

WE are asked to solve the differential equation:

$L\frac{dI}{dt} + IR = 10\sin(10t)$ $I(0)=0$

$\implies \frac{dI}{dt} + I = 10\sin(10t)$ Multiplying both sides by $\mathrm{e}^t$ :

$\implies \mathrm{e}^t\frac{dI}{dt} + \mathrm{e}^tI = 10\mathrm{e}^t\sin(10t)$ $\implies \frac{d}{dt}\left(\mathrm{e}^tI\right) = 10\mathrm{e}^t\sin(10t)$ $\implies d\left(\mathrm{e}^tI\right)=10\mathrm{e}^t\sin(10t) \ dt$

Integrating and applying initial conditions gives:

$I = \frac{10}{101}\left(\sin(10t) - 10\cos(10t)\right) + \frac{100}{101} \mathrm{e}^{-t}$

The heat dissipated in the resistor is:

$\boxed{H = \int_{0}^{3 \pi/5} I^2R \ dt = \int_{0}^{3\pi/5} \left(\frac{10}{101}\left(\sin(10t) - 10\cos(10t)\right) + \frac{100}{101} \mathrm{e}^{-t}\right)^2 \ dt \approx 1.41199}$