RLC 8-1-2020
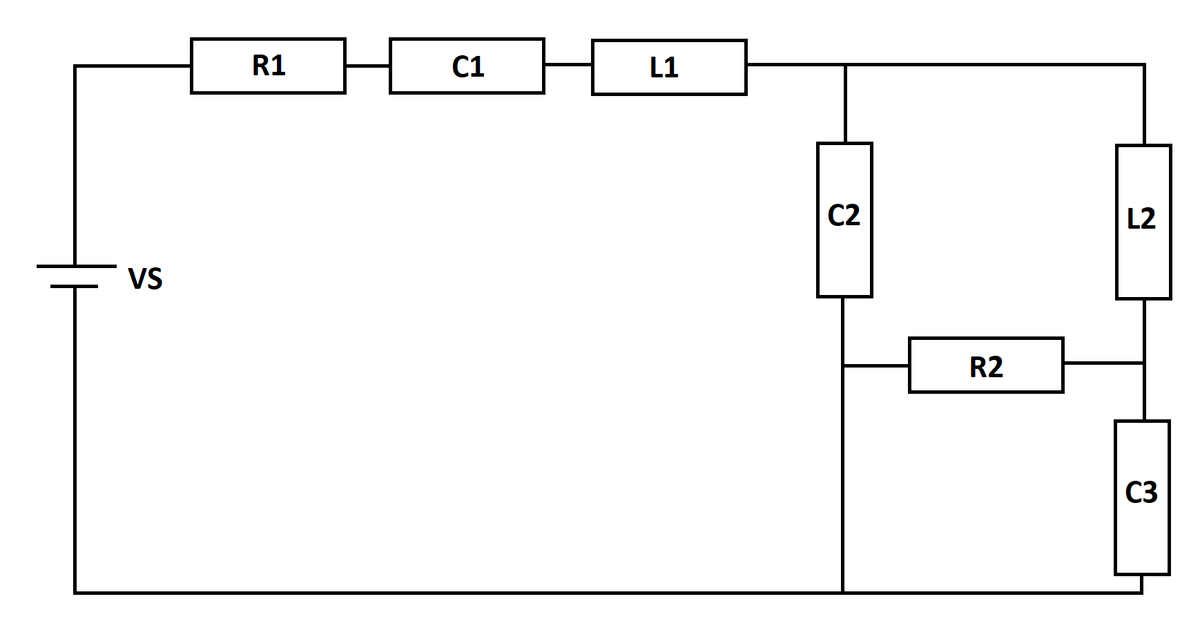
An RLC circuit is excited by a DC voltage source. At time t = 0 , the inductors and capacitors are de-energized. Let P M O be the maximum instantaneous power that ever flows out of the source, and let P M I be the maximum instantaneous power that ever flows into the source.
What is P M I P M O ? Give your answer as a positive number.
Details and Assumptions:
1)
V
S
=
1
0
2)
R
1
=
R
2
=
L
1
=
L
2
=
C
1
=
C
2
=
C
3
=
1
The answer is 8.68.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath please check last 2 hour notifications.
@Karan Chatrath
share your python code .
Thanks in advance.
Log in to reply
Please show your attempt.
Log in to reply
@Karan Chatrath
did you edited it
It was written perhaps??
Log in to reply
@Talulah Riley – No, I did not edit it. I did not share the code in my solution.
I S is the source current and I B is the current through the element-less branch of the 'wheat-stone bridge'. Circuit equations:
I S = I C 2 + I L 2 I C 3 = I R 2 + I L 2 I C 2 = I R 2 + I B
I S = Q ˙ S I C 2 = Q ˙ 2 I C 3 = Q ˙ 3
− V S + R 1 I S + C 1 Q S + L 1 I ˙ S + C 2 Q 2 = 0 L 2 I ˙ L 2 = C 2 Q 2 + R 2 I R 2 R 2 I R 2 + C 3 Q 3 = 0
Numerical integration does the rest. Leaving out those details.
The instantaneous power supplied by the source is: