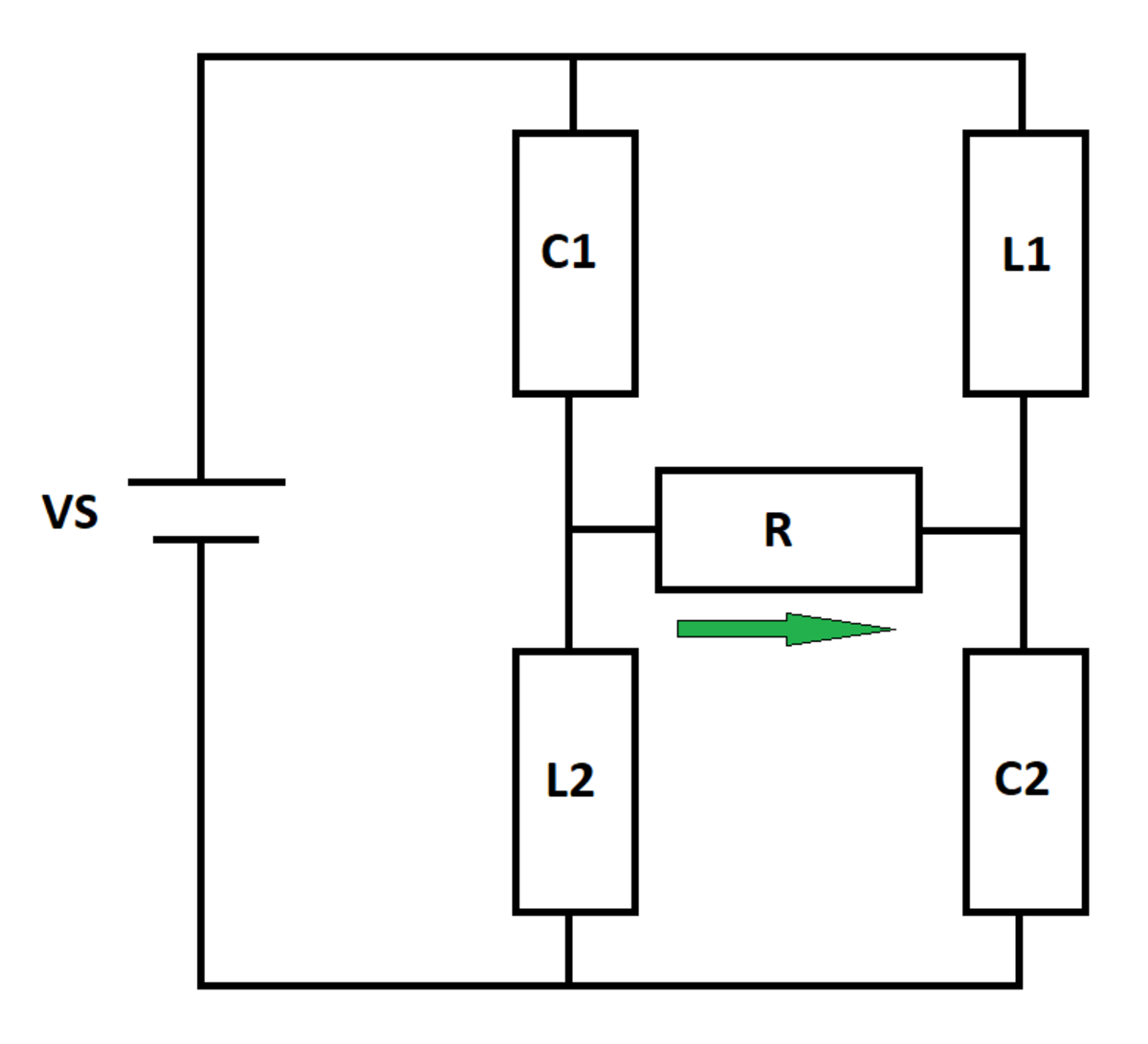
RLC Bridge Circuit

I have done this problem analytically. First, I shall introduce some notation that I have used.

• Current through inductor L1 - $I_2$
• Current through capacitor C1 - $I_1$
• Charge on capacitor C1 - $Q_1$
• Current through resistor (left to right) - $I_o$
• Source current - $I$
• Current through inductor L2 - $I_4$
• Current through capacitor C2 - $I_3$
• Charge on capacitor C2 - $Q_3$

Now, forming equations of the circuit as per Kirchoff's laws gives:

$\dot{Q}_1 = I_1$ $\dot{Q}_3 = I_3$ $I = I_1 + I_2$ $I_3 = I_o + I_2$ $I_1 = I_o + I_4$ $\dot{I}_2 = \frac{Q_1}{5} + I_o$ $\dot{I}_4 = \frac{Q_3}{5} + I_o$ $\frac{Q_1}{5} + \dot{I}_4 = 10$

Taking Laplace transform on both sides of each equation gives:

$sQ_1(s) = I_1(s)$ $sQ_3(s) = I_3(s)$ $I(s) = I_1(s) + I_2(s)$ $I_3(s) = I_o(s) + I_2(s)$ $I_1(s) = I_o(s) + I_4(s)$ $sI_2(s) = \frac{Q_1(s)}{5} + I_o(s)$ $sI_4(s)= \frac{Q_3(s)}{5} + I_o(s)$ $\frac{Q_1(s)}{5} + sI_4(s) = \frac{10}{s}$

Solving for $I_o(s)$ gives the following. The simplification is tedious and this exercise will show why the author of the problem and I both prefer a numerical approach.

$I_o(s) = \frac{10\,\left(5\,s^2-1\right)}{s\,\left(5\,s^2+2\,s+1\right)}$

The resistor current can be computed now by taking the above equation's inverse Laplace transform. This has been done using an online tool, the result of which was simplified further. The result is:

$I_o(t) = \boxed{I_R = 20\,\cos\left(\frac{2\,t}{5}\right)\,{\mathrm{e}}^{-\frac{t}{5}}-10}$

This method, in principle, can be applied to all circuit problems. But be warned that it requires patience and the inverse Laplace transform will not be an easy computation especially when the numerator and denominator polynomials cannot be easily factored.