RLC with Exponential Source

Electricity and Magnetism Level 3

An exponentially decaying voltage source supplies a series R L C RLC circuit as shown. The inductor and capacitor are de-energized at time t = 0 t = 0 . How much energy is dissipated in the resistor from t = 0 t = 0 to t = ∞ t = \infty ?

Details and Assumptions:

  • V S = 10 e − t V_S = 10 e^{-t}
  • R = L = C = 1 R = L = C = 1


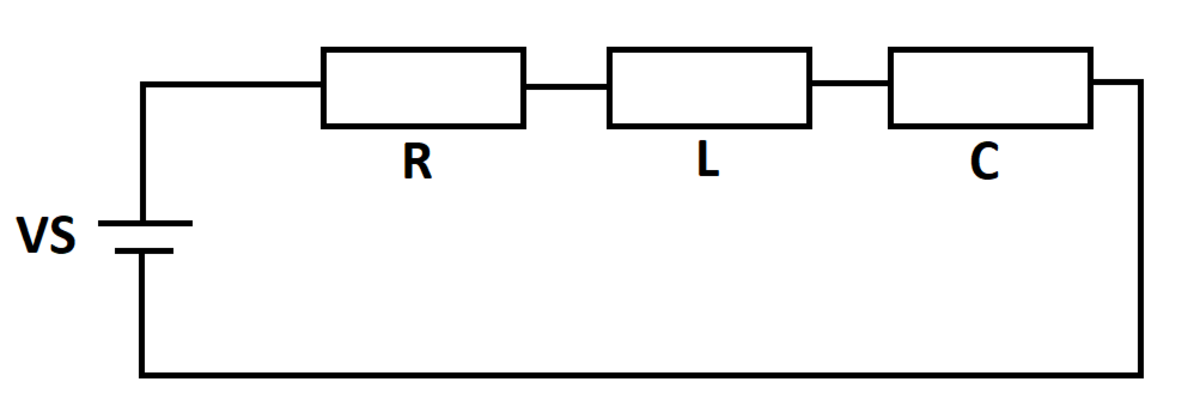
The answer is 16.67.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Talulah Riley
Oct 12, 2020

Basically we are said to solve the double differential equation with initial conditions.

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase I am solving this types of problem from my early childhood. :))

Talulah Riley - 8 months ago

Hey there, your differential equation in the first line, 10 e − t − a ⋅ − a ⋅ ⋅ − a = 0 10 e^{-t} - \stackrel{\cdot}{a} - \stackrel{\cdot\cdot}{a} - a = 0 is not easy to solve. It feels like a cheat that you just asked WolframAlpha for the answer without doing the real work.

Pi Han Goh - 8 months ago

Log in to reply

@Pi Han Goh i used Laplace Transformation with my own in pen and paper. No use of any software.

Talulah Riley - 8 months ago

Log in to reply

Clearly, this solution is far from perfect.

Pi Han Goh - 8 months ago

Log in to reply

@Pi Han Goh – By the way Neeraj, I don't know what you've said after you've deleted your comments. I'm not mad at you or anything. I'm just slightly teasing you by saying that your solution is far from perfect.

Pi Han Goh - 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...