Inequality Masterpiece
( a + b ) 2 a b + 1 + ( b + c ) 2 b c + 1 + ( c + a ) 2 c a + 1
Positive real numbers a , b and c are such that a 2 + b 2 + c 2 + ( a + b + c ) 2 ≤ 4 . Find the minimum value of the expression above.
Question from USAMO 2011 (slightly modified).
Bonus: Prove it and post your solution.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
wow amazing

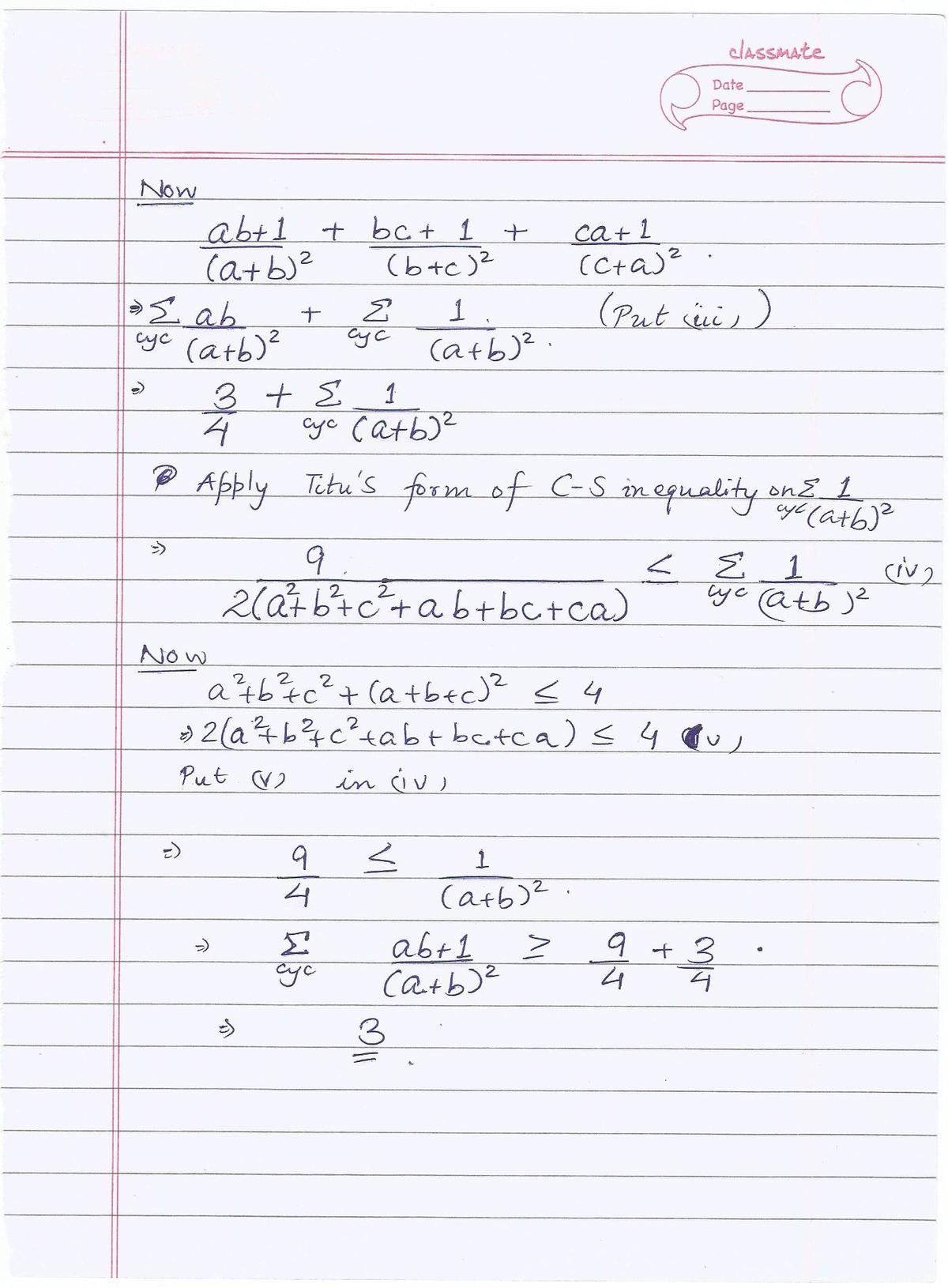 Also the proofs of the inequality used are given below:
https://brilliant.org/wiki/nesbitts-inequality/
Also the proofs of the inequality used are given below:
https://brilliant.org/wiki/nesbitts-inequality/
Proof for the inequality used at the starting of the problem:

@Ashutosh Kumar Nice one !
That was great @Ashutosh Kumar ..!! But could you please elaborate a bit more on the proof of the starting inequality , I couldn't follow that proof.
Log in to reply
The proof of this inequality is quite tough and it was the most simple one but you can find more solution on the internet by searching IRAN 1996 inequality.
Log in to reply
That seems to be extremely tough... AIIT Ashutosh ...Mast inequality padha hai..!
Log in to reply
@Ankit Kumar Jain – haan haan!!!! Tum toh aaj kal aisa aisa banata hai humse banta hi nhi hai
Log in to reply
@Ashutosh Kumar – Hum bana hi nahi rahe hai..mera streak dekh 0 hai.
Log in to reply
@Ankit Kumar Jain – jaa n jaa!!!
We have a 2 + b 2 + c 2 + ( a + b + c ) 2 ≤ 4 ⇔ 2 ≥ a 2 + b 2 + c 2 + a b + b c + c a (1)
We set P = ( a + b ) 2 a b + 1 + ( b + c ) 2 b c + 1 + ( c + a ) 2 c a + 1 ⇔ 2 P = ( a + b ) 2 2 a b + 2 + ( b + c ) 2 2 b c + 2 + ( c + a ) 2 2 c a + 2 (2)
From (1) and (2) we have 2 P ≥ ( a + b ) 2 2 a b + ( a 2 + b 2 + c 2 + a b + b c + c a ) + ( b + c ) 2 2 b c + ( a 2 + b 2 + c 2 + a b + b c + c a ) + ( c + a ) 2 2 c a + ( a 2 + b 2 + c 2 + a b + b c + c a ) ⇔ 2 P ≥ 3 + ( a + b ) 2 ( b + c ) ( c + a ) + ( b + c ) 2 ( c + a ) ( a + b ) + ( c + a ) 2 ( a + b ) ( b + c ) ≥ 3 + 3 = 6 ( A M − G M ) ⇔ 2 P ≥ 6
⇔ P ≥ 3 .