RMO Practice Problem - Algebra 2
Let ( a , b ) be the pair of integers such that
a x 1 7 + b x 1 6 + 1
is divisible by x 2 − x − 1 .
Then find the sum of all such pairs.
Details and Assumptions:
- If you get ( 2 , 3 ) and ( 3 , 4 ) as your answer, then express your answer as sum of all those values i.e. 2 + 3 + 3 + 4 = 1 2 .
Try this set RMO Practice Problems
The answer is -610.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
what a genius . give me some of ur knowledge
Log in to reply
You can shorten the solution even further by noticing: A root of x^2-x-1 must also be a root of ax^17+ bx^16 + 1
As there are two roots you get: a ∗ ϕ 1 7 + b ∗ ϕ 1 6 + 1 = 0 and a ∗ ( 1 − ϕ ) 1 7 + b ∗ ( 1 − ϕ ) 1 6 + 1 = 0
Subtract them from another, divide by 5 , reorder the terms and you can immediately see a and -b are Fibonacci numbers, in fact the 16th and 17th.
I really like the problem, cause there are several short and interesting solutions.
An absolutely genius way to solve.. Too good !! :D
Plus, there is no rocket science involved, 8th grade mathematics ....
hhow u know that only that one pair exists
When f ( x ) = a x 1 7 + b x 1 6 + 1 is divisible by g ( x ) = x 2 − x − 1 . It means that f ( x ) has the same roots as g ( x ) . Now, let us look at x .
\(\begin{array} {} x = x + 0 & \Rightarrow x^1 = \color{blue}{F_1}x + \color{blue}{F_0} \quad \quad \color{blue}{F_n \text{ is the } n^{th} \text{ Fibonacci number}} \\ x^2 = x + 1 & \Rightarrow x^2 = F_2x + F_1 \\ x^3 = x^2 + x = 2x+1 & \Rightarrow x^3 = F_3x+F_2 \\ x^4 = 2x^2+x = 3x + 2 & \Rightarrow x^4 = F_4x+F_3 \\ x^5 = 3x^2 + 2x = 5x + 3 & \Rightarrow x^5 = F_5x+F_4 \\ ... & \Rightarrow x^{16} = F_{16}x + F_{15} \\ ... & \Rightarrow x^{17} = F_{17}x + F_{16} \end{array} \)
⇒ a x 1 7 + b x 1 6 + 1 ( a F 1 7 + b F 1 6 ) x + a F 1 6 + b F 1 5 + 1 = 0 = 0
Equating the coefficients on both sides, we have:
{ a F 1 7 + b F 1 6 = 0 a F 1 6 + b F 1 5 = − 1 . . . ( 1 ) . . . ( 2 )
{ ( 1 ) × F 1 5 : ( 2 ) × F 1 6 : a F 1 5 F 1 7 + b F 1 5 F 1 6 = 0 a F 1 6 2 + b F 1 5 F 1 6 = − F 1 6 . . . ( 3 ) . . . ( 4 )
{ ( 3 ) − ( 4 ) : ( 1 ) : ( F 1 5 F 1 7 − F 1 6 2 ) a = F 1 6 F 1 6 F 1 7 + b F 1 6 = 0 ⇒ ( 1 ) a = F 1 6 ⇒ b = − F 1 7 By Cassini’s identity*
⇒ a = F 1 6 and b = − F 1 7 and a + b = F 1 6 − F 1 7 = − F 1 5 = − 6 1 0
∗ Cassini's identity F n − 1 F n + 1 − F n 2 = ( − 1 ) n
This solution is not true. The equation a F 1 6 + b F 1 5 = − 1 does not have single integer solution. For instance, (a,b) = ( F 1 4 , − F 1 5 ) holds true (and this one looks like your "Cassini's solution"). More generally, a pair with this form ( F 1 6 − k F 1 5 , − F 1 7 + k F 1 6 ) is a solution with k is an arbitrary integer. The last two "if/then" statements are wrong.
Log in to reply
I actually worked it out numerically first.
a x 1 7 + b x 1 6 + 1 ( a F 1 7 + b F 1 6 ) x + a F 1 6 + b F 1 5 + 1 = 0 = 0 .
Equating the coefficients on both sides, we have:
{ a F 1 7 + b F 1 6 = 1 5 9 7 a + 9 8 7 b = 0 a F 1 6 + b F 1 5 = 9 8 7 a + 6 1 0 b = − 1 . . . ( 1 ) . . . ( 2 )
{ ( 1 ) × 6 1 0 : ( 2 ) × 9 8 7 : 9 7 4 1 7 0 a + 6 0 2 0 7 0 b = 0 9 7 4 1 6 9 a + 6 0 2 0 7 0 b = − 9 8 7 . . . ( 3 ) . . . ( 4 )
{ ( 3 ) − ( 4 ) : ( 1 ) : ( 1 ) a = 9 8 7 = F 1 6 Note that F 1 5 F 1 7 − F 1 6 2 = 1 1 5 9 7 ( 9 8 7 ) + 9 8 7 b = 0 ⇒ b = − 1 5 9 7 = − F 1 7
a + b = F 1 6 − F 1 7 = − F 1 5 = − 6 1 0
I have done at least two other similar problems before without knowing Cassini's. I have consistently got the same results and found it beautiful.
Log in to reply
I agree with you that your idea is beautiful and comes naturally. But if you use the Cassini's as your "shortcut" like that, it may cause problems. Let's work on the system of (1) and (2). Since g cd ( F n + 1 , F n ) = 1 , solutions of (1) take form (a,b) = ( F 1 6 k , − F 1 7 k ) . Let it take place of (a,b) in (2), by the identity we get the unique k = 1 immediately. I think that's how Cassini's used in your solution. We can't get the answer to the original problem if we just only solve (2). That's what I mean.
Log in to reply
@Trongnhan Khong – Yes, you are right. I have changed the solution.
Let p , q be the roots of the equation x 2 − x − 1 . By Vieta's theorem p + q = 1 and p q = − 1 . Note that p and q must also be the roots of a x 1 7 + b x 1 6 + 1 = 0 . Thus
a p 1 7 + b p 1 6 = − 1 and a q 1 7 + b q 1 6 = − 1 .
Multiplying the first of these equations by q 1 6 , the second one by p 1 6 , and using the fact that p q = − 1 , we find
a p + b = − q 1 6 and a q + b = − p 1 6 . ( 1 )
Thus
a = p − q p 1 6 − q 1 6 = ( p 8 + q 8 ) ( p 4 + q 4 ) ( p 2 + q 2 ) ( p + q ) .
Since
p + q = 1 ,
p 2 + q 2 = ( p + q ) 2 − 2 p q = 1 + 2 = 3
p 4 + q 4 = ( p 2 + q 2 ) 2 − 2 ( p q ) 2 = 9 − 2 = 7
p 8 + q 8 = ( p 4 + q 4 ) 2 − 2 ( p q ) 4 = 4 9 − 2 = 4 7
it follows that a = 1 . 3 . 7 . 4 7 = 9 8 7 .
Likewise, eliminating a in ( 1 ) gives
− b = p − q p 1 7 − q 1 7
= ( p 1 6 + q 1 6 ) − ( p 1 4 + q 1 4 ) + . . . − ( p 2 + q 2 ) + 1
For n > 1 , let k 2 n = p 2 n + q 2 n . Then k 2 = 3 and k 4 = 7 , and
k 2 n + 4 = p 2 n + 4 q 2 n + 4
= ( p 2 n + 2 + q 2 n + 2 ) ( p 2 + q 2 ) − p 2 q 2 ( p 2 n + q 2 n
= 3 k 2 n + 2 − k 2 n
for n ≥ 3 . Then k 6 = 1 8 , k 8 = 4 7 , k 1 0 = 1 2 3 , k 1 2 = 3 2 2 , k 1 4 = 8 4 3 , k 1 6 = 2 2 0 7 .
Hence,
− b = 2 2 0 7 − 8 4 3 + 3 2 2 − 1 2 3 + 4 7 − 1 8 + 7 − 3 + 1 = 1 5 9 7
or
( a , b ) = ( 9 8 7 , − 1 5 9 7 ) .
So, a + b = 9 8 7 − 1 5 9 7 = − 6 1 0 .
Thus, answer : − 6 1 0 .
why did you equated the co-efficient of x and constant term equal to ZERO?
In what follows we are going to assume that x 2 − x − 1 divides a x 1 7 + b x 1 6 + 1 . Then we can see that any solution of x 2 − x − 1 = 0 must be a solution of a x 1 7 + b x 1 6 + 1 = 0 .
Let
α
represent a solution of
x
2
−
x
−
1
=
0
,
then
α
2
=
α
+
1
,
and therefore for any natural number
n
we have that
α
n
+
2
=
α
n
+
1
+
α
n
.
(
1
)
Now we can prove using induction that for any pair of real numbers
c
and
d
and for any natural numbers
n
>
2
and
k
<
n
the following is true:
c
α
n
+
d
α
n
−
1
=
(
F
k
+
1
c
+
F
k
d
)
α
n
−
k
+
(
F
k
c
+
F
k
−
1
d
)
α
n
−
k
−
1
(
2
)
where
F
m
represents the
m
−
term of the Fibonacci sequence defined by
F
0
=
0
,
F
1
=
1
and
F
m
+
1
=
F
m
+
F
m
−
1
.
Let us prove first that (2) is true for
k
=
1
. Indeed, using (1) we get that
c
α
n
+
d
α
n
−
1
=
c
(
α
n
−
1
+
α
n
−
2
)
+
d
α
n
−
1
=
(
c
+
d
)
α
n
−
1
+
c
α
n
−
2
=
(
F
2
c
+
F
1
d
)
α
n
−
1
+
(
F
1
c
+
F
0
d
)
α
n
−
2
.
Now let us prove that if (2) is true for any number natural
k
<
n
then is would be true also for
k
+
1
, of course, if
k
+
1
<
n
.
Applying
(
1
)
again we get that
c
α
n
+
d
α
n
−
1
=
(
F
k
+
1
c
+
F
k
d
)
α
n
−
k
+
(
F
k
c
+
F
k
−
1
d
)
α
n
−
k
−
1
=
=
(
F
k
+
1
c
+
F
k
d
)
(
α
n
−
k
−
1
+
α
n
−
k
−
2
)
+
(
F
k
c
+
F
k
−
1
d
)
α
n
−
k
−
1
=
(
(
F
k
+
1
+
F
k
)
c
+
(
F
k
+
F
k
−
1
)
d
)
(
α
n
−
k
−
1
)
+
(
F
k
+
1
c
+
F
k
d
)
α
n
−
k
−
2
=
(
F
k
+
2
c
+
F
k
+
1
d
)
α
n
−
k
−
1
+
(
F
k
+
1
c
+
F
k
d
)
α
n
−
k
−
2
.
This completes the proof of (2)
Now using (2) with n = 1 7 and k = 1 5 we obtain that if α is a zero of x 2 − x − 1 = 0 then 0 = a α 1 7 + b α 1 6 + 1 = ( F 1 6 a + F 1 5 b ) α 2 + ( F 1 5 a + F 1 4 b ) α + 1 = = ( 9 8 7 a + 6 1 0 b ) α 2 + ( 6 1 0 a + 3 7 7 b ) α + 1 .
Therefore the polynomial a x 1 7 + b x 1 6 + 1 is divisible by x 2 − x − 1 if and only if ( 9 8 7 a + 6 1 0 b ) x 2 + ( 6 1 0 a + 3 7 7 b ) x + 1 is divisible by x 2 − x − 1 . Then 9 8 7 a + 6 1 0 b = − 1 and 6 1 0 a + 3 7 7 b = − 1 . The only solution of this system of equations is ( a , b ) = ( 9 8 7 , − 1 5 9 7 ) . So the answer to the question is a + b = 9 8 7 − 1 5 9 7 = − 6 1 0 .
For a x 1 7 + b x 1 6 + 1 to be divisible by x 2 − x − 1 , a λ 1 7 + b λ 1 6 + 1 = 0 should be true for λ being the roots of x 2 − x − 1 = 0
We can easily get λ = 2 1 ± 1 + 4 = 2 1 ± 2 5 .
Substituting for λ we have two linear equations in a , b as
( 2 1 + 2 5 ) 1 7 a + ( 2 1 + 2 5 ) 1 6 b = − 1
( 2 1 − 2 5 ) 1 7 a + ( 2 1 − 2 5 ) 1 6 b = − 1
Using Cramer's rule,
a = ( 2 1 + 2 5 ) 1 7 ( 2 1 − 2 5 ) 1 6 − ( 2 1 − 2 5 ) 1 7 ( 2 1 + 2 5 ) 1 6 − ( 2 1 − 2 5 ) 1 6 + ( 2 1 + 2 5 ) 1 6 = 9 8 7
b = ( 2 1 + 2 5 ) 1 7 ( 2 1 − 2 5 ) 1 6 − ( 2 1 − 2 5 ) 1 7 ( 2 1 + 2 5 ) 1 6 ( 2 1 − 2 5 ) 1 7 − ( 2 1 + 2 5 ) 1 7 = − 1 5 9 7
Thus, giving a + b = − 6 1 0
I have done exactly the way you did. There is only one pair namely (987, -1597).
This is not a solution.
Use long division and you will find that remainder in each step follows a pattern. Find the pattern and find remainder finally. If the final remainder is mx+n, then m=n=0. Using this, try to get the values of a and b.
Elaborating:- m = F ( 1 7 ) × a + F ( 1 6 ) × b
n = F ( 1 6 ) × a + F ( 1 5 ) × b + 1
Solve m = n = 0 as stated to get a and b
F ( n ) is the nth Fibonacci term.
sir can you please show that how a pattern is followed
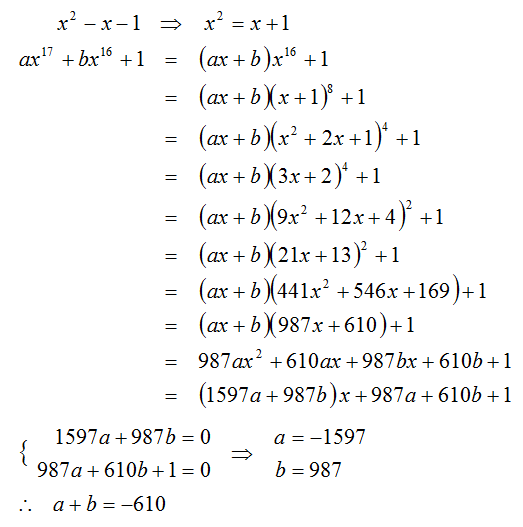
We are looking for a , b such that a x 1 7 + b x 1 6 = x 1 6 ( a x + b ) = − 1 , where
x 2 = x + 1 ⟹ x 4 = x 2 + 2 x + 1 = 3 x + 2 ⟹ x 8 = 9 x 2 + 1 2 x + 4 = 2 1 x + 1 3
⟹ x 1 6 = 4 4 1 x 2 + 5 4 6 x + 1 6 9 = 9 8 7 x + 6 1 0 .
Now x 2 − x − 1 = 0 ⟹ x = 2 1 ± 5 , so x 1 6 = 9 8 7 ∗ 2 ( 1 ± 5 ) + 6 1 0 = 2 2 2 0 7 ± 9 8 7 5 .
Thus a x + b = − x 1 6 1 ⟹ a ∗ 2 ( 1 ± 5 ) + b = − 2 2 0 7 ± 9 8 7 5 2
⟹ ( a + 2 b ) ± a 5 = − 2 2 0 7 ± 9 8 7 5 4 ∗ 2 2 0 7 ∓ 9 8 7 5 2 2 0 7 ∓ 9 8 7 5 = − 2 2 0 7 ± 9 8 7 5 .
So for both cases we have that a = 9 8 7 and a + 2 b = − 2 2 0 7 ⟹ b = − 1 5 9 7 , and so
a + b = 9 8 7 + ( − 1 5 9 7 ) = − 6 1 0 .