Roboant

Instead of imagining the roboants colliding each other, imagine them passing through each other. We can do this because the result is the same: two roboants come in facing towards each other, and they leave facing away from each other.

This version of the problem is much simpler. Each of the $30$ roboants pass by the $20$ roboants on the other side, for a total of $30 \times 20 = \boxed{600}$ collisions.

I think it's a good idea to solve the problem recursively. The total number of bumps is the number of bumps of the left group plus the bumps of the right group. From each group, the total bumps is the bumps of the outermost ant (1 only) plus the bumps of the inner group. Always keeping in mind that you don't have to double count bumps.

First, I count the bumps of the right group (20 ants). I start from the rightmost ant. The 20th one bumps 1 time with the 19th. The 19th bumps 1 times with the 20th (but that's counted already) and 2 times with the 18th: so it's 2 bumps to add. So on till the 1st one of the right group, that bumps 20 times with the last of the left group. Total number of bumps of the right group is the sum of i from 1 to 20, that is 210.

Then, left group. Starting from the leftmost ant, called 1st. 1st bumps once with 2nd. Then, 1 bump 2nd bumps once with 1st (already counted), twice with the 3rd. Then, 2 more bumps. So on till the 20th, bumping 20 times.

From ant 21th to 30th of the left group, they bump 20 more times each, since the left group goes away after 20 bumps. 21th bumps into 20th 20 times (already counted), then 20 times with 22th, that turns right afterwards. Then 20 more bumps. 22th does 20 more bumps vs 23th. So on till 29th, with 20 more bumps into 30th. 30th bumps with 29th (already counted ) and the 1st of the right group (already counted). So doesn't make new bumps. Total number of bumps of the right group: sum of i from 1 to 20, plus 9 times 20: then it's 210+180 = 390. Total bumps: left group bumps + right group bumps = 600.

Due to a friend: start with one ant crossing 20 ants. They will have 20 collisions. Then add another ant. After analysis: they will have 40 collisions. Omitting the induction proof, the answer is 30*20=600.

Well, in my case, it turned out to be the sum of an arithmetic progression. Just imagine, after the collision, the ant turned around and collided with his fellow ants, coming from his end without turning . Now, for the first pair of ants, no. of collisions =1+19+29=49, and for the second pair of ants, it will be =1+18+28=47. Similarly proceeding, we get an AP: 49, 47, 45, ... with common difference -2. It will have 20 terms. So, we can find the total no. of collisions by finding the sum of this AP, by using the formula, S = n/2(2a+(n-1)d) =10(98-38) =600

We have 20 roboants that are about to meet 30. As each of the 20 roboants meets 30 roboants. As we have 20 roboants, we have the number of ants that meet one roboant time the number of roboants on the other group. 20 times 30 makes 600.

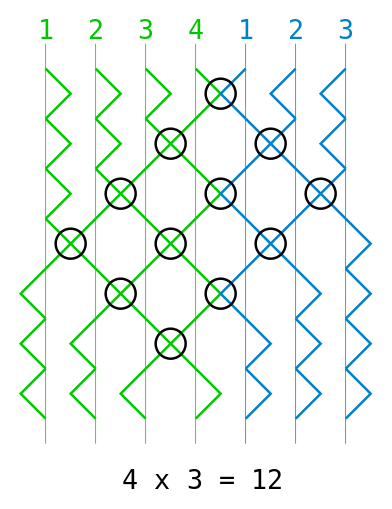
If you draw successive states as a series of rows, it becomes apparent that the collisions form an $m \times n$ rectangle.

A solution without assuming the ants pass each other (even though that one is "better" (faster)): $m=30, n=20; m>n$

First iteration: Two ants make one collision, call them left $_1$ and right $_1$

Second iteration: The two ants collide with other two ants, call them left $_2$ and right $_2$

Third iteration: Left $_2$ collides with nother ant, left $_3$ , and right $_2$ with some other ant, right $_3$ ; while left $_1$ and right $_1$ collide with each other again. In total 3 collisions in this iteration.

Generalizing, there will be $\frac{n(n+1)}{2}$ collisions up to iteration $n$ . That is to say, there are $k$ collisions for iteration $k$ . But, after that, in iteration $n+1$ there will be only $n$ collisions again, since the collision that should be added, is lost by an ant that goes out the tube since she doesn't have another ant to collide into..

This will continue up to iteration $m$ . Let's consider though, only up to iteration $m-1$ , since iterations $m$ and onward are a mirror of iterations $1$ to $n$ .

So in iterations $1$ to $n$ , we have $\frac{n(n+1)}{2}$ . In iterations $m$ to $m+n$ we have $\sum_{i=m}^{m+n-1}i=\frac{n(n+1)}{2}$ . And in iterations $n$ to $m-1$ we have $n$ times $m-(n+1)$ .

That is to say, summing all: $2 \frac{n(n+1)}{2} + n(m-n-1) = n(n+1+m-n-1)=nm$ .

If $n=20$ and $m=30: nm=\boxed{600}$ .

Imagine an x-t diagram, where t runs vertically downward. 30 lines from NW to SE cross 20 lines from NE to SW. Each cross point is a collision where two ants meet and change direction. You could track them individually, but there's no need to do that to get the answer: 600 cross points.

Let us imagine there are only 2 ant on either side,then the number of collsions is 1.Now if there is 1 ant on one side and 2 on other side then number of collisions are 2.Now if 2 on one and 2 on other side then 4.If 1 and 3 then answer is 3,if 3 and 3 then 9,if 1and 4 then 4.We see that the number of collisions is the product of number of ants on either sides.So the number of collisions here 30*20=600

You need to recognize that the bumping is basically equivalent to one passing through another (as if they were ghosts) for this calculations. After that it is fairly simple, 1 ant in the 20 ant group goes through 30 ants in the other group, and there are 20 ants, so the total number of ants going through is 30*20=600 (remember that the going through is technically a collision). I know this solution is already there but I am also trying to improve my explanation skills and I did use this method.

Imagine there are 3 robot ants on the right side and 2 on the left side arranged as:

R3 R2 R1 L1 L2

•R1 will collide with L1 (collision 1) Causing L1 to change direction & collide with L2 changing directions again. (Collision 2)

•R1 will collide with R2 leading to R2 colliding with R3. (Collision 3,4) Since R3 and L2 have changed directions, they leave the tube.

•this repeats again causing R3 and L2 to leave the tube.(Collision 5,6)

Total collisions = 6 = 2x3 Same way, collisions for 30 ants on the left side and 20 on the right side = 20x30 = 600

Whenever I try to post a thorough solution it gets too long and won't let me post, so I'll have to be brief. For two groups of n and n+m ants the n ants in the smaller group (as well as the outermost n is the larger) have 1,3,5,...,2n-1 collisions. Adding 1 to 2n-1 gives 2n and we can continue to do this n/2 times. The remaining m ants each have 2n collisions. We only want half of these collisions as they count each ants' therefore counting each collision twice. This gives $2n×\frac n2 + 2n×\frac m2$ (we don't count the 2n × n/2 collisions from the larger group). So we get $\frac{2n^2}{2} + \frac{2nm}{2}$ . Simplifying gives $n^2 + nm$ and factorising gives $n(n +m)$ ie the product of the number of ants in the two groups $\boxed{QED}$ .

Let's view this situation in terms of collision stage .

In each stage, the number of collision sites increases by 1 and additional collision sites are created at either side of tube as long as roboants are there . Also the adjacent collision sites turn on alternately as one can observe/verify. This will happen as long as 🐜 are there on either side. After that collision sites will recede at end will lower 🐜 (🐜 start moving one side) but increase at end with higher no. of 🐜, which cumulatively will constantiate no. of collisions. Then, even the end with higher 🐜 will see 🐜 moving one side and collisions will start receding till it reaches to one collision. Based on this reasoning the number of collisions,

N= $S1 + S2 + S3$

S1 = No. of collisions where no 🐜 are moving to ends=

$1 + 2 + 3 + \ldots + 20$

S2 = No. of collisions where 🐜 at side with lower 🐜 only at moving at respective ends

= ( $21 - 1) + (22 - 2) + \ldots + (30 - 10)$

= $20 \times 10$

S3 = No. of collisions where 🐜 at both side move to respective end

= ( $31 - 11 - 1) + (32 - 12 - 2) + \ldots + 1$

Summing the three up, we get,

N = 600.

I tried it out with smaller numbers and found a pattern. If a and b are the numbers of ants on respective sides, with b being the smaller number you will get 1 collision first turn, 2 second turn, 3 third and so on up to a maximum of b collisons. You will get maximum number of collisions for a-b+1 turns and then go down from b to 1 again. This gives a complicated formula of b(b+1)+b(a-b-1)+b(b+1). This can be simplified to ab!! Now I will go on to read other much better solutions. :)

If you draw down the ants as dots, then assume the y-axis as time. Then draw diagonal lines parallel with each side (of ants) under the dots you’ll get the paths of the ants. And wherever the lines meet is a turning point so you’ll find out that the number they meet will be the amount of points the diagonal lines meet, which is 30*20=600