Rod and particle
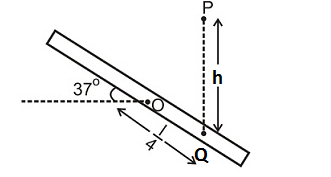
Consider a rod of mass M and length L is free to rotate about an horizontal axis O passing through its center. A particle of mass m falls from point P which is at a height h from Q and collides elastically with rod at a distance 4 L form O . If the rod makes an angle α with horizontal before collision. Then find the angular velocity of rod just after collision.
Details And Assumptions
- The Rod is at rest before collision
- M = 2.5 kg
- L = 4 m
- m = 2 kg
- h = 5 m
- α = 3 7 ∘
- Take g = 1 0 m / s 2
The answer is 5.98.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Problem is nice but shouldn't it be specified to take g as 10 because i took 9.8 initially and got wrong answer
Log in to reply
Sorry for trouble, i have mentioned it
Log in to reply
Thanks ! also i had a strong feeling from inside to take g as 9.8 because in answer box it was written that decimals ok :)
What is the equation of e
Can u explain the physical meaning of the e equation and how u got there
Log in to reply
The equation of e the the equation for coefficient of restitution (e) = velocity of approach of objects velocity of separation of objects
how did you get initial angular momentum = m ∗ 5 4 v
Log in to reply
sorry its just a typo it should be m × 5 4 v × 4 l .
It is because we need to take component of velocity perpendicular to rod to calculate initial angular momentum.
Log in to reply
Great solution, are you in fiitjee south delhi
i first did by a different method but ended with a wrong answer ,
i'll be glad if u tell my mistake ,first i found the velocity of particle in direction perpendicular to the rod let it be v' ,
v be the initial perpendicular velocity of the particle which is ( 2 g h ) cos 3 7 the net impulse on rod is m(v+v')
Now using angular impulse - momentum theorem 1 2 M l 2 angular velocity = m(v+v') l/4
after solving i get 5.3333
can u tell what is wrong in my approach ?
i firstly didn't feel like conserving momentum as impulse is acting at the point of contact and hinge will also apply an impulse.
@Mark Hennings sir
Log in to reply
Look at my comment...
Log in to reply
which comment sir ?
Log in to reply
@A Former Brilliant Member – Sorry, report.
Log in to reply
@Mark Hennings – When you are using impulses, you are conserving angular momentum, presuming that the particle has perpendicular speed v ′ after the collision. This is right. However, you never say how you calculate v ′ , so I don't know how the second half of your argument goes...
Log in to reply
@Mark Hennings – v' is calculated by usual conservative of momentum and elasticity condition .
Just conserve angular momentum and put the condition of elasticity.
Can you please post the full solution.Thanks
Log in to reply
By conservation of energy and angular momentum I am getting ans as 3. Please explain how to use condition of elasticity. Also I am not able to see the correct ans even after clicking on veiw solution. So pl tell the correct ams
Let v 0 be the velocity of particle before collision. And ω the angular velocity of road after collision and v x and v y the component of particle just after collision along and perpendicular the rod respectively
From the equation of e along the line of impact:
e = 1 = − 0 − 5 4 × v 0 4 l × ω − v y
→ 4 l × ω − v y = 5 4 × v 0
Now conserving angular momentum form the point where rod is attached to the axis:
m × 5 4 v 0 × 4 l = m v y × 4 l + I ω , where I is the moment of inertia of rod ( I = 1 2 m l 2 )
Now substituting the value of v y we get ω = 6