Rojo, azul y verde

Geometry Level 2

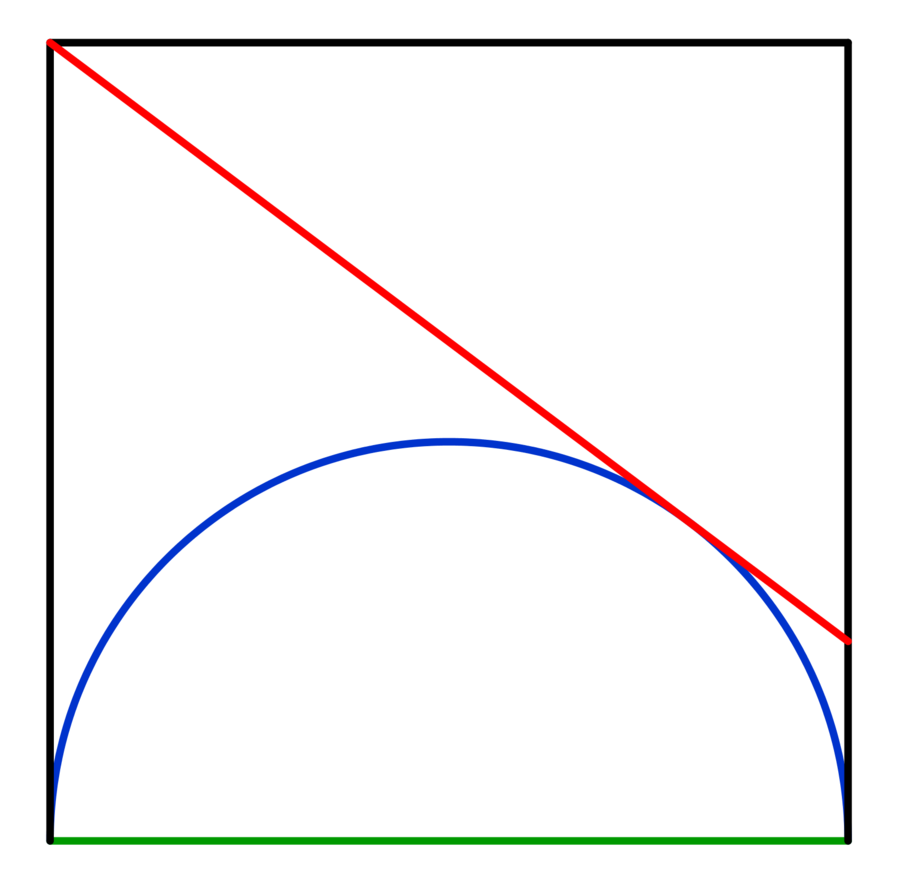
The figure above shows a square with perimeter 32 cm. The diameter of the inscribed blue semicircle is the green side of the square. A red tangent to the blue semicircle is drawn joining the square upper left vertex and a point on its right side. Find the length of the red tangent in cm.

The answer is 10.

4 solutions

Aareyan Manzoor
Jul 21, 2019

we find using the red right triangles that $\sin(\theta)= \dfrac{1}{\sqrt{5}} , \cos(\theta) = \dfrac{2}{\sqrt{5}}$ . the desired lenght using the right triangle with the blue base is $\dfrac{8}{\sin(2\theta)} = \dfrac{8}{2\sin(\theta)\cos(\theta)} = \boxed{10}$

David Vreken
Jul 22, 2019

Let the square be $PQRS$ , let $T$ be the tangent point of the red tangent line and the semicircle, let $U$ be the center of the semicircle, and let $V$ be the intersection of the red tangent line and $QR$ . Let $x = VR$ .

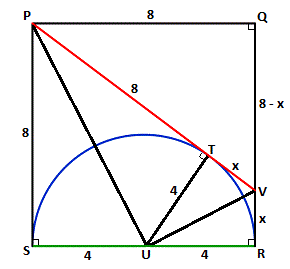
Since the perimeter of the square is $32$ cm, each side is $8$ cm, and the radius of the semicircle is $4$ cm.

$\triangle PSU \cong \triangle PTU$ and $\triangle VRU \cong \triangle VTU$ by HL congruence, therefore $PT = PS = 8$ cm and $TV = VR = x$ .

By Pythagorean's Theorem on $\triangle PQV$ , $8^2 + (8 - x)^2 = (8 + x)^2$ , which solves to $x = 2$ cm.

Therefore, the red tangent line is $8 + x = 8 + 2 = \boxed{10}$ cm.

PUT and TUV are congruent. So TV = 2

Malcolm Rich - 1 year, 10 months ago

if you mean PUT and TUV are similar, then yes

David Vreken - 1 year, 10 months ago

I did mean similar. But it makes the solution much simpler

Malcolm Rich - 1 year, 10 months ago

@Malcolm Rich – I think that's a matter of preference. To prove that $\triangle PUT \sim \triangle TUV$ , you can show that $\angle SUP + \angle PUT + \angle TUV + \angle VUR = 180°$ , and since $\angle SUP = \angle PUT$ and $\angle TUV = \angle VUR$ , $\angle PUT + \angle TUV = 90°$ , which means $\angle PUT = \angle UVT$ , so the triangles are similar by AA similarity. I thought this way was somewhat wordy (unless you know of a better way to show that the triangles are similar), so I used Pythagorean's Theorem instead for a quicker explanation. But both ways will lead to the correct answer.

David Vreken - 1 year, 10 months ago

@David Vreken – I agree. There are many approaches that work. It would perhaps save a few characters recognising that UTVR and PSTU are both "kites" with angles SPT and RUT being identical due to their relationship to SUT.

It's pretty much the same as your explanation but feels to me more elegant.

Malcolm Rich - 1 year, 10 months ago

Tarig Mergani
Jul 23, 2019

Horizontal Curve in Highway Engineering

Red Line = T1 + T2 = R* tan $\frac{D1}{2}$ + R* tan $\frac{D2}{2}$ = 4 * $\frac{8}{4}$ + 4 * $\frac{4}{8}$ = 8 + 2 = 10

T1 = First Tangent , T2 = 2nd Tangent , Di = Deflection Angle

Hassan Abdulla
Jul 23, 2019

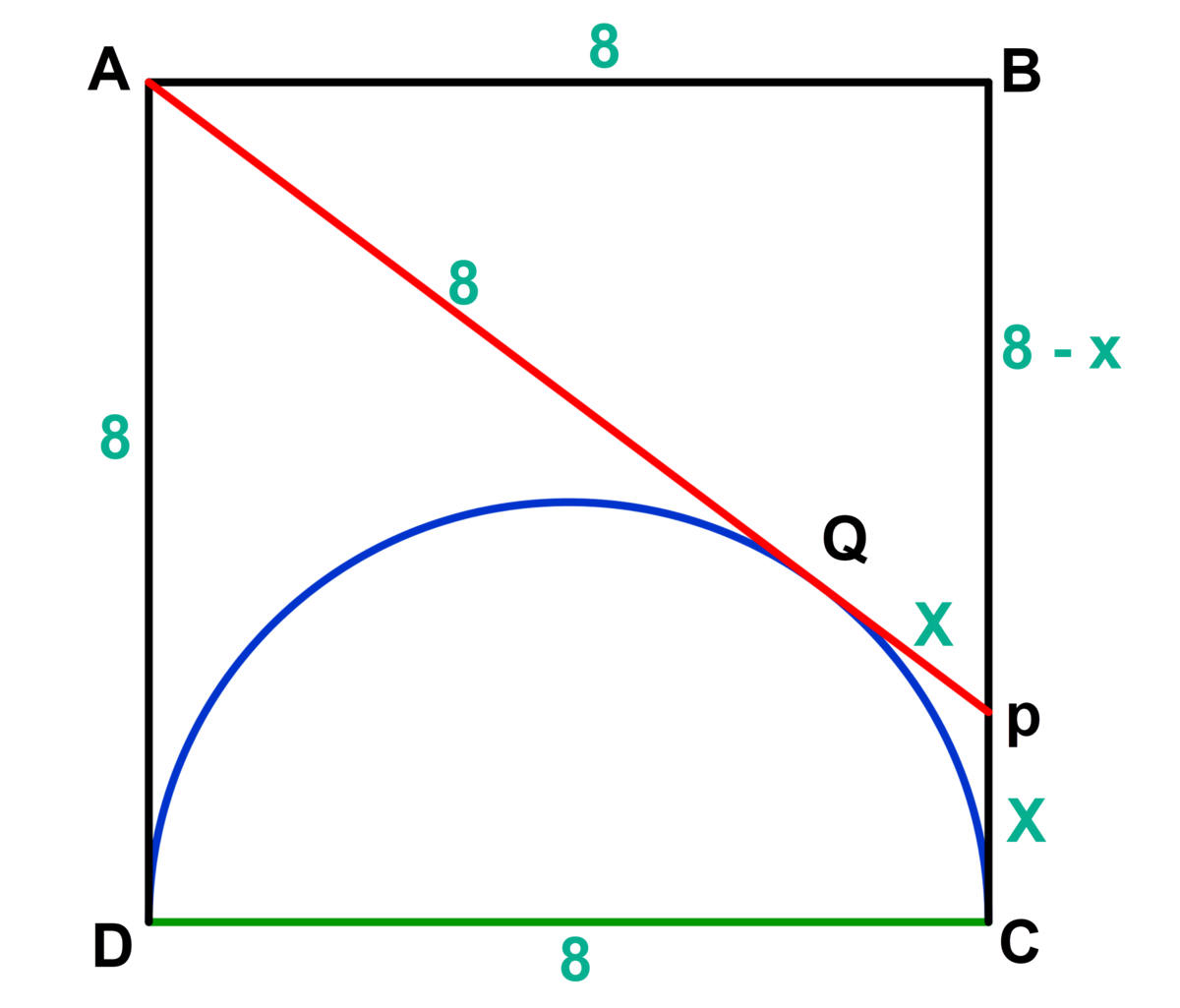
perimeter of the square is 32 cm so each side is 8 cm.

since the tangent lines from same point are equal so AD=AQ and QP=PC=x

$\Delta$ ABP is right angle triangle so $(AB)^2 + (BP)^2=(AP)^2$

$8^2 + (8-x)^2 = (8+x)^2$

so x=2 and AP = 8 + x = 10

Rojo, azul y verde

The answer is 10.

4 solutions

0 pending reports