Rollin' Stones

Let x= $\sqrt[5]{162+27\sqrt[5]{162+27\sqrt[5]{\cdots}}}$ . $\Rightarrow x^5-3^3 x -3^4 \times 2=0$ $\Rightarrow x(\text{i.e radius of bigger circle})=3$ $\color{#D61F06}{Required~Area(A)}\\ =ar(\color{#3D99F6}{trapeziumACDB})-(ar\color{#3D99F6}{(sectorBED)}+ar\color{#3D99F6}{(sectorAEC)})$ $ar(\color{#3D99F6}{trapeziumACDB})=\frac{1}{2}(2\sqrt3)(3+1)$ $ar\color{#3D99F6}{(sectorBED)}=\frac{\frac{\pi}{3}\times 9}{2}$ $ar\color{#3D99F6}{(sectorAEC)}=\frac{\frac{2\pi}{3}\times 1}{2}$ $\Rightarrow A=4\sqrt3-(\frac{3\pi}{2}+\frac{\pi}{3})$ $=4\sqrt 3-\dfrac{11\pi}{2\times 3}$ Hence, a=4, b=3 and c=11 $\Large 4+3+11=\boxed{\color{darkviolet}{\boxed{18}}}$

First we need to find the radius other than $1$ ,

Let,

$x = \sqrt[5]{162+27\sqrt[5]{162+27\sqrt[5]{\cdots}}}$

$x = \sqrt[5]{162+27x}$

$x^{5} -27x -162= 0$

Notice that $x = 3$ satisfy the above equation (I figured it out by mere hit-n-trial),

Hence the two radii are $1$ and $3$ .

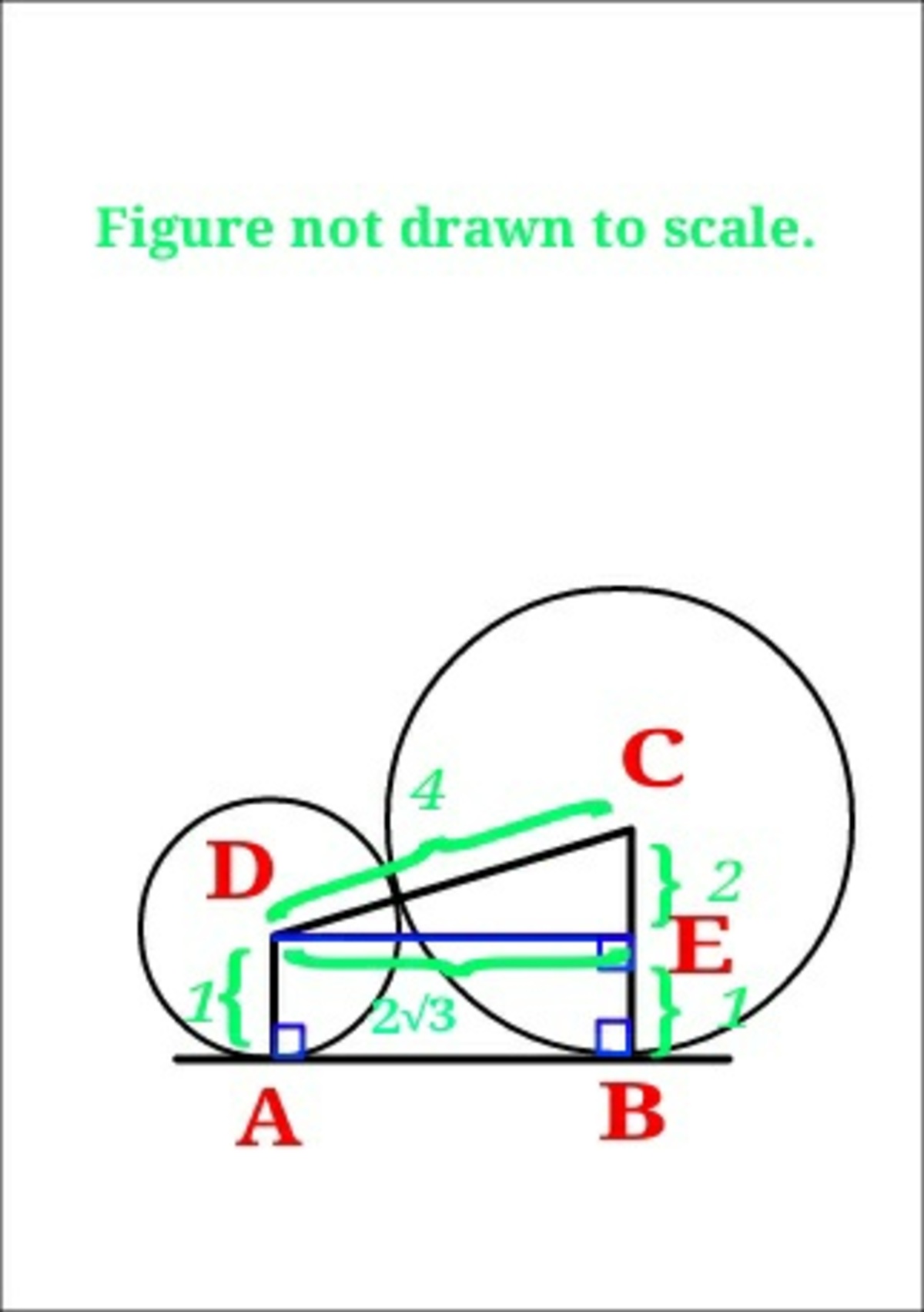
Clearly,

$\angle BCD = 60°$ and $\angle ADC =120°$ .

$area(ABCD) = \frac{(1+3)2\sqrt{3}}{2} \\ area(ABCD) = 4\sqrt{3}$

Now,

$Req.area = area$ $of$ $ABCD- area$ $of$ $two$ $sectors$

$Req.area = 4√3-\frac{1}{6}.\pi(3)^{2}-\frac{1}{3}.\pi(1)^{2}$

$Req.area = 4√3-\frac{11\pi}{6}$

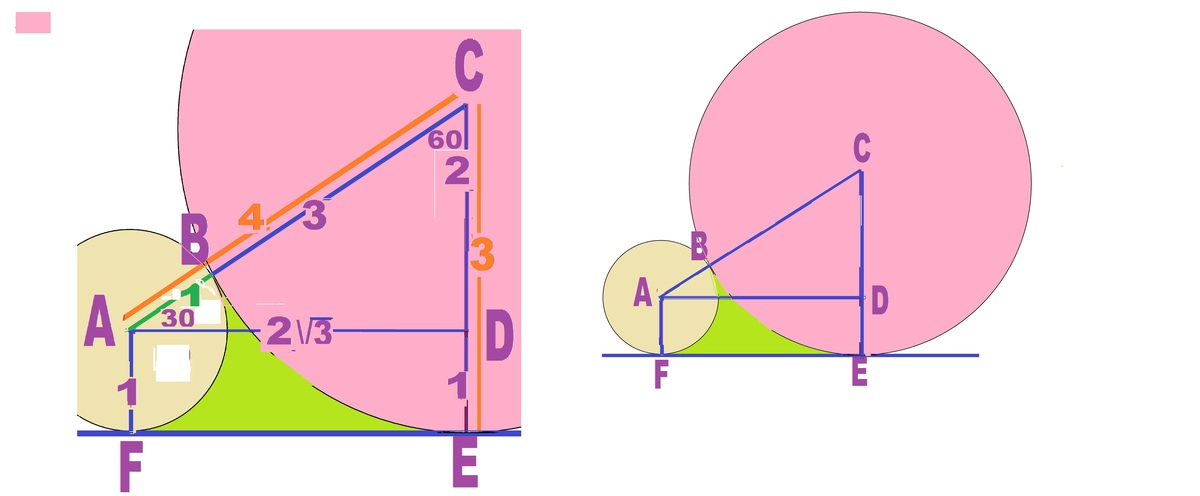
$R=\sqrt[5]{162+27\sqrt[5]{162+27\sqrt[5]{...}}} ~~~~ \implies~(\dfrac R 3)^5 -\frac 1 3 *\dfrac R 3 - 2*\frac 1 3 =0\\ \text{The equation suggests that R= 3 and indeed, R the radius of big circle is 3.}\\ \text{The figure shows the circle BF,r=1, center A, the circle BE,R=3, center C, tangent at B.} \\ \text{The straight line is tangent at F and E. Line joining centers, AC = 4.}\\ Draw ~ AD | | EF, ~ D ~ on ~ CE . ~ CE\bot EF=R=3, ~~ AF\bot EF=r=1=DE. ~~\therefore ~CD=2.\\ \therefore ~\Delta~ACD ~rt. ~ \angle ed ~at ~D, 2CD=AC, ~ the ~ hypotonus. ~~\therefore ~ \angle =CAD=30^o. \\ AD=4*CosCAD=2*\sqrt3. ~~Also ~ \angle BAF=120^o, ~~\angle BCE=60^o.\\ Green~ area~FBE =(Area ~ Trapezium ~ FBCE) - (Sectors ~ 120^o ~ of ~ r=1 ~and~ 60^o ~ of ~ r=3)\\ = AD*(\frac 1 2 CD+ DE) - \pi*(1^2*\frac {120}{360} + 3^2*\frac {60}{360})\\ =4*\sqrt3-\frac{11}6*\pi=4*\sqrt3-\frac{11}{2*3}*\pi \\ Required ~ a+b+c= ~~\boxed{\color{#D61F06}{18}.}$