Rolling Down The Stairs

A solid homogeneous cylinder of mass M = 1 kg and radius R = 2 m rolls down the stairs as shown in the figure below. The height and the width of the steps are both h = 2 0 cm . Assume that the collisions between the cylinder and the steps are inelastic and that the cylinder always remains in contact with the stairs. What will be the terminal velocity (on average) in m/s of the cylinder's center of mass?
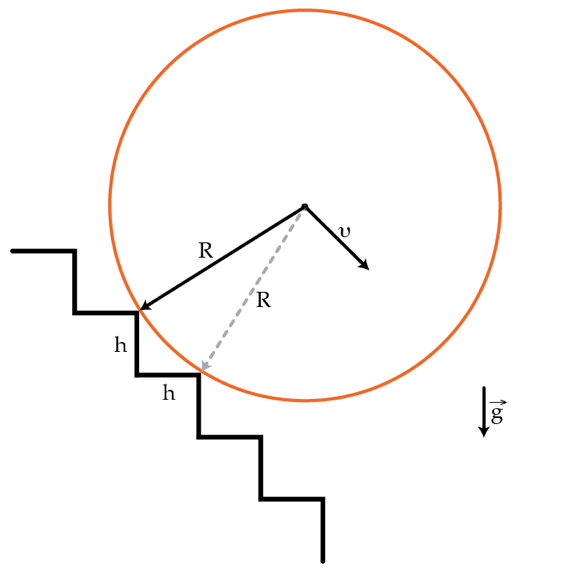
The answer is 13.99.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
r=2, h=0.2
θ = 2 sin − 1 ( 2 r h ) = 0 . 1 4 1 5 r a d
v A = ( 6 2 + 3 2 cos θ ) v f = 0 . 9 9 3 3 v f
with v i = v A ,
4 3 ( v f 2 − v i 2 ) = 0 . 0 1 0 0 v f 2
g r ( sin ( 4 π + 2 θ ) − sin ( 4 π − 2 θ ) ) = 0 . 1 0 0 0 g r
v f 2 = 1 0 . 0 3 3 4 g r = 1 9 6 . 6 5 5 5
v f = 1 4 . 0 2 3 4
v i = 1 3 . 9 2 9 9
every calculation is done on matlab r2014a with 8bytes double type.
i want how the value 11.35 comes. please compare this with solution
Log in to reply
I guess there is a difference between, 2 and 2.000, in that the later, allows u to use all those digits after the decimal, because u are certain. So make v A = 0 . 9 9 v f and so on, and check the value.
Log in to reply
The 2 vs 2.0000 doesn't make a difference. She's using real number types to calculate.
Log in to reply
@Muntasir Sengupta – I was referring to the uncertainty of the measurement.
Log in to reply
@Beakal Tiliksew – what measurement? what are you talking about?
and additionally, i think the term 'average speed' in the problem is ambiguous. in this problem, speed changes from v i to v f periodically. if 'average' means time average, this solution needs more: finding angular speed using angular displacement, integrating inverse-angular speed by theta to find period of this falling-colliding repetation. this problem needs some modification i think
Log in to reply
Yeah, that was what I was saying is straightforward , I felt that it was obvious. but ok i have modified the answer.
I made every equation same to this solution, but my answer didn't work. I checked several times and I think this solution did wrong computation in last part. I think solving last equation gives 14.023. Please check it.
Log in to reply
Try again, with a less significant digit this time,calculating with many uncertain numbers could make a wrong answer.
Log in to reply
I too get the same as Sewoong, I don't think this is an issue of significant digits.
Nice solution
I agree with the method of solution, but the numbers plugged in give ≈ 1 3 . 9 7 m/s!
One small point, it is not possible for v i to equal v A . Other than that point, great solution!
I too had a similar approach but got the wrong answer. I shall recheck my work.
But anyway, thanks a lot for this solution, Beakal. I had been waiting for it for a very long time!!! : )
@ Beakal Tiliksew How you can conserve angular momentum , gravitational torque is acting at the point of contact .
Log in to reply
The conservation of angular momentum is about the stair that is being impacted, during the impact. It's assumed the impact is instantaneous and thus any impulse due to gravity during that time can be neglected. The impulse of the impacted stair cannot change the rotational inertia about the impact point because the force would be crossed with a zero length distance. However, this also assumes that the previous stair does not impart an impulse during impact which may orr may not be true.
Let's analyze what happens when the cylinder collides with the step's edge by using diagram below.
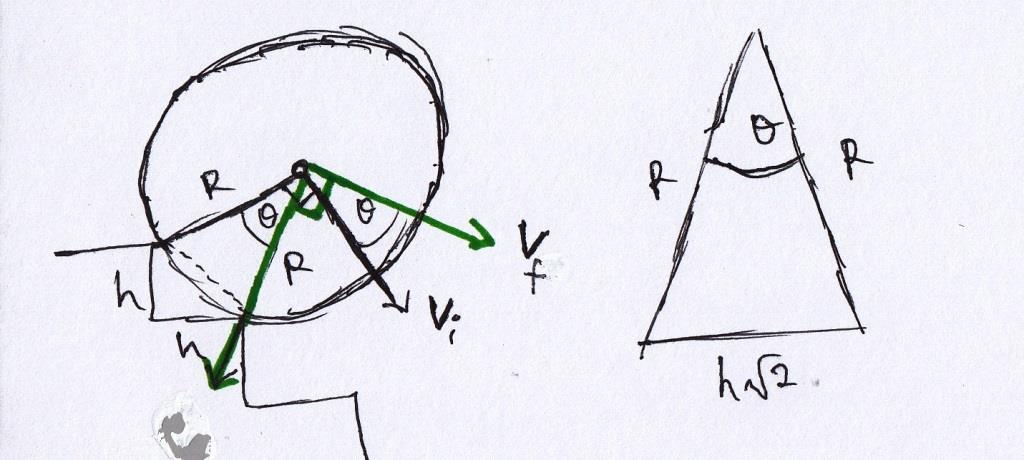 Because the collision is inelastic, the velocity component which passes through the step's edge is reduced to zero, leaving us with only the perpendicular component which can be written as
Because the collision is inelastic, the velocity component which passes through the step's edge is reduced to zero, leaving us with only the perpendicular component which can be written as
v f = v i c o s ( θ )
Cosine law gives
( h 2 ) 2 = R 2 + R 2 − 2 R 2 c o s ( θ ) c o s ( θ ) = 1 − R 2 h 2
Substituting c o s ( θ ) into v f equation, we get
v f = v i ( 1 − R 2 h 2 )
Conservation of mechanical energy (before the cylinder rolls down and right before the collision occurs)
m g h + 2 1 m v 0 2 = 2 1 m v i 2 v i = v 0 2 + 2 g h
The cylinder is in steady-state condition (having terminal velocity), means that velocity after the collision and before it rolls down are the same.
v f = v 0
Substituting all the equations, we have
v 0 2 + 2 g h ( 1 − R 2 h 2 ) = v 0 v 0 = ( 1 − R 2 h 2 ) − 2 − 1 2 g h
Using the fact that h ≪ R , we can apply Taylor's approximation ( 1 + x ) n ≈ ( 1 + n x ) , finally we have:
v 0 = R h g = 1 4 m / s
while conserving the energy of the system why wasn't the rotational kinetic energy of the system taken into consideration?
The best solution ever , legendary , thank you !
Are u assuming friction to be zero
Ok, we shall use the diagram below to analyze the problem ballmovign
Where to begin
ballmovign
Where to begin
Since the cylinder is always in contact with the staircase, through out its motion we will consider the motion of the object pivoted through the edge of the stair.
We have from diagram 1 and 2 , the moment of inertia through the center of mass, and through the pivot point O . I c m = 2 1 m r 2 I O = 2 1 m r 2 + m r 2 = 2 3 m r 2
Also, as the object is moving it has a degree of freedom − 2 θ a n d 2 θ , measured from the 4 5 0 mark, as seen from 3 . The angle θ sweeped out as the object moves from 1 to 3 is given by 2 s i n − 1 ( 2 r h ) .
Looking, at diagram 3 we see that the objects center of mass velocity changes from v f to v A , as it collides with the edge of the stair. This changes is caused by the impulsive forces, at the respective contact points. If we choose our coordinate system, to be at the second contact point, we can avoid doing any calculations which require the change in momentum due to impulsive forces.
So we have
L i = L f ⇒ I c m ω f + m v f r c o s θ = I 0 ω A ⟶ v = ω r
Plugging in the values for the moment of inertia we have,
v A = ( 6 2 + 3 2 c o s θ ) v f
Using conservation of energy during the period of rotation.
2 1 I ω i 2 + m g r s i n ( 4 π + 2 θ ) = 2 1 I ω f 2 + m g r s i n ( 4 π − 2 θ ) ⇒ 4 3 ( v f 2 − v i 2 ) = g r ( s i n ( 4 π + 2 θ ) − s i n ( 4 π − 2 θ ) )
The object has reached terminal velocity when v i = v A ! !
since Δ v ≪ 1 , we have v a v g ≈ 2 v f + v i
Its straightforward from then.