Rolling Semicircle
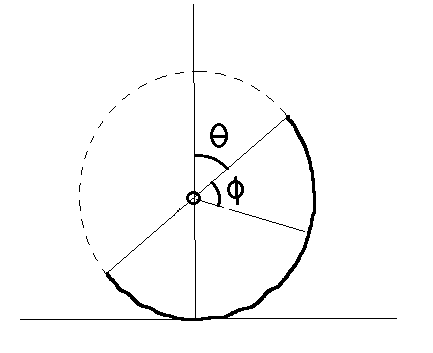
A uniform wire semicircle with a radius of 1 m begins at rest with its diameter vertical (normal to level ground with θ = 0 ). It then rolls back and forth periodically without slipping.
If gravity is 1 0 m/s 2 downward, what is the period of the motion (in seconds)?
Note:
This problem was inspired by a question posed by Azimuddin Sheikh
Note:
The diameter has no associated mass. The line is there for illustration purposes only
The answer is 3.453.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You have the kinetic energy and the potential energy. Since no slipping occurs, the friction force at the point of contact does no work, and so energy is conserved. From this we obtain an expression for θ ˙ in terms of θ alomost immediately, and without all this effort. This makes the period 5 4 ∫ 0 2 1 π cos θ π − 2 cos θ d θ and we evaluate this integral numerically!
Log in to reply
Thank you for posting this alternate approach. Very helpful!
So it is, thanks. Sometimes I go full Lagrange even when COE would suffice.
@Mark Hennings sir can u pls show how u get that integration by using energy equation? I would have post mine energy equation and just ask for correctness but here no latexifying technique is there so asking u sir ,pls show sir how using energy equation , and above expression would lead to elimination of dtheta/dt .
Log in to reply
Conservation of energy tells us that π M R 2 θ ˙ 2 [ π − 2 sin θ ] + π M g R [ π − 2 sin θ ] = π M g R and so θ ˙ = ± R ( π − 2 sin θ ) 2 g sin θ where the choice of sign depends on which way the wire is rolling. Separating variables, the period is T = 2 ∫ 0 π 2 g sin θ R ( π − 2 sin θ ) d θ which is basically the same as my formula.
Log in to reply
@Mark Hennings – Thx a lot sir . between @Mark Hennings sir can u help in collisions problem I posted in discussion section pls.
This is what I did bcuz i was lazy:
It is likely that the period would vary depending on the initial angle the wire is stood on (initial θ ). But since I was lazy, I assumed that the initial angle is small. θ ∼ 0 . The c.g. of the wire lies c = π 2 away from the center of the semicircle. Say the angle the wire is standing at angle θ . Then the torque generated by both the weight and normal force would be τ = m g θ c = m g θ π 2 , assuming small t h e t a and where m is the mass of the wire. The moment of inertia about the contact point between the wire and ground is I = 2 m . Hence the angular acceleration θ ′ ′ = I t a u = π g θ = k θ . Hence the period of oscillation is k 2 π = 5 2 π 3 ∼ 3 . 5 2
This differs from Steven's answer due to the initial angle (mine being close to 0 and Steven's being 2 π .
How did you get the moment of inertia there? Steiner's theorem?
In all the steps shown below, M = 1 kg, and R =1m.
In the plot, the unit of angular displacement is in radians. I have left out some steps in this solution. If necessary, I will add them later. I do not usually post solutions here so please do point out any mistakes/typos.
Thanks for the solution. I posted mine as well. Looks like we're basically on the same page
Suppose that the semicircle begins upright ( θ = 0 ), with the center of the diameter at x = 0 . The semicircle then proceeds to roll without slipping.
Coordinates of center of diameter (which would be the center of the circle if the circle was full):
x C = R θ y C = R
Coordinates of a point on the semicircle ( θ is effectively our state variable; each point has a constant ϕ ):
x = R θ + R s i n ( θ + ϕ ) y = R + R c o s ( θ + ϕ ) x ˙ = R θ ˙ + R θ ˙ c o s ( θ + ϕ ) y ˙ = − R θ ˙ s i n ( θ + ϕ )
Velocity of a point on the semicircle:
v 2 = x ˙ 2 + y ˙ 2 = 2 R 2 θ ˙ 2 + 2 R 2 θ ˙ 2 c o s ( θ + ϕ )
Infinitesimal mass:
d m = M π d ϕ = π M d ϕ
Infinitesimal kinetic energy:
d E = 2 1 d m v 2 = 2 1 π M d ϕ [ 2 R 2 θ ˙ 2 + 2 R 2 θ ˙ 2 c o s ( θ + ϕ ) ] = π M R 2 θ ˙ 2 [ 1 + c o s ( θ + ϕ ) ] d ϕ
Total kinetic energy:
E = π M R 2 θ ˙ 2 ∫ 0 π [ 1 + c o s ( θ + ϕ ) ] d ϕ = π M R 2 θ ˙ 2 [ π − 2 s i n θ ]
Infinitesimal gravitational potential energy:
d U = d m g y = π M g d ϕ [ R + R c o s ( θ + ϕ ) ] = π M g R [ 1 + c o s ( θ + ϕ ) ] d ϕ
The gravitational potential energy integral is the same as the kinetic energy integral, except for the constant:
U = π M g R [ π − 2 s i n θ ]
System Lagrangian:
L = E − U = π M R 2 θ ˙ 2 [ π − 2 s i n θ ] − π M g R [ π − 2 s i n θ ]
Equation of motion:
d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L
Evaluation step one:
∂ θ ˙ ∂ L = π 2 M R 2 θ ˙ [ π − 2 s i n θ ]
Evaluation step two:
d t d ∂ θ ˙ ∂ L = π 2 M R 2 [ θ ˙ ( − 2 c o s θ θ ˙ ) + θ ¨ ( π − 2 s i n θ ) ] = − π 4 M R 2 c o s θ θ ˙ 2 + 2 M R 2 θ ¨ − π 4 M R 2 s i n θ θ ¨
Evaluation step three:
∂ θ ∂ L = π M R 2 θ ˙ 2 [ − 2 c o s θ ] − π M g R [ − 2 c o s θ ] = − π 2 M R 2 θ ˙ 2 c o s θ + 2 π M g R c o s θ
Equating:
− π 4 M R 2 c o s θ θ ˙ 2 + 2 M R 2 θ ¨ − π 4 M R 2 s i n θ θ ¨ = − π 2 M R 2 θ ˙ 2 c o s θ + 2 π M g R c o s θ 2 M R 2 θ ¨ − π 4 M R 2 s i n θ θ ¨ = π 2 M R 2 θ ˙ 2 c o s θ + 2 π M g R c o s θ R π θ ¨ − 2 R s i n θ θ ¨ = R θ ˙ 2 c o s θ + g c o s θ
Final result:
θ ¨ = R π − 2 R s i n θ R θ ˙ 2 c o s θ + g c o s θ
Here is a plot of theta vs time (generated from numerical integration) for a semicircle diameter of 2 meters. The period is about 3.453 seconds, which seems reasonable for an object of that size. You can see that it rocks back and forth between θ = 0 (standing on one end of the diameter) and θ = π (standing on the other end).