Rolling the square root graph
The graph of f ( x ) = x over the interval [ 0 , 1 ] is rolled on the y -axis.
What are the destination coordinates ( x 0 , y 0 ) of the lower tip, which was originally at ( 0 , 0 ) ?
Submit ⌊ 1 0 0 0 ( x 0 + y 0 ) ⌋ as your answer.
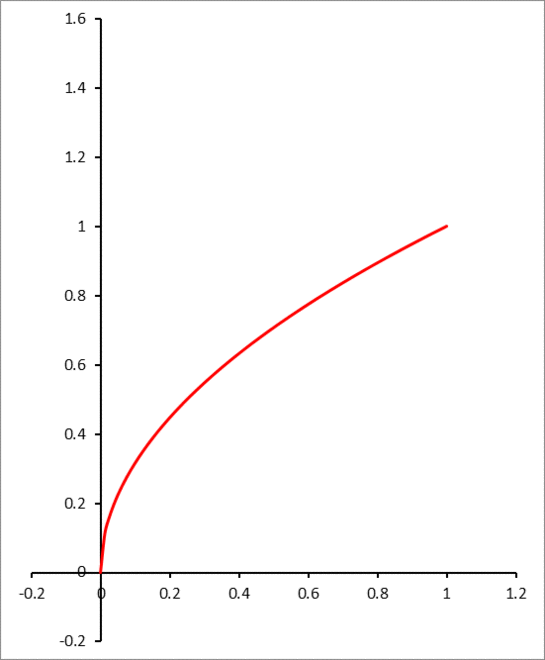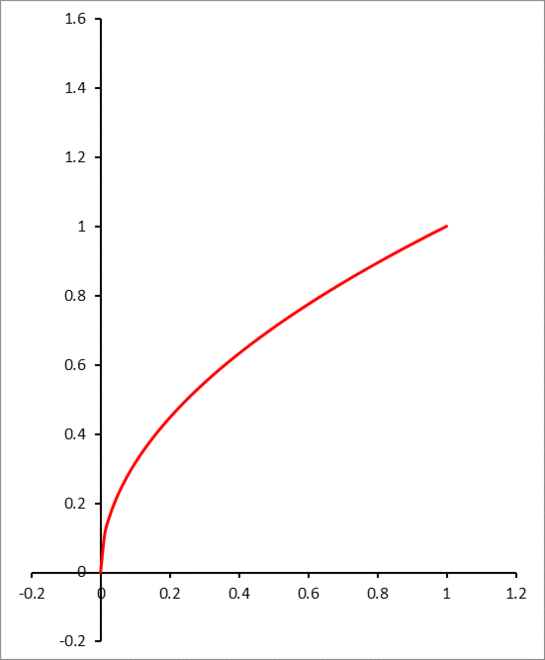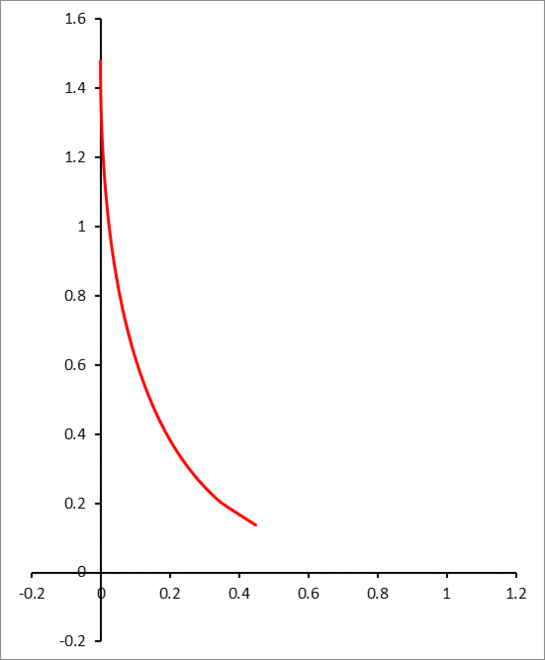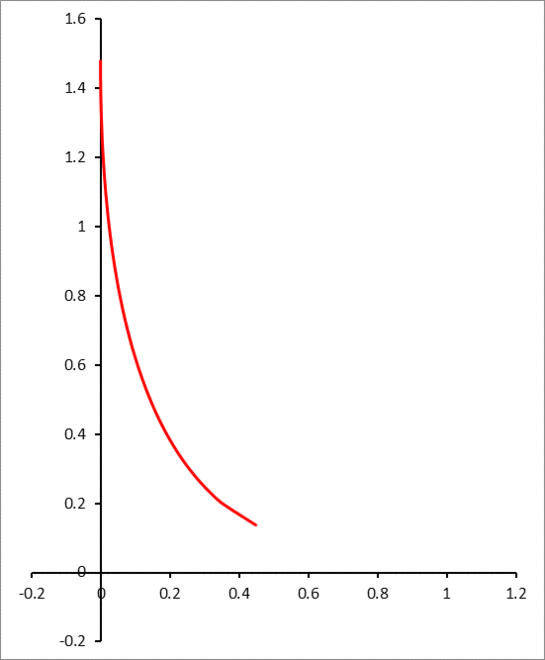
The answer is 584.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Great solution!👍👍👍
What if u consider rectangle
Let's consider the initial position of the graph, the tangent at ( 1 , 1 ) will roll into the y-axis at the point ( 0 , L ) , where L is the length of the curve. When we roll the curve along the y-axis, we're basically applying a rotation and shifting to the frame ( x , y ) . Let's call the final frame O x ′ y ′ , then
( x ′ , y ′ ) = d + R ( x , y )
where R is a rotation matrix, the angle of rotation is θ = 2 π − ϕ , where ϕ is the angle that the tangent at ( 1 , 1 ) makes with the x-axis, that is, ϕ = tan − 1 ( 2 1 ) ,
from which sin θ = cos ( tan − 1 ( 2 1 ) ) = 1 + 4 1 1 = 5 2 , and cos θ = 5 1 . Thus, matrix R is given by,
R = [ cos θ sin θ − sin θ cos θ ] = ⎣ ⎢ ⎡ 5 1 5 2 − 5 2 5 1 ⎦ ⎥ ⎤
To find the vector d in the equation relating ( x , y ) and ( x ′ , y ′ ) , we substitute the point ( x , y ) = ( 1 , 1 ) and the corresponding point ( x ′ , y ′ ) = ( 0 , L ) . The curve length L is given by,
L = ∫ 0 1 1 + 4 y 2 d y = 4 1 ( 2 5 + ln ( 2 + 5 ) ) = 1 . 4 7 8 9 4 2 8
It follows that
d = ( 0 , L ) − R ( 1 , 1 ) = ( 0 , 1 . 4 7 8 9 4 2 8 ) − ( − 5 1 , 5 3 ) = ( 0 . 4 4 7 2 1 3 6 , 0 . 1 3 7 3 0 2 0 1 3 5 )
And therefore, the final destination coordinates of the point that was originally at ( 0 , 0 ) are
( x 0 , y 0 ) = d + R ( 0 , 0 ) = d = ( 0 . 4 4 7 2 1 3 6 , 0 . 1 3 7 3 0 2 0 1 3 5 )
making the answer, ⌊ 1 0 0 0 ( x 0 + y 0 ) ⌋ = 5 8 4
Wow, another endearing and charming problem! How do you come up with this stuff?!
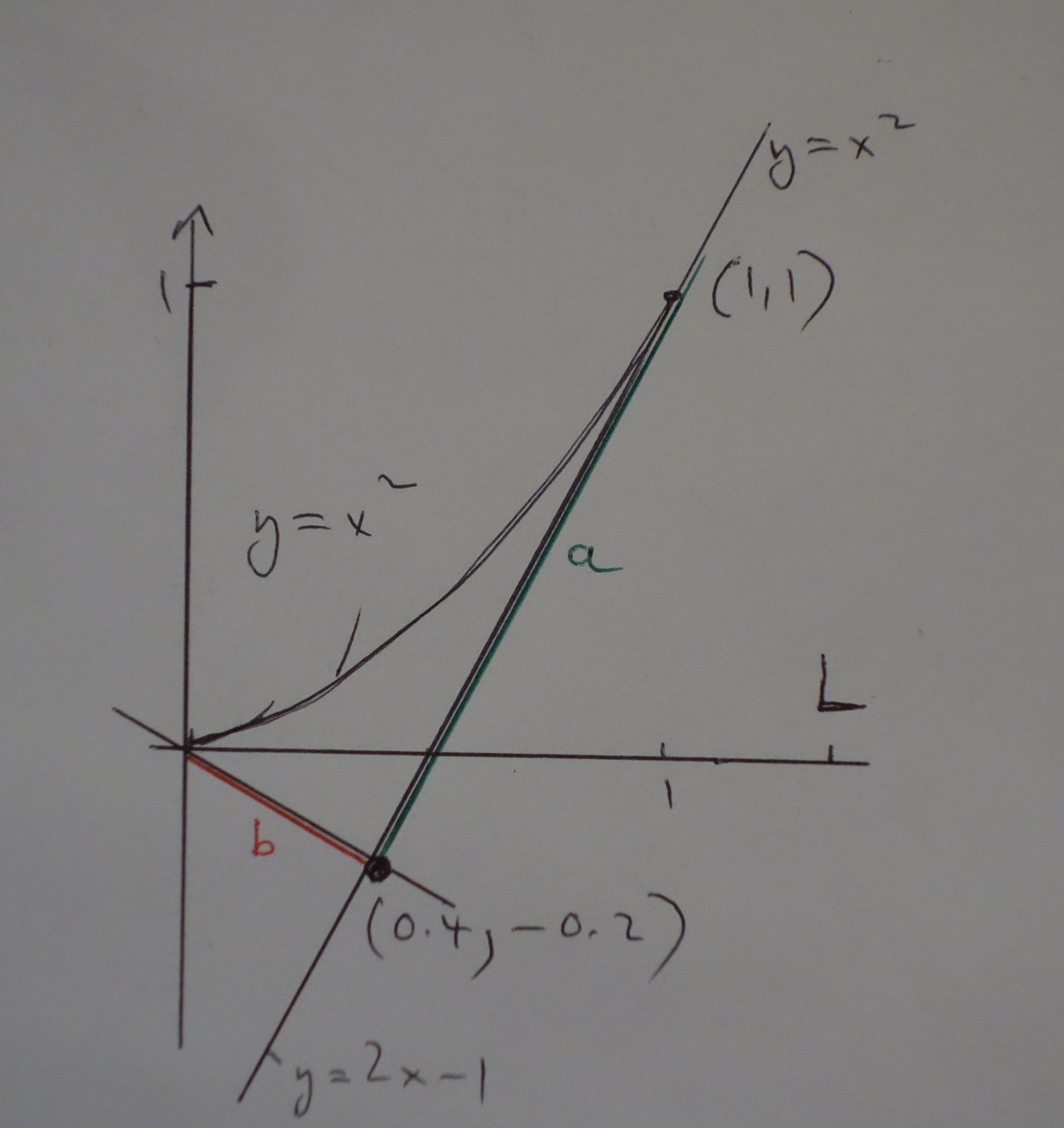
The problem itself is not hard at all, which makes it even more delightful. For psychological reasons, I rather work with the square graph than with the square root, reflection across the diagonal of the first quadrant. With the notations introduced in the attached figure, the point we seek is ( x , y ) = ( L − a , b ) . Now a and b are just distances, and the arc length is L = ∫ 0 1 1 + 4 x 2 d x ≈ 1 . 4 7 8 9 4 . My calculator tells me that ⌊ 1 0 0 0 ( x + y ) ⌋ = 5 8 4 .
One way of solving the problem is by decomposing the roll movement into a rotation and a displacement. Such movement would have two nice properties:
- The angle of rotation would be such that the tangent line of the curve in the upper tip is now the y axis.
- The upper tip would end up in the coordinate ( 0 , l ) where l is the length of the curve from 0 to 1.
To easily calculate such transformations we can use complex algebra. By doing this, the rotation would be a multiplication and the displacement an addition. Rewriting the two properties above explicitly:
- c o t a n ( θ ) = d x d x ∣ ∣ ∣ x = 1
- ( 1 + i ) [ c o s ( θ ) + i s i n ( θ ) ] + x 0 + y 0 i = i l = i ∫ 0 1 1 + ( d x d x ) 2 d x
Solving the first equation we obtain that c o t a n ( θ ) = 2 1 ⇒ c o s ( θ ) = 5 1 , s i n ( θ ) = 5 2 . Plugin in the second equation and by solving the integral:
( 1 + i ) ( 5 1 + i 5 2 ) + x 0 + y 0 i = 8 i [ 4 5 + l n ( 9 + 4 5 ) ]
Finally we can solve for the real and imaginary parts independently obtaining the following displacement coordinates:
- x 0 = 5 1
- y 0 = 8 1 [ 4 5 + l n ( 9 + 4 5 ) ] − 5 3
The solution is thus: ⌊ 1 0 0 0 ( 8 1 [ 4 5 + l n ( 9 + 4 5 ) ] − 5 2 ) ⌋ = 5 8 4
Shouldn't we rotate anticlockwise by (pi/2 - theta) using cis(pi/2 - theta) rather than cis(theta)?
Log in to reply
Read carefully, I used the cotangent instead of the tangent when defining theta. In doing so, I avoid setting the angle, say phi, that would correspond to the theta you used in your comment, and then defining my theta as the complement of that phi.
In other words, I need to rotate counterclockwise by the complement of the angle that the tangent line at x = 1 makes with the x-axis. This is achieved by turning counterclockwise by a theta angle whose cotangent is the value of the derivative of the function at x = 1.
That's taken into account by using the cotangent instead of the tangent. Both methods are equivalent since tan ( π / 2 − x ) = cotan ( x )
For the arc length we use the formula L = ∫ 0 1 1 + ( g ′ ( x ) ) 2 . For ease we do not use f = x , but its inverse g = x 2 instead. ∫ 0 1 1 + 4 x 2 d x = 2 1 ∫ 0 2 1 + u 2 d u = 2 1 ∫ 0 a r c s i n h ( 2 ) 1 + ( sinh ( t ) ) 2 d sinh ( t ) = 2 1 ∫ 0 a r c s i n h ( 2 ) cosh 2 ( t ) d t = 4 t ∗ + 8 sinh ( 2 t ∗ ) evaluated at t ∗ = a r c s i n h ( 2 ) , which gives L = 1.4789...
The point (1,1) is on the line y=x at distance 2 from the origin, and the graph makes an angle α = a r c t a n ( 1 ) − a r c t a n 2 1 with that line. Doing some trig, we see our point will be at ( 2 sin ( α ) , L − 2 cos ( α ) ) which is appoximately at (0.4472, 0.1373), so that the required answer is 584.
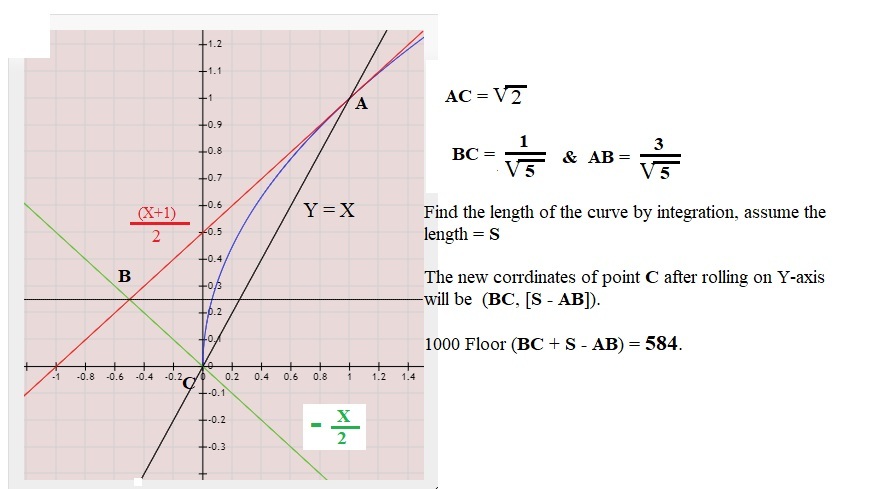
Find the two lines, first line:
(1) y=(1/2)(x+1), tangent at (1,1) to curve y=√x,
and second line
(2) y=-2x-0.30692,
perpendicular to tangent line at distance 1.4789 ( length of curve) away at (-0.322768, 0.338616).
Find the distance of (0,0) to above two lines as (0.44721, 0.137258),
Answer=1000(0.44721+0.137258)=584
How did you find these decimal numbers? Are they exact?
Log in to reply
Decimal numbers are from calculator and/or WolframAlpha.
For instance, the first decimal number is length of the curve 1.4789 and this (not exact) is from integration by WolframAlpha.
The remaining decimal numbers get generated from this curve length dependent calculations. We can't just avoid them?
Log in to reply
What are the expressions/figures you need to get these numbers? I don't know how you generated these numbers. Can you elaborate on them?
Log in to reply
@Pi Han Goh – Curve length of 1.4789 between (0,0) and (1,1) on y=√x is obtained from integration of dx√(1+(dy/dx)^2 from 0 to 1 using WolframAlpha.
Point (-0.322768, 0.338616) is generated as a point 1.4789 away on line y=(1/2)(x+1) from point (1,1).
Later, the line perpendicular to first line is y=-2x+c, where c=-0.30692 is calculated as point (-0.322768, 0.338616) lies on this line.
Finally, (0.44721, 0.137258) are perpendicular distances of (0,0) from line 1 & 2.
I have used standard geometrical expressions in each of these calculations.
First let's get some measurements of y = x before its roll. Let O be the endpoint at the the origin, let A be the endpoint at ( 1 , 1 ) , let A B be the tangent to y at A , and let B be on the y -axis, as shown below:
Since A is at ( 1 , 1 ) , by Pythagorean's Theorem, A O = 1 2 + 1 2 = 2 . The slope of A O is 1 1 = 1 , so its angle of inclination is tan − 1 1 = 4 5 ° , which means ∠ A O B = 9 0 ° − 4 5 ° = 4 5 ° .
Also, d x d y = 2 x 1 , so the slope of y at A ( 1 , 1 ) (and also the slope of A B ) is m = 2 1 1 = 2 1 , so its angle of inclination is tan − 1 2 1 , which means ∠ A B O = 9 0 ° + tan − 1 2 1 . From the triangle sum of △ A B O , ∠ B A O = 1 8 0 ° − 4 5 ° − ( 9 0 ° + tan − 1 2 1 ) = 4 5 ° − tan − 1 2 1 .
The arc length from A to O is s = ∫ 0 1 1 + ( d x d y ) 2 d x = ∫ 0 1 1 + ( 2 x 1 ) 2 d x ≈ 1 . 4 7 8 9 4 .
After the curve is rolled, △ A B O is mapped to △ A ′ B ′ O ′ , where A ′ B ′ is on the y -axis, and A is at ( 0 , 1 . 4 7 8 9 4 ) . Let C ′ be on the y -axis such that ∠ A ′ C ′ O ′ is a right angle, as shown below:
Then A ′ O ′ = A O = 2 and ∠ C ′ A ′ O ′ = ∠ B A O = 4 5 ° − tan − 1 2 1 , and by trigonometry A ′ C ′ = 2 cos ( 4 5 ° − tan − 1 2 1 ) ≈ 1 . 3 4 1 6 4 , and O ′ C ′ = 2 sin ( 4 5 ° − tan − 1 2 1 ) ≈ 0 . 4 4 7 2 1 .
Therefore, the coordinates of O ′ are ( 0 . 4 4 7 2 1 , 1 . 4 7 8 9 4 − 1 . 3 4 1 6 4 ) or ( 0 . 4 4 7 2 1 , 0 . 1 3 7 3 0 ) , so x 0 = 0 . 4 4 7 2 1 and y 0 = 0 . 1 3 7 3 0 , and ⌊ 1 0 0 0 ( x 0 + y 0 ) ⌋ = 5 8 4 .