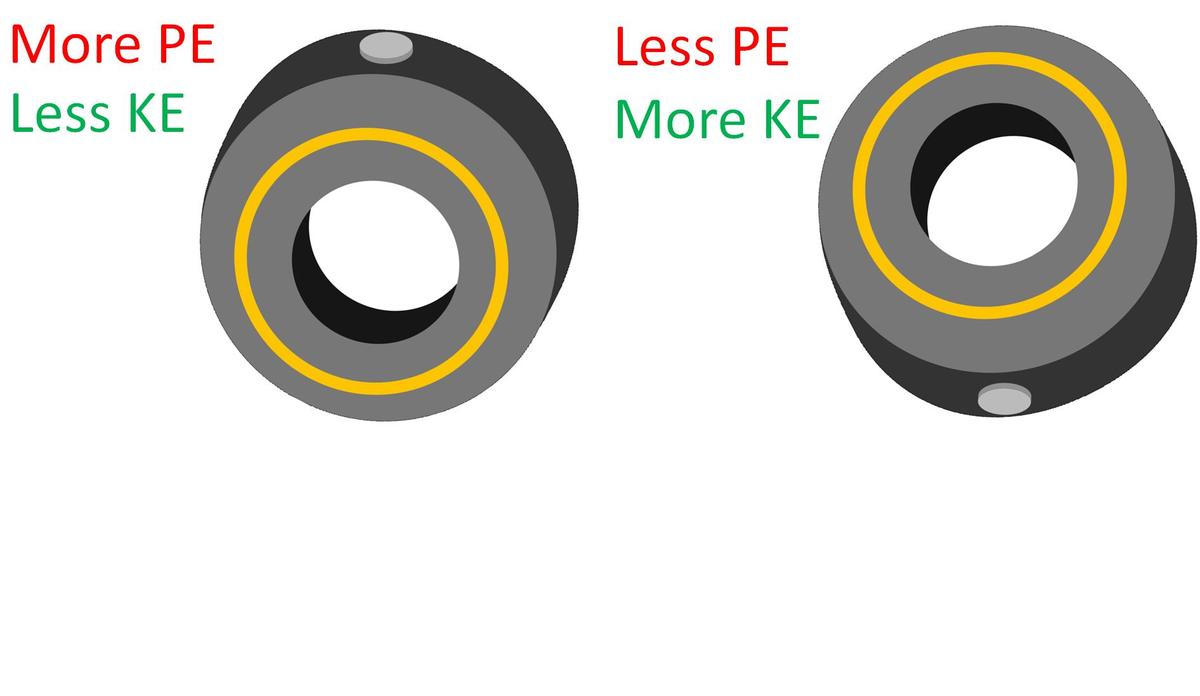
Rolling with a bead
A large nail is stuck in a tire, which is set in motion and left to roll on its own. Assuming there is sufficient friction for the tire to roll without slipping, what best describes the motion of the tire?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
This answer is wrong. The nail is actually standing still when it is at the bottom and touching the road and it has near 0 kinetic energy. Since at the bottom point the nail has the least kinetic energy and the least potential energy, the rest of the tire has the most kinetic energy (in its cycle) and the tire has no differences in potential energy during the cycles. Ergo the tire moves fastest then.
Log in to reply
I agree with you that it is not the kinetic energy of the nail but the nail plus tire system. The solution seems to be updated.
Log in to reply
Yeah, it was updated. It still isn't a complete proof, but it's not outright wrong any more.
then u explain it bruh
Log in to reply
Dabber I did explain it both here and in my own solution/answer below. This answer was changed/fixed after my comment, probably because he realized I was right.
Log in to reply
@Komninos Maraslidis – *she
and btw I didn't change anything. it changed itself somehow.
Log in to reply
@Laura Gao – LOL that's strange.
Maybe the admins were embarrassed that the top voted by far solution was technically erroneous.
The answer is wrong! As a hypothesis consider the mass of the nail as it traverses the perimeter of the tire while in motion. You are viewing the tire (as a face of a clock ), as the tire rolls counterclockwise. If at the 9 o'clock position, the nail exerts an additional one unit of force downward, while at the 3 o'clock position, the nail exerts a -1 unit of force as it is pulled upward. Since the question is about the overall movement of the tire and not about potential kinetic forces during one particular cycle of travel, then the overall motion of the tire will remain constant unless external forces are applied, changing the scenario.
You are saying that the nail in the tire actually changes the massive engine and drive train that moves the tire.
Log in to reply
The tire is not attached to a engine or a motor. It is rolling and is free to move on its own.
You’re ignoring the fact the the nail head has height, so the tyre loses kinetic energy and gains potential energy as it lifts over the nail.
Log in to reply
The height of the nail head is small compared to the radius of the tire, so it does not result in much decrease of the kinetic energy. Also, the nail lifts the tire for a very small period of time.
Log in to reply
The mass of the nail is also small in comparison to the tire. So seeing all of these comments, the question really feels like "Does the small mass of the nail or the short height of its protrusion cause more of an effect on the momentary speed of the tire when the nail is exactly at the bottom?". When I answered the question I visualised a teardrop shaped object because I assumed the height of the nail was the variable in question. When you set a teardrop shaped object in motion it decelerates as it comes to the pointed end, reaches its slowest at the point of the teardrop, then accelerates to its fastest at some point along its circular arc. In other words, when the nail is at the bottom and lifts up the tire, some of the kinetic energy of the tire is converted into potential energy because of its new elevation. Conversely you could argue for a different visualization: imagine a doughnut with it's hole slightly off center, leaving more mass at end than the other. When we set this object in motion it accelerates until most of its mass is at the bottom, at which point it moves fastest, and then decelerates until it's mass is at the top, where it moves the slowest. The kinetic energy is highest then the most mass (the nail) is at the bottom. These visualizations are contradictory with each other. Therefore the height of the nail and the mass of the nail matter as factors in determining the answer. Is the conversion from KE to PE (due to the height of the nail head when it lifts the tire up) greater or less than the increase in KE of the tire if the nail's mass is at the bottom?
Log in to reply
@Benjamin Sawyers – Your imagination is a bit too out of context (of a simple physics problem), but they could have put the nail on the inside of the tire or on the side so it wouldn't bounce the tire.
Log in to reply
@Komninos Maraslidis – That's absolutely right. The concepts are simple, but the question could be clarified. It's the difference between labeling a color brown vs. labeling it burnt ochre. As long as the concepts and the variables are correctly identified, understood, and applied, then I'm not worried about splitting hairs either. That's what brilliant is all about anyway, gaining a deeper understanding of how things genuinely work. So cheers, Maraslidis, for pushing yourself to think deeply and clearly.
The answer is wrong! As a hypothesis consider the mass of the nail as it traverses the perimeter of the tire while in motion. You are viewing the tire (as a face of a clock ), as the tire rolls counterclockwise. If at the 9 o'clock position, the nail exerts an additional one unit of force downward, while at the 3 o'clock position, the nail exerts a -1 unit of force as it is pulled upward. Since the question is about the overall movement of the tire and not about potential kinetic forces during one particular cycle of travel, then the overall motion of the tire will remain constant unless external forces are applied, changing the scenario.
Log in to reply
You're missing the point of the question. "Since the question is about the overall movement of the tire and not about potential kinetic forces during one particular cycle of travel" The question is precisely about the differences of rotation speed during a single cycle.
Log in to reply
Based on the wording of the question, I would contend that a case could be made for both perspectives.
Log in to reply
@Michael Reichwein – Not if you parse English correctly and read the possible answers too.
Log in to reply
@Komninos Maraslidis – The first two answer options are poorly or ambiguously phrased. How can you measure
Log in to reply
@R S – I personally believe that the effects of increase in kinetic energy as a result of the increase in the gravitational pull based on mass of such miniscule proportions, would not immeasurably effect the speed or rotation of the tire (even though course of one cycle)! I find it analogous to dumping a gallon of water into the Dead Sea and then claiming it has a lower salt content!
Log in to reply
@Michael Reichwein – It does though. It's like you guys haven't ever taken a course of "idealistic" high-school physics.
@Komninos Maraslidis – If it was worded correctly there would have been less comments concerning the wording on this thread
They should have phrased it differently. Saying "the tire moves faster when the nail is at the bottom" makes it sound like it's accellerating when the nail is at the bottom. "The tire is faster while the nail is at the bottom" would be better.
The question is poorly phrased. When it reaches the top it is slowest and the accelerates down to the bottom where it starts to slow down. I reject my “incorrect” answer.
Wouldn't the height of the nail head push the tire up resulting in the conversion of some kinetic energy to potential energy? I realise the height of the nail is small in comparison to the diameter of the tire, but so is the mass of the nail in comparison to the mass of the tire.
There are two ways to visualize this problem: 1) Imagine a teardrop shape set in motion on a 2d plane. That teardrop decelerates as it comes to the pointed end, reaches its slowest at the point of the teardrop, then accelerates to its fastest at some point along its circular arc. In other words, when the nail is at the bottom and lifts up the tire, some of the kinetic energy of the tire is converted into potential energy because of its new elevation. 2) Imagine a doughnut shape on a 2d plane with it's hole slightly off center, leaving more mass at end than the other. When we set this object in motion it accelerates until most of its mass is at the bottom, at which point it moves fastest, and then decelerates until it's mass is at the top, where it moves the slowest.
In visualization one, the point of the teardrop shape represents the nail, and the object is SLOWEST when that point is at the bottom.
In visualization two, the thickest end of the doughnut represents the nail, and the object is FASTEST when that end is at the bottom.
Because these two visualizations are contradictory, we must appreciate that both the mass and height of the nail have some effect on the speed of the tire. The values of these variables matter in determining the answer; and in its current state the question seems to be short of enough information to have a direct answer.
Note to author of question: In order to clarify and keep the same answer correct, consider including that the nail head has zero thickness or that the nail is completely buried into the face of the tire.
Cheers,
The nail is 100g, for example. The pull of gravity is more than 100g. The total weight of the nail and tyre is unknown. The gravitational pull is unknown. There is a problem in the question.
Log in to reply
not really, because the tire is symmetrical.
I'm pretty sure that the weight of the nail can be ignored... have ever the autor of this question tried to lift a tire?
Log in to reply
the question says 'a large nail is stuck in a tire'
Log in to reply
It would have to be a VERY large nail to influence that mass. I agree... it’s not a well worded question. I dislike mixing “theoretical” and “real world” because many times the answer is - it has no impact.
I think the first two answer options may be poorly or ambiguously phrased, leading to unintended confusion. Replacing the words "when" with "as" and "is at" with "as it approaches" may help.
However, unless the nail has no thickness, it would increase the relative radius at that point. Some of the forward motion would be used to lift the wheel as the nail hits the ground. This slows the wheel, which then speeds up as the nail is lifted off the ground and the wheel can move downwards. (Think of a camshaft) So the answer would be that motion is faster while the nail is at the top and slower while it is at the bottom.
This question is really perfect to understand conservation of energy in rolling motion.
-
So, instead of taking ground as the reference frame, I am starting to run with the same horizontal linear velocity as the ring. Then relative to me the ring is only rotating (not rolling).
-
Now, when the nail is at the top it has maximum potential energy. But when the nail reaches the bottom of ring (i.e. wheel), the kinetic energy is maximum (for the sake of conservation of energy).
-
Due to the maximum value of K.E. the velocity of the nail is maximum at this point (along tangential direction w.r.t me). Hence, the momentum of nail is also maximum at this point, which is instantaneously transferred to the wheel.
-
Due to this instantaneous transfer of momentum. The wheel too has maximum velocity when the nail is at bottom.
work required to move the nail to the top is greater at the bottom since gravity moves the nail down from top to bottom with fewer N required for the work. Also, the nail would have increased friction at the bottom which isn't present at the top.
Log in to reply
What is the direction of friction when the nail is moving down from the top?
Log in to reply
There is no rolling friction described in the problem. The only friction given is the static friction on the point of contact required to make the tire roll instead of slide. That friction produces no work/energy because the velocity is 0 at that point (work=force X velocity). In reality the contact is not a point but a surface area and there are lots of factors to consider, but this is a simplified problem, not an engineering model.
Wait a sec, when the nail is at the bottom, doesn't it bump the wheel up, which loses kinetic energy?
Log in to reply
...mmm....it also depend on what is rolling...assume an highspeed road...rubber has a specific coefficient of adherence....the nail had will reduce that when hitting the road...
The nail is properly embedded in the tire surface and does not create any significant bump to consider.
See if there is a bump it will de facto experience a jump.
Ignore the following. I read the question too quickly and thought it was asking about the motion of the nail not the speed of tire and nail as a whole. 1. Relative to the center, all points on the perimeter of the wheel have the same angular and linear speed. 2. The nail is in contact with the road at the bottom and if the tire/nail is not slipping on the road then the contact point of the tire has the same speed as the road. The nail is instantaneously at rest at the bottom. 3. If the speed were larger at the bottom then in wet conditions water would “fly off” the rolling (not slipping) wheel at the bottom. This is not what happens and it is why your back gets wet when riding a bicycle on a wet road.
I guessed What does K.E mean? What does P.E stand for? How does this work? I would rate this problem a 10 because l don't really understand it
Log in to reply
KE means kinetic energy and PE means potential energy.
Because the tire is left to roll on its own and friction is not doing any work, its total energy is conserved. When the nail is at the bottom most point the potential energy of the nail plus tire system is minimum and the kinetic energy is maximum.
The choices were very vague, The possible answer should state choice 1: The tire moves faster when the nail is going from bottom to top choice 2: The tire moves faster when the nail is going from top to bottom.
My understanding is that it will be faster when the nail is at the top because due to gravity it will gain velocity while going down. Which got me wrong because the possible answers were very vague and does not explain well. my 2 cents.
Log in to reply
I think the options are fairly clear. When the nail is at the bottom most point the speed of the tire is greatest.
Log in to reply
it does not makes sense, i have a different perception of the choices. other people may perceive the same.
Log in to reply
@Renemar Sultones – The problem is that you tie the word "faster" with acceleration. Perhaps they should have used "fastest", but most people already understand what it means.
This answer makes a mistake in that it thinks you can change the reference frame from the ground to the "same horizontal linear velocity as the ring". It is not another inertial frame of reference and the answer even "proves"(argues) it by saying the ring goes faster some times.
Log in to reply
Yes, I agree that for this problem it is not suitable to go in the frame of center of the wheel as it is non inertial frame.
If rotational speed remains the same wouldn't the nail add to the diameter of the tire at the point at which it is touching the ground and therefore decrease the speed with which the tire itself moves down the road?
The nail would add friction to the tire when the nail is at the bottom which will slow the tire.
The tire, which has uniform distribution of mass, has an added mass of the nail at one particular point. When this mass is at the top, the motion of the tire works to bring the mass down. This is aided by the work of gravity on the added mass of the nail on the otherwise uniform mass of the tire, speeding the motion up. Similarly, when the mass of the nail is at the bottom, the tire has to do work to bring the mass to the top, hindered by gravity on the mass of the nail, slowing this motion down.
As an engineer I can't stand questions like this. In the real world, a nail, even a large one, has negligible mass compared to a tire. The effects of rolling resistance would be far more significant than the tiny changes in speed caused by the changing potential energy of the nail.
Log in to reply
Adam, don't think of it as a normal car tire and an average nail. Think of it as a test toy plastic cylinder and a lead/iron weight. You can imagine the weight on the inside or the side of the tire/cylinder so it doesn't affect the traction.
Log in to reply
I’m with Adam, I have yet to see a real world tire without a rim that is balanced. How much mass does the nail have compared to the tire. Not enough info to answer this with certainty. Yes engineers hate stuff like this
Log in to reply
@Mike Otto – I'm with Adam and Mike....the problem doesn't specify weight/materials/mass/density. The answer given is arbitrary.
Log in to reply
@John Barry Robinson – You guys are overthinking this. This is a simplified math/physics question for highschool. It's not a detailed model for engineers. You are right that certain assumptions should have been specified in the question though. Like assuming that the tire is perfect and light, that the nail was heavy by comparison and it didn't affect the tire by making it bounce.
Log in to reply
@Komninos Maraslidis – If a bunch of unrealistic assumptions are necessary to arrive at the correct solution then those assumptions need to be clearly stated. The problem as stated leaves the reader to use his judgment on what are reasonable assumptions about the problem. In this case two important and unrealistic assumptions about this physical scenario are that rolling resistance is negligible and the mass of the nail isn't negligible.
Log in to reply
@Adam Lohonyai – I was distracted in trying to answer this because I thought some air might be escaping causes a force, Trev
I agree with you Adam, the nail as presented in this problem has negligible effect on the whole system. All else are assumptions.
I'm a retired engineer, I agree it's a BS question. Depending on how I select a frame of reference I can make any of those answers correct.
Log in to reply
Can you elaborate on that? It doesn't sound that convincing. It seems pretty stilted to pick a rotating reference frame.
this is smart
Too many material differences between nail mass/density and tyre compound mass/density - what if the lighter nail displaces heavier compound mass?
"The tire moves faster when the nail is at the bottom" in my opinion is a false statement. I agree that "The tire moves fastest when the nail is at the bottom". As per explanation, At top tyre will start moving faster and at the bottom would be at fastest speed. As soon as the nail is bottom tyre will move slower and slowest at the top.
I think most people who picked Faster at the top has the right idea... but just didn't think it all the way through.
Intuitively, the tire will gain speed as the nail go from high to low. But when will it stop gaining this increased speed??
The answer is when the nail is no longer going from high to low, i.e. when the nail is at the bottom.
In other words, the tire starts gaining speed when the nail goes from high to low. And it finishes gaining all the speed that it gain when the nail hits the bottom, therefore tire is going the fastest when nail is at the bottom.
The nail is actually standing still when it is at the bottom and touching the road and it has near 0 kinetic energy. Since at the bottom point the nail has the least kinetic energy and the least potential energy, the rest of the tire (conservation of energy) has the most kinetic energy (in its cycle) and the tire has no differences in potential energy during the cycle. Ergo the tire moves fastest then.
Another way to think about it is that while the "heavy" nail is rising the tire is decelerating and while it is falling the tire is accelerating. So obviously the fastest tire rotation happens when the nail is at the bottom.
Relevant wiki: Calculating kinetic energy of an object
The top of a wheel travels twice as fast as the centre, and the point in contact with the ground is momentarily stationary.
If we consider the motion of the nail it alternates between having high kinetic energy at the top and none at the bottom. So both the potential and kinetic energy of the nail are at a maximum at the top of the wheel and almost zero at the bottom.
In order for the overall system of wheel and nail to conserve momentum and energy the wheel must speed up when the nail is at the bottom.
The relative magnitude of the kinetic energy and potential energy depends greatly on speed but assuming a wheel diameter of half a meter they would be the same when the top of the wheel is moving at about 3 meters per second, corresponding to the tyre rolling at about 5.5 km per hour.
If the tire speeds up and then slow down, how is the momentum conserved?
Log in to reply
The tyre is not symmetrical and is not all moving horizontally at the same speed. As the nail speeds up (at the top) and slows down at the bottom its momentum goes up and down. For overall momentum to remain the same the tyre’s speed must change. Instead of a nail in a tyre, imagine a large lump of lead on a bicycle wheel.
Log in to reply
Are you saying that the momentum of the tire plus the nail is conserved at all time instants?
Log in to reply
@Rohit Gupta – Yes, that’s my interpretation — energy too, but more complex because of the rotation.
Log in to reply
@Robert Williams – What about friction? Won't friction act to change the momentum of the tire plus nail system?
Log in to reply
@Rohit Gupta – Usually in these sort of problems, friction is ignored unless mentioned. And rolling friction is usually pretty small anyway. They only mention friction so that the tire rolls instead of sliding (like it would on a 0 friction surface, it would not rotate on its own). The tiny amounts of rolling friction (and maybe air resistance friction) do not significantly change this problem anyway. This problem is assuming several facts that have many other people complaining because it is a math problem and not an engineering precise model.
I'm amazed that I was the first upvote on your correct answer while an incorrect one has 53 upvotes, maybe simply because it has a picture attached.
Noooo
Its so simple!!!!
The normal reaction is impulsive in the duration just before the nail hits the ground and just after the nail leaves the ground!!!!!!!
So the change in total momentum is sudden; as a result of which the speed rises more in bottom than while it is at top
As we know that the nail should be more denser than the same amount of time it will increase the velocity of the tire more when it is aided by the force of gravity to roll the wheel in the particular direction so when down it has already helped a lot to increase the rolling speed of the tire therefore when the nail is at the bottom it will have the maximum rolling speed.
Why is there a lack of information regarding the nature of the roll? This answer is only correct if the tire is not rolled on a surface, rather suspended on an axle. If you roll the tire down a street with a nail sticking out of it, the speed reduces when the nail hits the road. Poor question.
Tire goes faster with nail at bottom. But that assumes the density of the nail is greater than density of tire
When the nail is at the bottom, the radius of the tire grows a bit (normal radius + nail). In a circular movement, bigger radius gives a faster linear velocity.
Can't Agree...the correct answer has to be A. The question is when does the tyre rotate "faster" not "fastest". Fastest would be when the Nail is at the bottom but the tyre only starts to rotate "faster" when the Nail is at the top position.
As the nail is at the top(assuming it has mass) it is attracted by the earth by a force(neglecting the fact it isn’t but it’s just a curvature of space-time, but for this purpose this is certainly neglegeable), when the nail is at the top, its potential energy is maximum and the kinetic energy is minimum, while at the bottom he potential energy is minimum and the kinetic energy is maximum, because all the potential energy gets converted into kinetic energy, thereby making the wheel spin faster. Hope that clears it up
The tire plus nail system has the most potential energy when the nail is at the top (due to gravity.)
When the nail comes down, the system starts gaining more and more kinetic energy. The potential energy transfers into kinetic energy.
The system reaches maximum kinetic energy when the nail is at the bottom.
The velocity is higher when the nail is at the bottom because there is more kinetic energy.