Rolls When Completely In!

Electricity and Magnetism Level 5

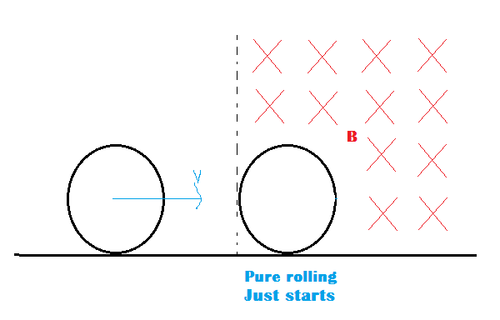
A ring of mass m and radius r and made of an insulating material carries uniform charge. Initially it rests vertically on a frictionless horizontal tabletop on the left side of the vertical plane AA'. In the region to the right side of AA' is a uniform horizontal magnetic field of induction B pointing everywhere parallel to the axis of the ring. The ring is pushed forward with velocity v but no rotation. If $q$ is the charge on the ring so that it just starts rolling on the tabletop on entering completely into the magnetic field, what is [200q] in SI units?

details and Assumptions

$\bullet$ In the given figure cross sign indicates that the field is towards us.

$\bullet$ neglect induced electric fields.

$\bullet$ the mass per unit length $\lambda$

$\bullet$ $\lambda=7$

$\bullet$ $v=3m/s$

$\bullet$ $B=4T$

The answer is 9330.

2 solutions

Milun Moghe
Mar 31, 2014

Let us consider a moment when the cm of the ring travels a distance x. Applying torque equation

$\tau=\int_{-\theta}^{\theta}B(vcos\theta)\lambda(Rd\theta)R=mR^{2}\frac{d\omega}{dt}$

$\frac{2Bv\lambda_{q}sin\theta}{m}=\frac{d\omega}{dt}$ here v is a variable velocity of cm at a certain instant at distance x Imgur Imgur Applying energy conservation , for initial and when just starts rolling Remember that torque due to rotation is zero because the force all the force is passing through the cm therefore i only considered torque due to translation.

$\frac{1}{2}mv^{2}=\frac{1}{2}mv_{f}^{2}+\frac{1}{2}mR^{2}\omega^{2}$

$v_{f}=\omega R$

$\int_{0}^{2R}\frac{2B}{\lambda_{q}}\frac{\sqrt{2Rx-x^{2}}}{R}dx=\int_{0}^{\frac{V}{\sqrt{2}R}}d\omega$

we get $q=\frac{\sqrt{2}mv}{BR}=2\sqrt{2}\pi\frac{\lambda_{m}v}{B}$

$[200q]=9330C$

Lots of mistakes: (Not offensive)

1) You don't consider induced electric field , which is necessary.

2) Even if you don't consider the induced electric field, how can you state that when $v_{f} = \omega R$ , rolling without slipping has started. The net torque and net force both are backwards. When for the first time $v = \omega R$ , the velocity of bottom point is $2v$ .

jatin yadav - 7 years, 2 months ago

Yes, there are many things that the solution is missing.

Anish Puthuraya - 7 years, 2 months ago

Thanks for pounting out Sorry the magetic field direction must be towards us is out of the plane.

Milun Moghe - 7 years, 2 months ago

i was trying using the induced electric field,but the answer came out to be different from the given answer. I don't see a reason why induced field was not taken into account in this solution.

ayush agarwal - 4 years, 8 months ago

too easy,,, but the magnetic field should be at us now away,, unless the charge given is negative,,, But u solved in too complex manner,. heres how you should do it,, see when it completely enters magnetic field,.,. each point on the ring rotates at v and translates at v (pure rolling) thus net velocity is root 2 * v ,, now use the formula qvB= mv^2/r and substitute v root 2 for v and put values,, then get q multiply by 200 u will get 9330.05 then take greatest integer function to get 9330

Mvs Saketh - 7 years, 1 month ago

can u explain torque equation

Dhruv Aggarwal - 5 years, 1 month ago

But, when the ring has traveled a distance $x$ , wouldn't it be rotating as well? So, why didn't you consider the Force due the rotational interaction with the magnetic field?

To make it clear, let the angular velocity of the ring at a distance $x$ be $w$ .

Taking the element at $\theta$ with an angular width of $d\theta$ , the Lorentz force due to this $w$ will be,

$\displaystyle dF = B(wR)(\lambda R d\theta)$ (Note that $dF$ acts towards the center of the ring)'

As $dF$ acts towards the center of the ring, it won't produce a torque, but surely the summation of $dF\cos\theta$ (vertical component of $dF$ cancels out due to symmetry) would result in a net force, acting opposite to the motion of the ring (towards left).

So, why didn't you consider the work done due to this force?

Anish Puthuraya - 7 years, 2 months ago

The net work done by magnetic field is $0$ . Divide the ring in elements, and on each element, force is perpendicular to velocity. Hence, it does no work on any element and hence on the ring.

jatin yadav - 7 years, 2 months ago

I agree with you work done due to magnetic force ie passing through the cm Is zero torque is also zero. The only mistake is that I didn't mention to neglect induced electric field and also I made a silly mistake while mentioning the direction of magnetic field. I have made corrections. Thank you for the clarification.

Milun Moghe - 7 years, 2 months ago

@Milun Moghe – Torque of magnetic field due to rotation is $0$ , not due to translation. Net torque due to magnetic field is not 0. You too know that as you used it in solution :P

jatin yadav - 7 years, 2 months ago

@Jatin Yadav – yes i mean due to rotation torque as well as work is zero

Milun Moghe - 7 years, 2 months ago

Well considered torque about cm so due to the angular velocity the force will pass through the cm

Milun Moghe - 7 years, 2 months ago

Mayank Singh
Jun 29, 2015

Hats off to the question maker

Rolls When Completely In!

The answer is 9330.

2 solutions

0 pending reports