Rhombus Grid
To go from A to B , you only can move along ↗ and ↘ and you can't pass through more than one star.
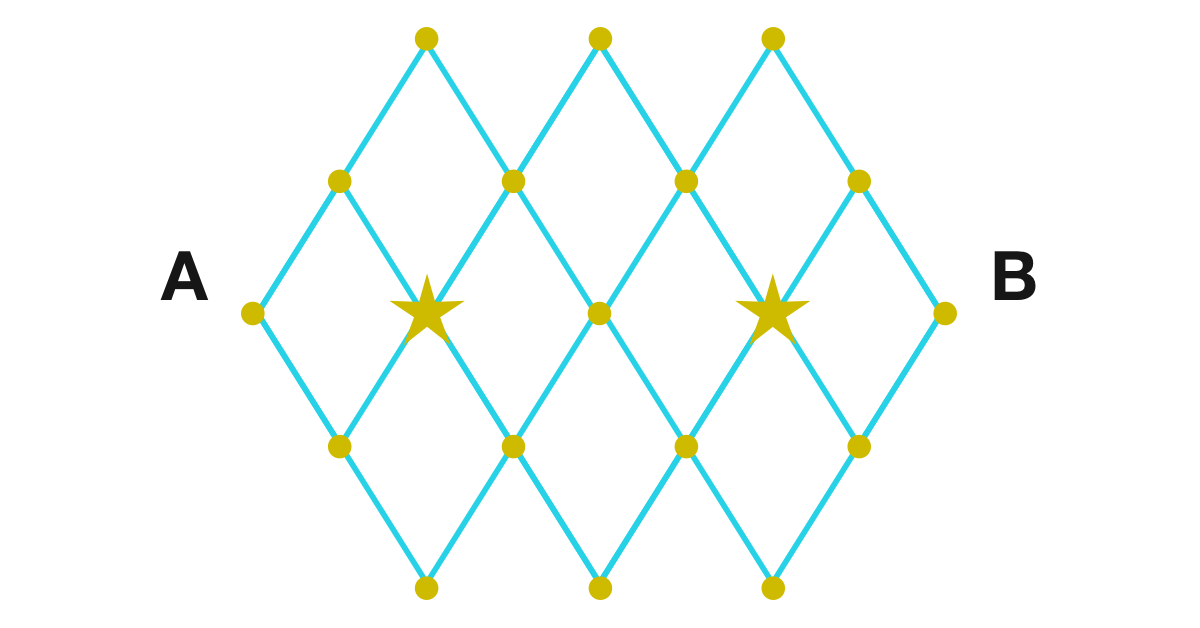
How many paths are there to go from A to B ?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks. I've updated the answer from 36 to 30. Those who previously answered 30 will be marked correct, while those who previously answered 36 will be marked wrong.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “line line line” menu in the top right corner. This will notify the problem creator who can fix the issues.
Just a matter of waiting out rounds in the roster. If you count them with passing through the first star, you May double your answer because of the symmetry. So op the outside you got 1's. Gettin to the star makes 2, from the star to outside makes 3 routes above and 3 routes down. You got 6 routes to middle. Since you can't pass trough the 2nd star, there are 9 rounds around via the top and 9 via the downside. Hence 18 routes from A to B through the first star. This makes 36 routes in total.
By mirroring the 18, you are counting 6 paths twice. The 6 paths that don't go through any of the stars.
Log in to reply
So it would make 35 routes then? Or am I counting one path twice and am i forgetting another route?
Log in to reply
Nope, 30. From A to B there are 6 paths that do not pass through any star, and you are counting these paths twice!
Log in to reply
@Romain Farthoat – Hmmm it Does give me a correct when i answer 36, so i am gonna rethink :) And rethinking helped: Just took al the paths from A to B and took out those that passed through both the stars: 54 - 2 x 6 x 2 = 30
I drew a first grid that passed through the first star, with A paths, a second grid that passed through the second star with B paths then I drew a grid that didn't pass trough any star with A ∩ B paths. By using Pascal's Triangle, I calculated : ( A ) + ( B ) − ( A ∩ B ) ↔ 1 8 + 1 8 − 6 = 3 0 I don't know why this is level 5 honestly. The strange thing is that the answer 30 was not accepted.
Log in to reply
That is why i didnt see my double count
It is definitely 30 paths.
Relevant wiki: Rectangular Grid Walk
We can obtain the number of paths easily by using this method:
Give every dot a value of 0 .
Add 1 to A :s value.
Add A :s value to the dots to which can be moved from A .
Repeat the last step for every new dot you add to until you get to B .
The number of paths is the value of B .
Let's divide the problems into 3 separate cases.
Case 1: Passing trough no stars
Imagine that the dots with a star don't exist and calculate the number of possible paths which is 6 .
Case 2: Passing trough the first star
Imagine that the dots above and below the first star don't exist (forcing the path go through the first star) and calculate the number of possible paths which is 1 2 .
Case 3: Passing trough the last star
By symmetry the number of paths is also 1 2 .
Adding the values we obtain the answer: 6 + 1 2 + 1 2 = 3 0 .
You could also calculate the number of all paths and then subtract the number of paths which go through both stars. This also gives the same answer