Roots Dilemma
Let a , b and c be the three roots of x 3 − x + 1 = 0 . Find the value of a + 1 1 + b + 1 1 + c + 1 1 .
The answer is -2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Your last equation states that, a 2 + b 2 + c 2 = − 2 .
How is sum of 3 squares equal to -2?
Log in to reply
But it is true that a 2 + b 2 + c 2 = 2 actually and not -2; there is an error in the solution: a b + b c + a c is not actually 1 but -1
a, b and c are complex numbers not all are real or none is real.
It states that a^2 +b^2 +c^2 = 2 not -2
Log in to reply
It was -2 at first. It's corrected now. So, all well and good. :D
Log in to reply
@A Former Brilliant Member – But in other problems, sum of squares can be negative because of complex numbers. For example if a , b and c are roots of x 3 + x + 1 = 0 . Then a + b + c = 0 , a b + b c + c a = 1 and a 2 + b 2 + c 2 = ( a + b + c ) 2 − 2 ( a b + b c + c a ) = 0 2 − 2 ( 1 ) = − 2 . This is because the roots of x 3 + x + 1 = 0 are a = − 0 . 6 8 2 3 3 , b = 0 . 3 4 1 1 6 − 1 . 1 6 1 5 4 i , and c = 0 . 3 4 1 1 6 + 1 . 1 6 1 5 4 i . You will note that a + b + c = 0 and a 2 + b 2 + c 2 = − 2 .
Log in to reply
@Chew-Seong Cheong – Here real values deal only :)
@Chew-Seong Cheong – I know sir, but I just corrected since it wasn't negative in this question.
Because all the roots need not be real.
Log in to reply
But in this case the sum of squares is positive by the use of formula, that's why I suggested. I understand that it can be negative at times due to complex numbers.
How did you make the jump from the polynomial with y to the final solution?
Log in to reply
y = 1/(x+1)
the roots of the polynomial with y are 1/(a+1), 1/(b+1), 1/(c+1).
Perfect! Same method!
Same method by me 2
perfect! did the same
Observe that: x 3 − x + 1 = ( x − a ) ( x − b ) ( x − c ) = x 3 − ( a + b + c ) x 2 + ( a b + b c + c a ) x − a b c .Therefore a + b + c = 0 , a b + b c + c a = − 1 ... (1)
And: When x = − 1 , 1 = ( − 1 ) 3 − ( − 1 ) + 1 = ( − 1 − a ) ( − 1 − b ) ( − 1 − c ) = − ( 1 + a ) ( 1 + b ) ( 1 + c ) ... (2)
a + 1 1 + b + 1 1 + c + 1 1 = ( 1 + a ) ( 1 + b ) ( 1 + c ) a b + b c + c a + 2 ( a + b + c ) + 3
By substituting (1) and (2), = − 1 − 1 + 2 ( 0 ) + 3 = − 2
if a,b,c are roots, then f ( x ) = x 3 − x + 1 = ( x − a ) ( x − b ) ( x − c ) d.w.r.x f ′ ( x ) = 3 x 2 − 1 = ( x − a ) ( x − b ) + ( x − b ) ( x − c ) + ( x − c ) ( x − a ) divide: f ( x ) f ′ ( x ) = x 3 − x + 1 3 x 2 − 1 = ( x − a ) ( x − b ) ( x − c ) ( x − a ) ( x − b ) + ( x − b ) ( x − c ) + ( x − c ) ( x − a ) = x − a 1 + x − b 1 + x − c 1 x = -1: 2 = − ( 1 + a 1 + 1 + b 1 + 1 + c 1 ) hence answer is − 2
Let y = x + 1 .
( y − 1 ) 3 − ( y − 1 ) + 1 = 0
y 3 − 1 − 3 y ( y − 1 ) − y + 2 = 0
y 3 − 3 y 2 + 2 y + 1 = 0
Let z= y 1
y = z 1
z 3 1 − z 2 3 + z 2 + 1 = 0
z 3 + 2 z 2 − 3 z + 1 = 0
Roots of this equation are a + 1 1 , b + 1 1 , c + 1 1
Sum of roots =-2.
Expanding numerator and denominator by simply taking LCM and multiplying we get [2(a+b+c) + (ab+ bc +ca)+3]
divided by
[(abc)+(ab+bc+ca)+(a+b+c)+1]
.....(1)
Now from the cubic equation of general form
Px^3+Qx^2+Rx+S
having roots a,b,c we know Sum of roots =a+b+c= -b/a
Sum of product of root taken two at a time =ab+ bc +ca =c/a
Product of roots = abc = -d/a
Comparing this with
x^3-x+1 we get
a+b+c = 0
ab+ bc +ca=-1
abc=-1
Now substituting in (1) we get ans as -2
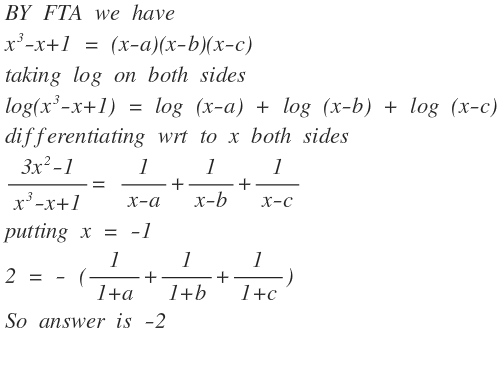

FTA means Fundamental Theorem of Algebra :- https://brilliant.org/wiki/fundamental-theorem-of-algebra/
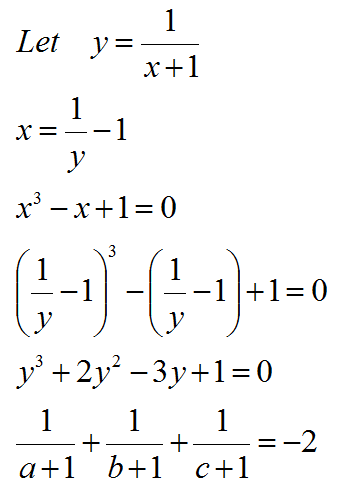
Since x 3 − x + 1 = 0 ⇒ 1 = x − x 3 = x ( 1 − x 2 ) = x ( 1 − x ) ( 1 + x ) . Therefore,
a + 1 1 + b + 1 1 + c + 1 1 = a + 1 a ( 1 − a ) ( 1 + a ) + b + 1 b ( 1 − b ) ( 1 + b ) + c + 1 c ( 1 − c ) ( 1 + c ) = a ( 1 − a ) + b ( 1 − b ) + c ( 1 − c ) = a + b + c − ( a 2 + b 2 + c 2 ) See Note. = 0 − ( 2 ) = − 2
Note: Using Vieta's formulas, we have:
a + b + c = 0
a 2 + b 2 + c 2 = ( a + b + c ) 2 − 2 ( a b + b c + c a ) = 0 2 − 2 ( − 1 ) = 2