Rope between inclines?
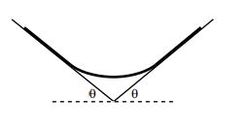 A rope rests on two platforms which are both inclined at an angle
θ
(which you are
free to pick), as shown. The rope has uniform mass density, and its coefficient of
friction with the platforms is 1. The system has left-right symmetry.
A rope rests on two platforms which are both inclined at an angle
θ
(which you are
free to pick), as shown. The rope has uniform mass density, and its coefficient of
friction with the platforms is 1. The system has left-right symmetry.
What is the largest possible fraction of the rope that does not touch the platforms?
What angle θ allows this maximum value?
Enter your answer as the sum of the answers of these questions.
Please take θ in degrees.
The answer is 22.672.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Please add that theta is an angle in degrees. I used radians.
Log in to reply
Thanks I have updated the question.
Then why don't you up vote my solution?
Log in to reply
Because It's not yours.... http://liquids.seas.harvard.edu/oleg/competition/BAUPC_sols04.pdf
Let α be the fraction of the rope that is suspended in the air. It follows that 1 − α is the fraction of the rope that is touching the side of the inclined plane. It must be true that the gravitational force acting on the fraction the rope suspended between the two surfaces must be in balance with the force acting upwards on this component of the rope, which will be the tension at the point that the rope leaves the surface on either side of the suspended rope, which we call T 0 . Thus, we have:
2 T 0 sin θ = α L λ g
Where L is the length of the rope and λ is the mass density. Now, let's turn our attention away from the suspended component of the rope, and consider the components of the rope that are touching the surfaces. These components of the rope must also be in equilibrium. Thus, we have (on either side):
2 1 ( 1 − α ) L λ g [ − sin θ + cos θ μ k ] = T 0
Thus, we will have:
[ − sin θ + cos θ μ k ] sin θ = 1 − α α
And we then re-arrange, getting α ( θ ) :
α ( θ ) = [ − sin θ + cos θ μ k ] sin θ + 1 [ − sin θ + cos θ μ k ] sin θ = [ − sin θ + cos θ μ k ] sin θ + 1 [ − sin θ + cos θ μ k ] sin θ
We then take the derivative with respect to θ and find the value of (\theta) that corresponds to maximum α in the range 0 to 2 π , which turns out to be 8 π , which is equivalent to 2 2 . 5 degrees. Finally, we can plug this back into the original equation, getting α Max = 0 . 1 7 2 .
Adding these results together, we get 2 2 . 5 + 0 . 1 7 2 = 2 2 . 6 7 2
By the way, you could have just considered the vertical force acting on the whole system, but I think it is slightly cleaner considering the two sub-systems of the rope!
Therefore the answer is 22.5 + 0.172 , which is equal to 22.672.