Rope Sliding on Double Ramp
A 1 k g rope of length 1 . 5 m slides down a frictionless double ramp in the shape of an equilateral triangle, as shown in the diagram above. At time t = 0 , the rope is at rest with 1 m of its length on the right side of the ramp.
How much time (in seconds, to 3 decimal places) elapses before all of the rope is on the right side?
Details and Assumptions:
- The downward gravitational acceleration is 1 0 m / s 2 .
The answer is 0.519.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Why do we subtract the two forces when they aren't opposite to each other?
Log in to reply
The force of the portion of the rope on the left side effectively acts at the apex of the ramp, and thus are in effect opposite to one another.
Log in to reply
I am not able to follow you. Isn't the gravitation force acts at the center of the rope as it is uniform? Why does the force act at the apex? Or, can we find the force that the apex apply on the rope?
Log in to reply
@Rohit Gupta – Suppose for a moment we cut the rope at the apex and hold on to the portion on the left side at the apex. The force we would feel would then be x 1 . 5 − x g cos ( 3 0 ∘ ) . This is the force that would be restraining the portion of the rope on the right side from sliding down the ramp.
Let the length of the rope be L , and L 1 , L 2 the length of rope on either side. Define u such that L 1 , L 2 = 2 L ± u . The advantage of this definition is its symmetry: at u = 0 the rope is in (unstable) equilibrium. Note that for the given values, L = 1 . 5 and the initial and final values of u are u 0 = L / 6 , u f = L / 2 .
Let μ be the linear mass density of the rope. I don't expect it to matter for the answer; it will cancel out in the calculations.
We determine the potential energy of each part of the rope relative to the top of the triangle. We multiply its mass μ L i by g and by the vertical distance of its center of mass below the top, which is − 2 1 c L . Here, c describes the geometry of the ramp: c = cos 3 0 ∘ = 2 1 3 . Thus U 1 , U 2 = m g h = μ L i g ( − 2 1 c L i ) = − 2 1 μ c g L i 2 . Expressing the L i in our variable u we find for the total potential energy U = U 1 + U 2 = 2 1 μ c g ( ( 2 L + u ) 2 + ( 2 L − u ) 2 ) 2 1 μ c g ( 2 u 2 + ⋯ ) = μ c g u 2 . The expression on the dots does not depend on u . We can ignore it, because that simply means choosing a new zero for potential energy.
Conservation of energy tells us that the kinetic energy during any moment of the motion is K = U 0 − U = μ c g ( u 2 − u 0 2 ) . Using K = 2 1 m v 2 = 2 1 μ L v 2 we find v = L 2 c g u 2 − u 0 2 . The rate of change of u is equal to the speed of each part of the rope. Therefore we can write for any infinitesimal movement of the rope d t = v d u . Integrate this: t = ∫ u 0 u f d t = ∫ u 0 u f v d u = 2 c g L ∫ u 0 u f u 2 − u 0 2 d u = 2 c g L ( ln ( u + u 2 − u 0 2 ) − ln u 0 ) = 2 c g L ln ⎝ ⎛ u 0 u + ( u 0 u ) 2 − 1 ⎠ ⎞ . In the given situation, u / u 0 = 3 ; L = 1 . 5 ; g = 1 0 ; and c = 2 1 3 . Thus t = 1 0 3 1 . 5 ln ( 3 + 8 ) ≈ 0 . 5 1 8 7 4 7 .
Consider a small section near the corner. Its velocity changes its direction as it moves from the left side to the right side. This change in the velocity occurs in split second for this portion. Thus, this portion must feel a jerk somewhat like a collision. Why will the energy remains conserved in such a case?
Log in to reply
The forces by the triangle on the rope are perpendicular to the rope at any point, and therefore do no work. If there were a parallel component of force, it would no longer be frictionless.
Log in to reply
Ok, I have one more question for you to explain my point in this case.
https://brilliant.org/problems/blending-of-mechanics-and-calculus/
(Please read the solution discussion as well.) Will there be a loss in energy? I mean will the work done by the person pulling the rope be equal to the increase in the mechanical energy of the rope? If there is a loss in the energy, then why and why not in this case?
Log in to reply
@Rohit Gupta – I read that problem and solved it. With conservation of energy you'll end up with a slightly smaller answer than be analyzing the forces/impulses involved. The reason is that in this situation some of the work is transferred to the rope that is still on the ground, where is apparently is dissipated. Or, viewing it a different way, when a piece of rope is suddenly put into motion, it should vibrate if it were elastic; it doesn't because apparently friction takes away any relative motion within the rope.
In any case, none of this plays a role in the current problem. If the ramp is free of friction, then by definition all forces between ramp and rope are perpendicular to the motion, and thus do not do any work.
Log in to reply
@Arjen Vreugdenhil – This is exactly my point, whenever a portion of the rope which is at rest suddenly put into motion, some energy is lost due to inelastic nature of the rope. In other words, if a portion of the rope gets an impulsive acceleration then some energy is lost.
Now, in the current situation, the portion that crosses the apex will suddenly feel an impulsive acceleration and some energy should be lost. Thus, we should not conserve the energy here.
Log in to reply
@Rohit Gupta – In this case the acceleration is perpendicular to the motion. Therefore it does no work, and energy can be conserved. This is borne out by the fact that Brian, who does a force analysis, finds the same answer as I with my energy analysis.
Log in to reply
@Arjen Vreugdenhil – Are you sure the acceleration is perpendicular to the motion? I think it is along the rope.
Log in to reply
@Rohit Gupta – I should have been clearer. Instead of "acceleration" I meant "force by the ramp". The acceleration of the rope is parallel to the rope at all points.
The diagram below is an analysis of the forces at three points along the rope. Black = gravity, green = tension, red = normal force. The force of gravity does work but is conservative; the tension force does not do work because the rope does not change length; the normal force does not do work because it is perpendicular to the movement.
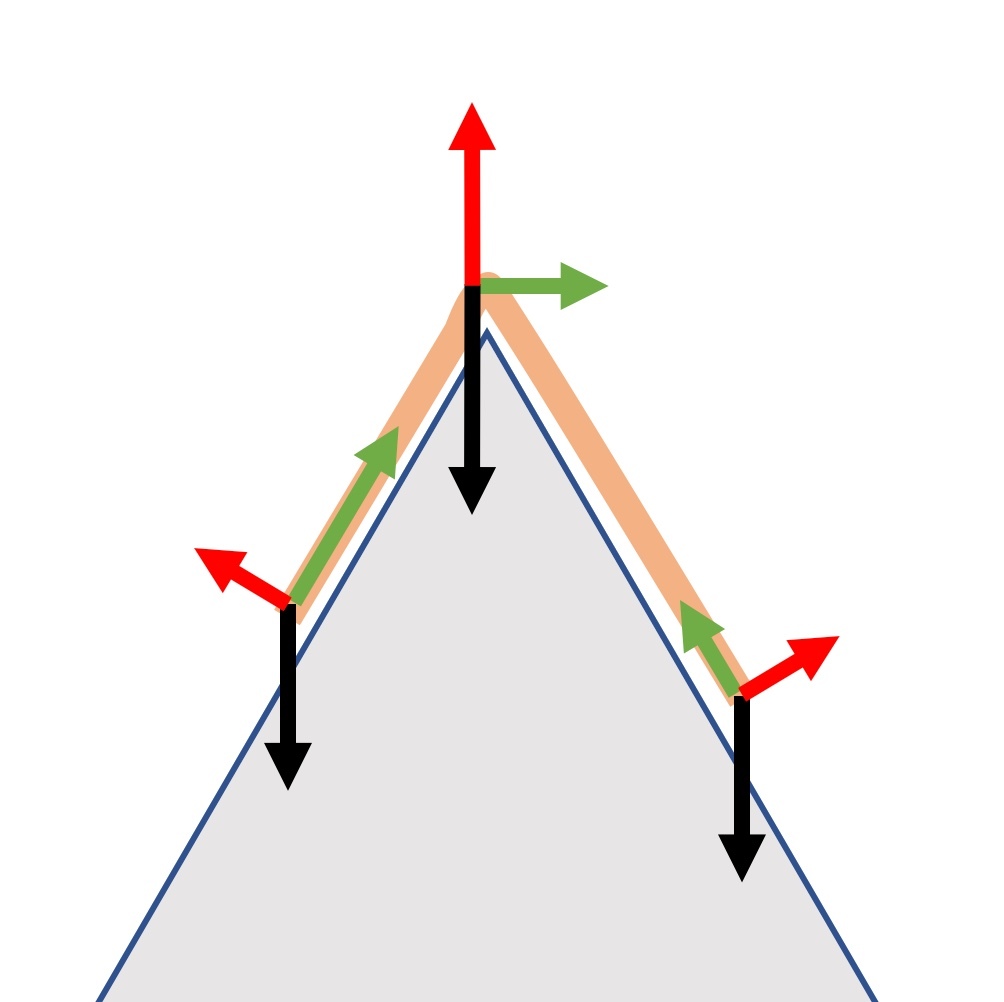
Log in to reply
@Arjen Vreugdenhil – What about the direction of acceleration of the point of the rope that is crossing the apex of the ramp? Will it have an acceleration along the rope or vertically downwards? I think it should be vertically downwards considering the velocity of it just before and after crossing the apex.
Log in to reply
@Rohit Gupta – That is correct. Still, that acceleration is perpendicular to the velocity of the rope at that point, which is horizontal.
Log in to reply
@Arjen Vreugdenhil – Ahh, yes. Where the acceleration is finite and non-impulsive there the acceleration is along the rope, but at the apex where the acceleration is impulsive, it is perpendicular to the rope. Whereas in the lifting the rope problem, the acceleration is impulsive and still along the rope and results in its stretching and loss of energy. Thanks!
This solution was a little bit off because I do not know a lot of physics formulas, but this is what I did. Let's assume that the rope has an equal mass distribution throughout. We see that the acceleration down the slope on both sides of the triangle is cos ( 3 0 ) 1 0 = 3 2 0 = 3 2 0 ⋅ 3 s 2 m Using the force equation F = m ⋅ a , we see that the force on the right side is F r i g h t = 3 2 0 ⋅ 3 s 2 m ⋅ 3 2 k g = 9 4 0 ⋅ 3 N and the force on the left side is F l e f t = 3 2 0 ⋅ 3 s 2 m ⋅ 3 1 k g = 9 2 0 ⋅ 3 N Since the force on the left side is opposing the force on the right side, we subtract the force on the left side from the force on the right side. F r i g h t − F l e f t = 9 4 0 ⋅ 3 − 9 2 0 ⋅ 3 = 9 2 0 ⋅ 3 N Converting this back to an acceleration constant, we see the acceleration of the entire rope towards the right side is 9 2 0 ⋅ 3 s 2 m In order to find the time it takes for the rope to move all the way to the right side, we take the integral of this to find the velocity in respect to time. ∫ 9 2 0 ⋅ 3 d t = 9 2 0 t ⋅ 3 s m Now we want to find when the distance traveled is 0 . 5 meters Therefore, we find the value x such that ∫ 0 x 9 2 0 t ⋅ 3 d t = 0 . 5 ∫ 0 x 9 2 0 t ⋅ 3 d t = 0 . 5 9 1 0 x 2 ⋅ 3 − 9 1 0 ⋅ 0 2 ⋅ 3 = 0 . 5 9 1 0 x 2 ⋅ 3 = 0 . 5 1 0 x 2 ⋅ 3 = 4 . 5 x 2 = 2 0 3 ⋅ 3 x = 2 0 3 ⋅ 3 ≈ 0 . 5 1 0 The actual answer was 0 . 5 1 9 . If someone can explain to me what I did wrong, that would be great.
you have assumed that atall times it has constant acceleration , whereas accelration in this case vill vary with x, hence the difference
Log in to reply
Yes, you calculated the initial acceleration and assumed that constant throughout the motion. Whereas, as the rope slides more towards one side its acceleration will increase.
Consider at time t when the rope has slid a length of x on the right side. The force on the rope is due to the weight on the right side minus that on the left side, that is:
F m x ¨ x ¨ 3 x ¨ x ( t ) x ˙ ( t ) x ( t ) = λ ( 1 + x − ( 0 . 5 − x ) ) g cos 3 0 ∘ = 3 2 ( 2 1 + 2 x ) ⋅ 1 0 ⋅ 2 3 = 3 5 ( 1 + 4 x ) = 2 0 x + 5 = c 1 e 4 3 2 5 t + c 2 e − 4 3 2 5 t − 4 1 = 4 3 2 5 ( c 1 e 4 3 2 5 t − c 2 e − 4 3 2 5 t ) = 8 1 ( c 1 e 4 3 2 5 t − c 2 e − 4 3 2 5 t ) − 4 1 = 4 1 cosh ( 4 3 2 5 t ) − 4 1 where λ is the unit mass of the rope. where m and x ¨ are the mass and acceration of the rope. Solving the 2nd order linear ODE. Putting t = 0 ⟹ c 1 + c 2 = 4 1 As velocity x ˙ ( 0 ) = 0 ⟹ c 1 = c 2 = 8 1
When all the rope is just on the right side, x = 2 1 , then:
4 1 cosh ( 4 3 2 5 t ) − 4 1 cosh ( 4 3 2 5 t ) 4 3 2 5 t ⟹ t ≈ 0 . 5 1 9 = 2 1 = 3 = ln ( 3 + 2 2 ) = ln ( 3 + 2 2 ) ⋅ 2 5 4 3
What about the force that the apex of the triangular ramp applies on the rope? Are we neglecting it?
Log in to reply
The force comes from the weight of the rope. The force from the apex is a reaction and by Newton's third law, action and reaction are balanced and it does not affect the movement. Only the weight of the rope down the ramp causes the movement.
Log in to reply
It is not correct to say that action and reaction are balanced and do not affect the movement. The reason is that action and reaction are forces on two different objects. The apex of the triangle pushes upward on the rope, and the rope pushes downward of the apex.
The reason why the force of the apex need not be considered is that it acts on an infinitely small part of the rope. By accounting for the normal forces on both sides of the apex (the cosine factor), you accounted for all the force by the ramp on the rope.
Let x be the length of rope (in meters) on the right side of the ramp and 1 . 5 − x be the length of rope on the left side. As the entire rope has mass 1 kg, the mass of the portion of the rope on the right side is 1 . 5 x kg, and on the left side 1 . 5 1 . 5 − x kg.
The force pulling the rope down the right side is then 1 . 5 x g cos ( 3 0 ∘ ) , i.e., the component of the weight of the rope on this side that is in line with the ramp, and the force restraining it is 1 . 5 1 . 5 − x g cos ( 3 0 ∘ ) , the component of the weight of the rope on the left side that is in line with the left side of the ramp. Thus the acceleration of the rope down the right side of the ramp is
a = 1 . 5 x g cos ( 3 0 ∘ ) − 1 . 5 1 . 5 − x g cos ( 3 0 ∘ ) = 1 . 5 2 x − 1 . 5 × 1 0 × 2 3 = 3 5 3 ( 4 x − 3 ) .
Now by the chain rule a = d t d v = d x d v d t d x = v d x d v , so we have that
v d x d v = 3 5 3 ( 4 x − 3 ) ⟹ v d v = 3 5 3 ( 4 x − 3 ) d x ⟹
2 v 2 = 2 4 5 3 ( 4 x − 3 ) 2 + C ⟹ v = d t d x = 1 2 5 3 ( 4 x − 3 ) 2 + C .
Now v = 0 when x = 1 , so we see that C = − 1 2 5 3 , and so
d t d x = K × ( 4 x − 3 ) 2 − 1 where K = 2 1 3 5 .
Separating and integrating, we then have that
∫ ( 4 x − 3 ) 2 − 1 d x = K t + D ⟹ ∫ sec ( θ ) d θ = 4 K t + D ,
where the substitution 4 x − 3 = sec ( θ ) was made. This last integral is standard, so we have
ln ( 4 x − 3 + ( 4 x − 3 ) 2 − 1 ) = 4 K t + D , with the initial condition x ( 0 ) = 1 giving us D = 0 .
Solving for t , we have that t = 2 1 5 3 × ln ( 4 x − 3 + ( 4 x − 3 ) 2 − 1 ) .
Plugging in x = 1 . 5 gives us a desired time of 2 1 5 3 × ln ( 3 + 2 2 ) = 0 . 5 1 9 seconds to 3 decimal places.