Rotate that Cuboid
A cuboid has base dimensions 3 0 × 2 0 and a height of 1 0 and is lying flat on the x y -plane.
It undergoes two rotations—the first is 3 0 ∘ about the edge measuring 2 0 , and the second is also 3 0 ∘ about the edge measuring 3 0 . Both rotations are such that the center of the cuboid is raised upward.
Find the z -coordinate (that is, the altitude) of the highest point of the cuboid after applying the two rotations (to 2 decimal places).
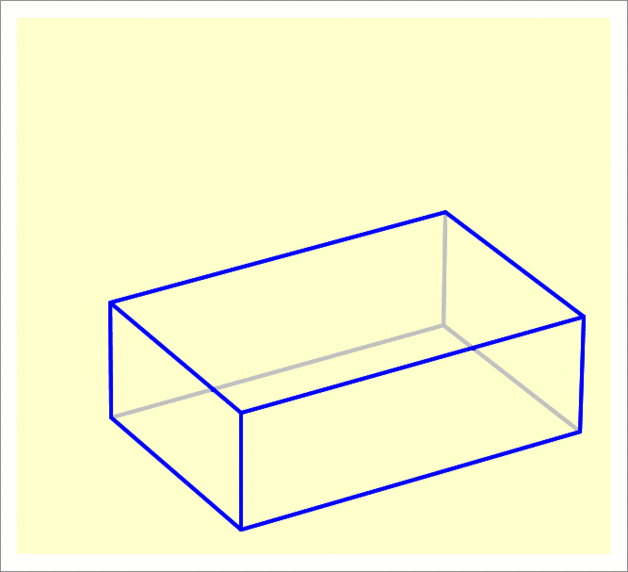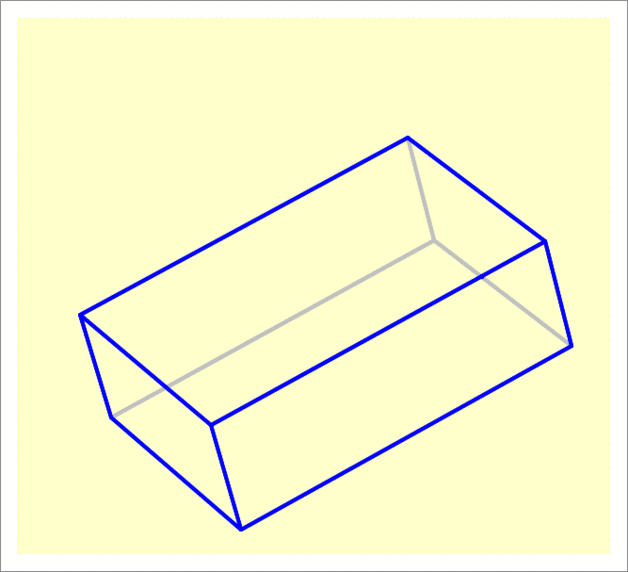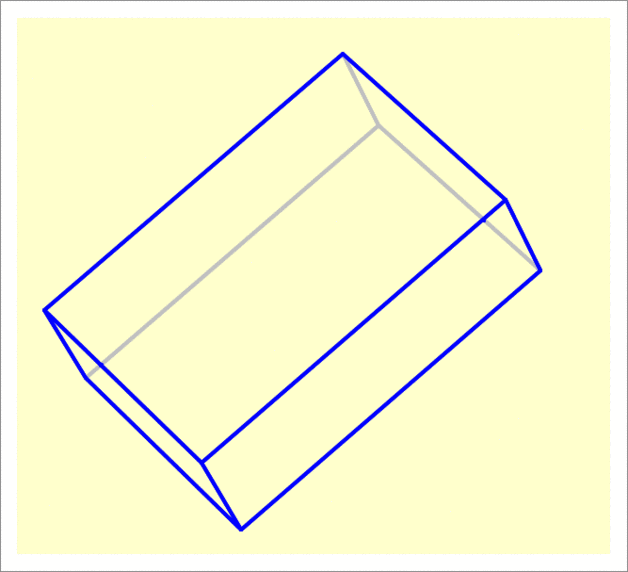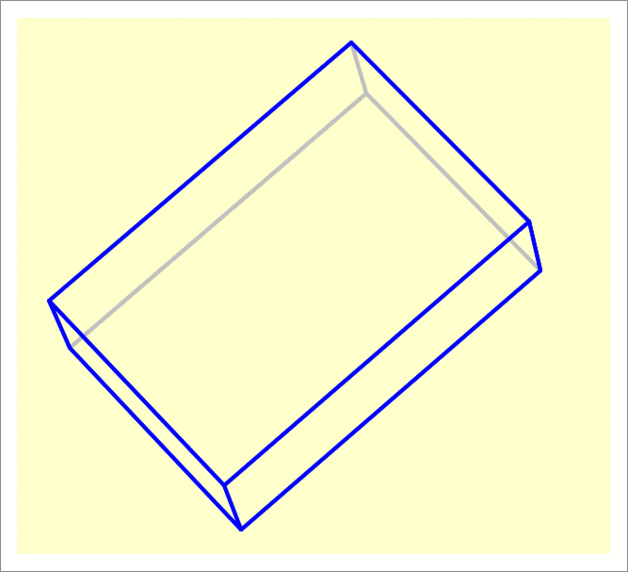
The answer is 31.16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Could you please explain why the first rotation is clockwise?
Log in to reply
If you consider the edge of length 20 to be the y-axis, and the origin is the near vertex to the viewer, then the y-axis is pointing into the page towards the left, therefore, the rotation described in the problem and shown in the GIF animation is clockwise.
According to the problem, you should apply R2xR1and multiply with (30,20,10) and your answer will change from 31.16=(90+20√3)/4, to 30.490 = (35+15√3)/2. Refer to my reply (Vinod Kumar, Jul-24).
Log in to reply
In my solution, it is explained clearly why the overall rotation matrix is R 1 R 2 and not R 2 R 1 . Please read my solution carefully, and if you have further questions, I'll be happy to answer them.
Log in to reply
I didn't understand either. Trying to solve the problem I used R 2 R 1, later running in a program the rotation was an absurd, however even reading your solution I could not understand. Would you explain why is R 1 R 2?
Log in to reply
@Gustavo Exel – Looking back at my solution, we see that there are three coordinate frames , 1. the original frame, 2. the frame after the first rotation, and 3. the frame after both rotations are applied. If the coordinates with respect to these frames are , respectively, p0, p1, p2, then we have
p0 = R1 p1
p1 = R2 p2
hence p0 = R1 R2 p2
That shows why the overall rotation matrix is R1 R2. (Remember again, we are not rotating the solid about the fixed x-axis and y-axis of the original frame. ( frame 1 ) )
Please explain and give explicitly the value of new Z coordinate after applying the first rotation along the Y-axis. Don't apply the second rotation at all.
In the problem, this first rotation is along the edge-20 (Y-axis).
According to your comments this should be given by p1=R2.p2, which is completely incorrect.
After receiving your answer, I will apply the second rotation.
Log in to reply
If you want to apply the two rotations one by one, first then second, the first rotation is straight forward and is a rotation about the y-axis by an angle of (-30) degrees. However the second rotation is a rotation about an axis that is different from the x-axis, so a general rotation matrix needs to be applied (one that accomodates a general orientation axis of rotation).
However, this is not necessary at all. Looking back at my solution, we see that there are three coordinate frames , 1. the original frame, 2. the frame after the first rotation, and 3. the frame after both rotations are applied. If the coordinates with respect to these frames are , respectively, p0, p1, p2, then we have
p0 = R1 p1
p1 = R2 p2
hence p0 = R1 R2 p2
That shows why the overall rotation matrix is R1 R2. (Remember again, we are not rotating the solid about the fixed x-axis and y-axis of the original frame. ( frame 1 ) )
Vinrod: Please note that after the first rotation, the x axis has rotated into the x' axis, and the second rotation is performed with respect to this new axis. Your answer would be correct if the second rotation were performed with respect to the original x axis.
Maybe your explanation is a little bit confusing. But you get to the same matrix R as yours if you rotate the coordinta system twice (instead of rotationg the point). Or in other words you rotate the cuboid with the coordinate system attached to it. Remember, for coordinate transformations you need the inverse matrices. So this would look like following: p1=(R1^-1)p0 p2=(R2^-1)p1=(R2^-1)(R1^-1)p0 And like you said p2 is point with coordinates with respect to the coordinate system attached to the cuboid. So all we have to do now ist to get p0. (R1)(R2)(R2^-1)(R1^-1)p0=(R1)(R2)p2 p0=(R1)(R2)p2
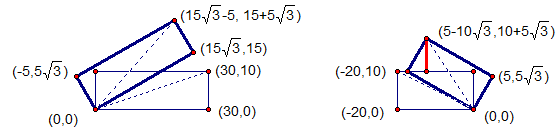
For each rotation, view the axis of rotation straight on and call it ( 0 , 0 ) for convenience. They don't have much to do with 3-d coordinates, but they help visualize the change in height.
The first rotation is shown in the first picture. It shows the height of that back corner becoming 1 5 + 5 3
The second rotation is the tricky one. The back corner doesn't really rise by the height of the red line which is 1 0 + 5 3 − 1 0 = 5 3 because the face of that rectangle is tilted 30 degrees from perpendicular. Instead the increase in height is only cos 6 0 = 2 3 of this.
Total height is then 1 5 + 5 3 + 2 3 ⋅ 5 3 = 2 4 5 + 5 3 ≈ 3 1 . 1 6
Can you explain why you had to multiply specifically by cos 60?
Log in to reply
It was a bit of intuition, I guess, but try this: look at the animation, when it does the second rotation imagine the plane containing the 10x20 in the back. It is no longer perpendicular (90 degrees) to the floor because of the first rotation. Instead, it's only 60 degrees. cos(90)=1, so you would be able to ignore this angle. The flatter the plane gets the less increase you get, though.
Let the lowest corner point of the cube after the two rotations be the origin O ( 0 , 0 , 0 ) of ( x , y , z ) coordinate system, where x -, y -, and z -axes are parallel to the respective edges of the cube before the two rotations. Now let the other corner point sharing the adjacent edge with O be another origin O ′ of ( x ′ , y ′ , z ′ ) coordinate system, where x ′ -, y ′ -, and z ′ -axes are parallel to the respective edges of the cube after the two rotations.
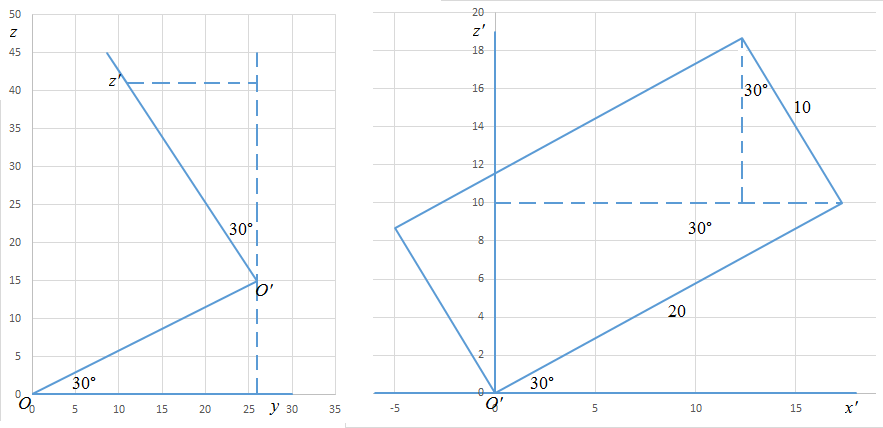
Then we note that z = z ′ cos 3 0 ∘ + 3 0 sin 3 0 ∘ = 2 3 z ′ + 1 5 (see diagram). Since the z ′ of the highest corner point is z ′ = 1 0 cos 3 0 ∘ + 2 0 sin 3 0 ∘ = 5 3 + 1 0 . Therefore, z = 2 3 ( 5 3 + 1 0 ) + 1 5 ≈ 3 1 . 1 6 .
Note: x = x ′ and y = 1 5 3 − 2 y ′ .
"where -x', -y', and -z' axes are parallel to the respective edges of the cube after the FIRST rotation", no ?
Log in to reply
x ′ -, y ′ - and z ′ -axes are always parallel to the respective edges of the cuboid.
Swapping the two rotation steps, that is, rotating the cuboid 3 0 ° along the 3 0 unit edge parallel to the x z -plane and then rotating the result 3 0 ° parallel to the y z -plane, results in the same altitude, but the calculations are easier since the rotations are both on orthogonal planes.
If we first rotate the cuboid at an angle of 3 0 ° along the 3 0 unit edge, two 3 0 ° - 6 0 ° - 9 0 ° triangles are formed with hypotenuses of 1 0 and 2 0 , giving the highest corner a height of 2 1 2 0 + 2 3 1 0 = 1 0 + 5 3 .
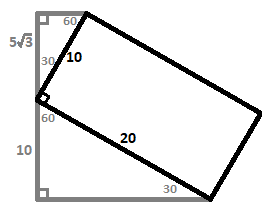
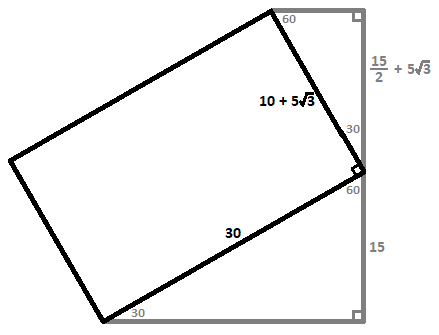
If we then rotate the result 3 0 ° parallel to the y z -plane, another two 3 0 ° - 6 0 ° - 9 0 ° triangles are formed with hypotenuses of 3 0 and 1 0 + 5 3 , giving the highest corner a height of 2 1 3 0 + 2 3 ( 1 0 + 5 3 ) = 2 4 5 + 5 3 ≈ 3 1 . 1 6 .
I found your solution to be kind of obscure and ambiguous. You did not explain why you reversed the order of the rotations, nor did you follow the type of rotation specified in the problem.
Log in to reply
Although the sequence of rotations that I describe in my solution are different than the sequence of rotations specified in the problem, the end result has the same orientation and position for the cuboid, and therefore the same altitude, and therefore the same solution. The advantage of using the sequence of rotations that I used, though, is that the axes of both of my rotations are perpendicular to the xy, xz, and yz planes, which made for easier calculations (both rotations can be visualized by looking at a side view and "tipping over" the cross-sectional rectangle).
This solution can be expressed in the form of matrices or trig, but the most elegant solution to me is to use quaternions to apply a rotation to a point p in 3D space. Because the quaternion product q p q − 1 , also called the Hamilton product of two quaternions, gives a rotation p ′ of vector p by angle a around unit vector u when quaternion q is equal to [ s i n ( 2 a ) + c o s ( 2 a ) * u ], we can calculate these rotations via quaternion products.
It can be seen that the point furthest from the origin will be the one to reach the highest, so we will apply the quaternion operations on that point, being p = ( 3 0 , 2 0 , 1 0 ) = 3 0 i + 2 0 j + 1 0 k The first rotation is a rotation of 30 degrees around the vector -j (or (0,-1,0)), giving us the quaternion q = . 9 6 5 9 + . 2 5 8 8 j , of the point p , which gives us the p ′ = 2 0 . 9 8 0 8 i + 2 0 j + 2 3 . 6 6 0 3 k . We get the next axis of rotation by rotating the unit vector i around the same axis, giving us the rotation vector u 2 = 0 . 8 6 6 i + 0 . 5 k . Then to rotate the point p ′ around u 2 by 30 degrees we use the quaternion q 2 = . 9 6 5 9 + . 2 5 8 8 ∗ u 2 By taking this final Hamilton product of q 2 p ′ q 2 − 1 we get the vector p ′ ′ = 1 6 . 6 5 0 7 i + 1 2 . 3 2 0 5 j + 3 1 . 1 6 0 3 k . Taking the coefficient for k will give us the answer to the highest point of the rotated shape, being 3 1 . 1 6 0 .
A more elegant solution would be to combine these two rotations into a single rotation by multiplying the two quaternions q and q 2 together before taking the Hamilton product (which I didn't do because I have a dislike for calculators and was dealing with some pretty messy numbers.) The quaternion q − 1 is the conjugate of the quaternion q and is found by negating all of the coefficients of the imaginary parts of the quaternion, much like a complex conjugate in two dimensions. Much more information on this type of spatial rotation can be found on Wikipedia . This is one of my first solutions, and the first one in which I attempted formatting, so feedback on my presentation (both solution itself and presentation) would definitely be welcome!
In the first rotation about Y axis, the point (30,20,10) shifts to new point (15√3-5, 20, 15+5√3).
In the second rotation about X axis, the above new point shifts to (15√3-5, 15(√3-1)/2, 10+15(1+√3)/2). Thus, the highest point is Z=10+15(1+√3)/2=30.4903.
Thus my answer is 30.4903. It is purely based on the rotation of point (30,20,10) by applying two rotations, first by (-30°) along Y-axis and the second by (30°) along X-axis. The cuboid is irrelevant in this picture.
On second thought, my second rotation has been applied incorrectly on the original edge along the X- axis of the original X-Y face.. The second rotation should be applied along the new edge along the new X-axis along the new X-Y face.
Therefore, my answer 30.4903 is different from the popular answer 31.16 given by others.
Attaching a right-handed coordinate frame to the cuboid, as shown in the picture above, we see that the 3 0 units edge is along the x -axis, the 2 0 units edge is along the y -axis, and the 1 0 units edge is along the z axis. We first rotate with respect to the y -axis by an angle of − 3 0 ∘ , where the sign is negative because rotation is clockwise. The second rotation is about the x -axis by an angle of 3 0 ∘ . This angle is positive because rotation about the x -axis is counter clockwise. The rotation matrix corresponding to the first rotation about the y -axis is given by:
R 1 = ⎣ ⎡ cos ϕ 1 0 − sin ϕ 1 0 1 0 sin ϕ 1 0 cos ϕ 1 ⎦ ⎤
and the rotation matrix corresponding to the second rotation about the x -axis is given by:
R 2 = ⎣ ⎡ 1 0 0 0 cos ϕ 2 sin ϕ 2 0 − sin ϕ 2 cos ϕ 2 ⎦ ⎤
If p 2 is the coordinate of a point with respect to the final coordinate frame (of the base) after the two rotations, then its coordinates with respect to the coordinate frame after the first rotation is p 1 = R 2 p 2 . Similarly, the point coordinates with respect the original coordinate frame is p 0 = R 1 p 1 = R 1 R 2 p 2 .
We thus have, with ϕ 1 = − 3 0 ∘ and ϕ 2 = 3 0 ∘ ,
R = R 1 R 2 = ⎣ ⎢ ⎢ ⎢ ⎡ 2 3 0 2 1 0 1 0 − 2 1 0 2 3 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 2 3 2 1 0 − 2 1 2 3 ⎦ ⎥ ⎥ ⎥ ⎤
Carrying out the above matrix multiplication, we obtain,
R = 4 1 ⎣ ⎡ 2 3 0 2 − 1 2 3 3 − 3 − 2 3 ⎦ ⎤
The highest point of the rotated cuboid is space diagonally opposite to the origin, so its coordinates are p 2 = ( 3 0 , 2 0 , 1 0 ) . Hence its coordinates in the absolute frame are:
p 0 = R p 2 = 4 1 ⎣ ⎡ 2 3 0 2 − 1 2 3 3 − 3 − 2 3 ⎦ ⎤ ⎣ ⎡ 3 0 2 0 1 0 ⎦ ⎤ = 4 1 ⎣ ⎡ 5 0 3 − 2 0 4 0 3 − 2 0 9 0 + 2 0 3 ⎦ ⎤ = ⎣ ⎡ 1 6 . 6 5 1 2 . 3 2 3 1 . 1 6 ⎦ ⎤