Rotating Back Home
Starting with a point at ( 1 , 0 , 0 ) on a unit sphere, three successive rotations about the z -, x -, and y -axes each by θ = 9 0 ∘ will bring it back to the point of beginning.
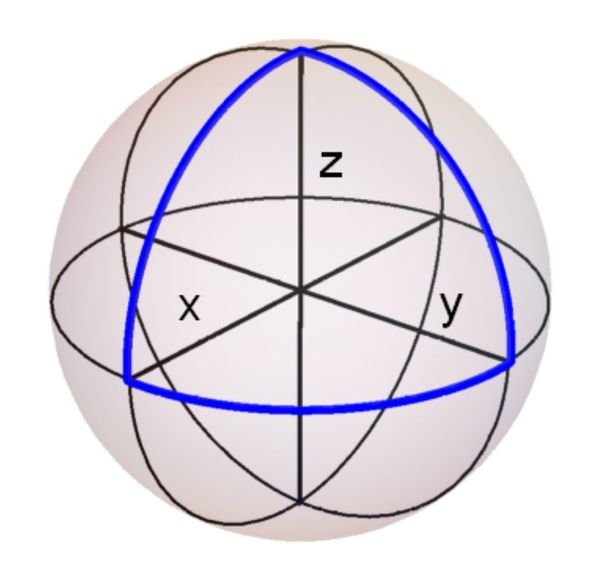
What's the minimum number of rotations (which can be in any sequence) necessary to return to point ( 1 , 0 , 0 ) exactly , if the following conditions are met?
- All rotations are about the x -, y -, or z -axis by the same angle θ < 9 0 ∘ in either direction.
- The same axis of rotation is not used twice in succession, regardless of direction.
- The last rotation is not the same as the first—i.e. the two rotations must be about different axes—so that there are as many corners as there are steps.
- The path may cross itself.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You've made this problem a lot more interesting, David.
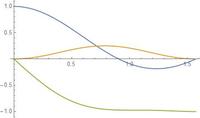
With the sequence of rotations ( y + , x + , y + , x + ) , no angle will get you ( 0 , − 1 , 0 ) . A little bit of plotting shows this, showing x , y , z for θ = 0 to 9 0 .
Log in to reply
I meant ( 0 , 1 , 0 ) , not ( 0 , − 1 , 0 ) . I'll edit that.
David, I'm going to have to repost this problem as I realize now that there is a shorter solution. I'll do that probably tomorrow.
Log in to reply
Oh, interesting!
Log in to reply
I've decided not to delete this problem, because you've brought up a far more interesting solution, and I'm still thinking about that. I could impose some more restrictions on this problem so that you'd have about the only solution, but that would be really hard on the readers.
I just want to keep this thread alive about this special angle. It seems like a miracle.
Log in to reply
@Michael Mendrin – Okay, sounds like a good plan!
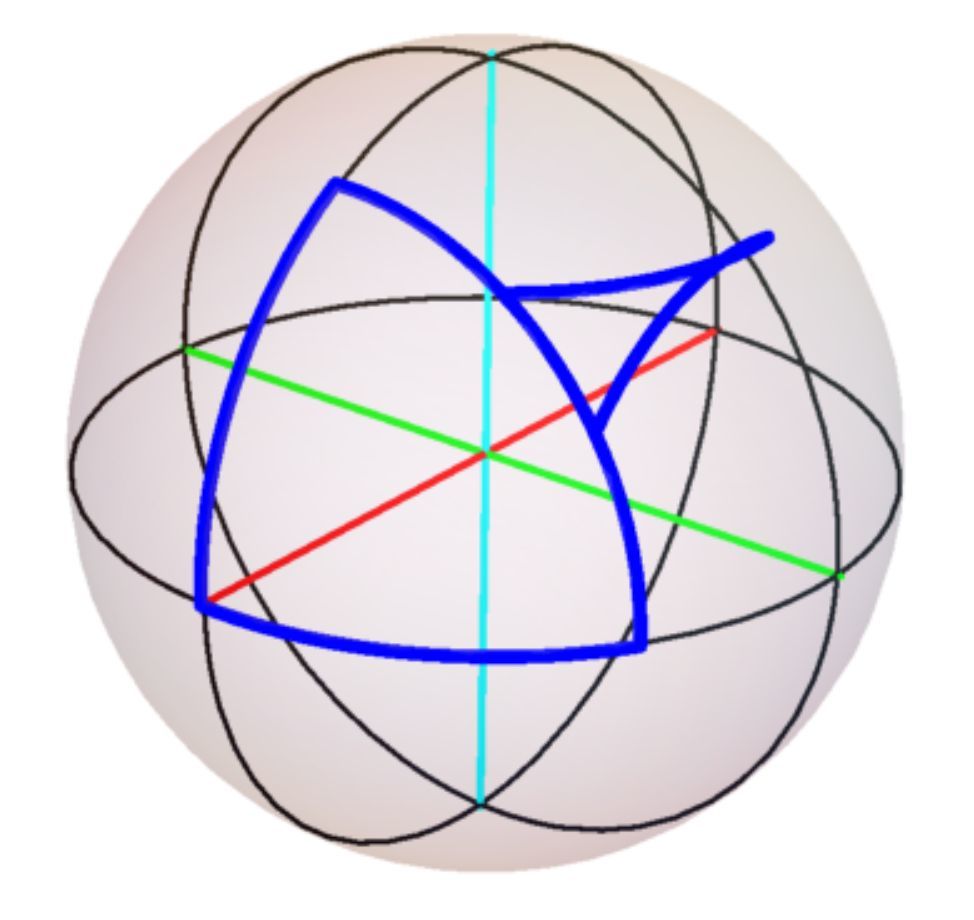
Here's one solution with six rotations:
The exact angle here is
θ
=
A
r
c
T
a
n
(
9
1
(
−
2
+
3
1
9
−
3
3
3
+
3
1
9
+
3
3
3
)
(
1
+
3
1
9
−
3
3
3
+
3
1
9
+
3
3
3
)
)
=
0
.
9
9
5
9
7
.
.
.
or approximately
5
7
.
0
6
4
9
degrees.
The sequence of rotations is ( y + , x + , y + , z + , x + , z + )
The following are the rotation matrices for rotation about axes x , y , z respectively:
⎝
⎛
1
0
0
0
C
o
s
(
θ
)
−
S
i
n
(
θ
)
0
S
i
n
(
θ
)
C
o
s
(
θ
)
⎠
⎞
⎝
⎛
C
o
s
(
θ
)
0
−
S
i
n
(
θ
)
0
1
0
S
i
n
(
θ
)
0
C
o
s
(
θ
)
⎠
⎞
⎝
⎛
C
o
s
(
θ
)
−
S
i
n
(
θ
)
0
S
i
n
(
θ
)
C
o
s
(
θ
)
0
0
0
1
⎠
⎞
David Vreken has an extremely interesting solution that isn't symmetric, involving a very special angle. I wonder if there are any shorter paths that doesn't involve symmetry.
An angle I found was θ ≈ 5 1 . 8 2 7 ° , where one possible solution of 1 0 rotations is ( y + , x + , y + , z + , x − , y − , z − , y − , x − , z + ) (where x + is a rotation around the x -axis one way, and x − is a rotation around the x -axis the other way, and so on). I don't really have a proof for this, other than I noticed this angle would be a likely candidate as 4 rotations would bring the point to a different axis (for example, ( y + , x + , y + , x + ) ), and 1 0 rotations was my best attempt with this angle to get the point back to ( 1 , 0 , 0 ) .
Log in to reply
I'll check to see if i can find the exact angle with that approach.
Log in to reply
Wow, θ = sin − 1 ϕ − 1 , where ϕ is the golden ratio. How cool is that?
Log in to reply
@David Vreken – That is cool, even though you really mean θ = c o s − 1 ϕ − 1 . Let me see if I can understand why.
Log in to reply
@Michael Mendrin – Wow again, I'm truly impressed with your solution, how did you even find it? It does return to ( 1 , 0 , 0 ) exactly, even though it doens't seem obvious why it should. This is a much more interesting solution than the one I posted here. But it does make a symmetric move over the x z plane which determines the angle.
Log in to reply
Log in to reply
@Michael Mendrin – Nice picture! I am going to post my solution along with this picture (if you don't mind) as a separate solution so others can see it more easily.
@Michael Mendrin – I was able to visualize that it was possible to move the point to ( 0 , 1 , 0 ) by the 4 rotations ( y + , x + , y + , x + ) ) at approximately θ ≈ 6 0 ° . I used a Python computer program to narrow down that angle to θ ≈ 5 1 . 8 2 7 ° . I assumed (either by intuition or just dumb luck) that since I could move the point from one axis to another using θ ≈ 5 1 . 8 2 7 ° in 4 moves, I could jump from axis to axis and eventually get back to the starting axis by a multiple of 4 . I went back to my Python computer program to see if I could grind out a combination of 8 rotations to work with θ ≈ 5 1 . 8 2 7 ° , and when that didn't work I tried 1 2 , only to discover that 1 0 works (even though it is not a multiple of 4 , but my theory is that it takes a shortcut through a working 1 2 route). So unfortunately this is not a very good mathematical proof but just an educated guess that worked out for me.
@Michael Mendrin – I did mean θ = sin − 1 ϕ − 1 . Note that θ = sin − 1 ϕ − 1 = cos − 1 ( ϕ − 1 ) = 9 0 ° − cos − 1 ϕ − 1 ≈ 5 1 . 8 2 7 ° .
I numerically verified your solution of 6 rotations, although 0 . 9 9 5 9 7 ≈ 5 7 . 0 6 4 9 ° , not 4 4 . 8 8 4 3 ° .
Numerically, I did not find any solutions for less than 6 moves with the new constraints (with the aid of a computer). Of course, this would not suffice as a proof as it assumes I found all the roots, which I probably didn't.
However, I found another angle for 6-moves: θ = 0 . 4 8 8 1 4 7 , and using the same notation as you did, a sequence of ( y − , x + , z + , x + , y + , x + )
Log in to reply
Poon, even though I found that 6 move solution purely for symmetry reasons, it's otherwise just about impossible to analyze this problem without the use of the computer. I have "good reason" to believe that there are no 3, 4, 5 move solutions, but proving it rigorously is something else.
Let me check your 6 move solution... hmm.
Your angle allows for a 5 move solution, but it returns to the beginning rotating about the same axis. I'm having trouble duplicating your 6 move solution.
Log in to reply
The angles seem to appear for different number of moves. For instance, the angle you found also has a 7 move solution. Perhaps there is an easier way to view this problem.
Log in to reply
@Julian Poon – oh I would love to hear of an "easier way to view this problem"
Perhaps there was something wrong with my code, I'll check it and update. It was able to find your solution though, so my code was probably accepting more solutions than it shouls be
Log in to reply
@Julian Poon – The convention I'm going by is + for clockwise and - for counterclockwise, when the origin is seen from the positive part of the x, y, z axes. Any convention will do, but it's a matter of being on the same page.
ANY unusual solution would be appreciated
Log in to reply
@Michael Mendrin – I've got the sequence wrong. It should be ( y + , x − , z − , x − , y − , x − ) .
And indeed it will be 5 moves, if not for the x − which does pretty much nothing.
I found a flaw in my reasoning... will correct it shortly... sorry
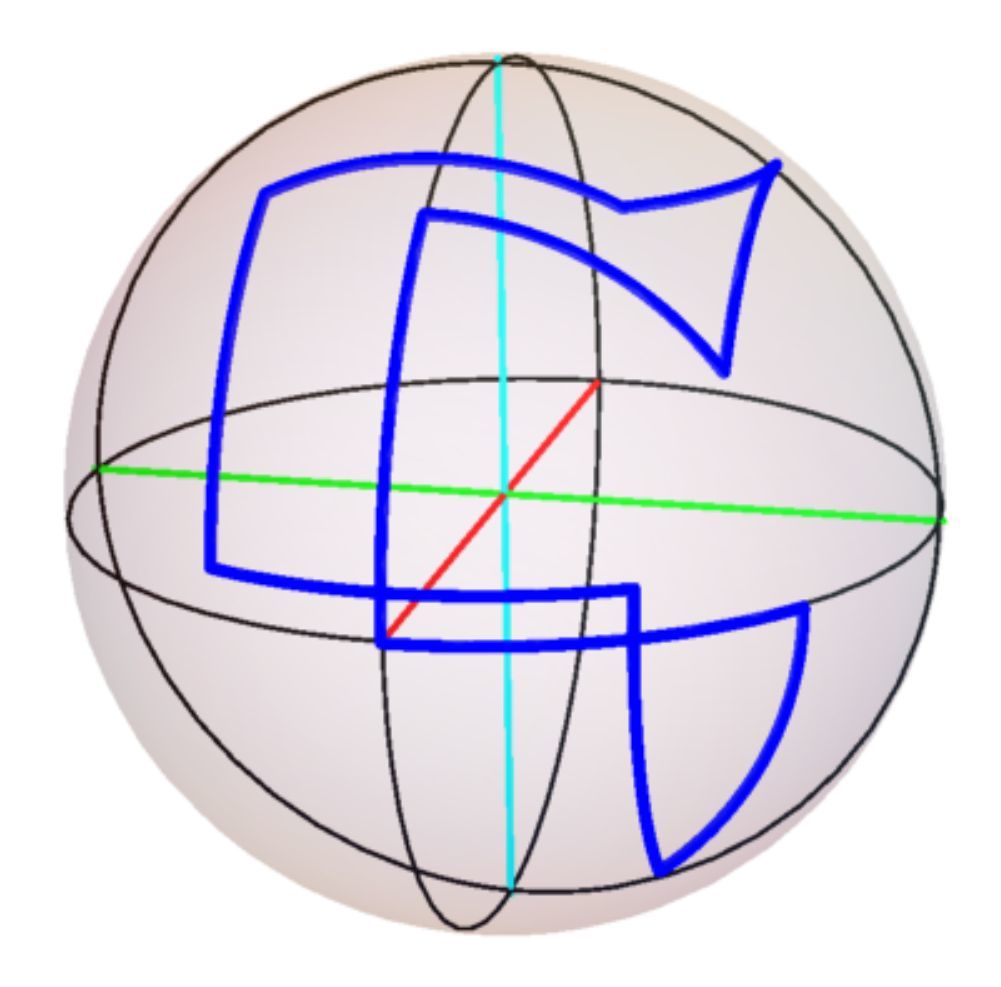
This is not a complete solution, as it does not show that 6 rotations is the minimum, but it does show that 6 is possible:
We can show that 6 rotations is possible without having to find a specific angle by seeing that there exists an intersection point between arcs along the surface of the sphere that are the locus of different combinations of 3 rotations. For example, in the picture from @Michael Mendrin 's solution, the third transformed point would be the intersection of the two arcs that are locus of points for rotations ( y + , x + , y + ) and ( z − , x − , z − ) (where x + is a rotation around the x -axis one way, and x − is a rotation around the x -axis the other way, and so on) that start at ( 1 , 0 , 0 ) for any angle θ < 9 0 ° . Reversing ( z − , x − , z − ) gives ( z + , x + , z + ) , and (making sure that it follows the given requirements) this gives the combined solution of ( y + , x + , y + , z + , x + , z + ) , which has 6 rotations.
This is not a minimum solution, but an interesting asymmetric solution involving the golden ratio:
One possible way to get the point back home with 1 0 rotations is ( y + , x + , y + , z + , x − , y − , z − , y − , x − , z + ) (where x + is a rotation around the x -axis one way, and x − is a rotation around the x -axis the other way, and so on), at an angle of θ = sin − 1 ϕ − 1 = cos − 1 ( ϕ − 1 ) ≈ 5 1 . 8 2 7 ° , where ϕ is the golden ratio equal to 2 1 + 5 .
Here is a picture courtesy of @Michael Mendrin :
I don't really have a proof for this, other than I noticed that this angle would be a likely candidate as 4 rotations brings the point to a different axis (for example, ( y + , x + , y + , x + ) to ( 0 , 1 , 0 ) ), and in my attempt to use a series of these 4 rotations in a combination to jump from one axis to another to get back to ( 1 , 0 , 0 ) , I found (with the help of a computer program) that 1 0 rotations was the minimum number needed with the given angle θ = cos − 1 ( ϕ − 1 ) . Perhaps someone can explain how this works out?