Rotating is Your Answer

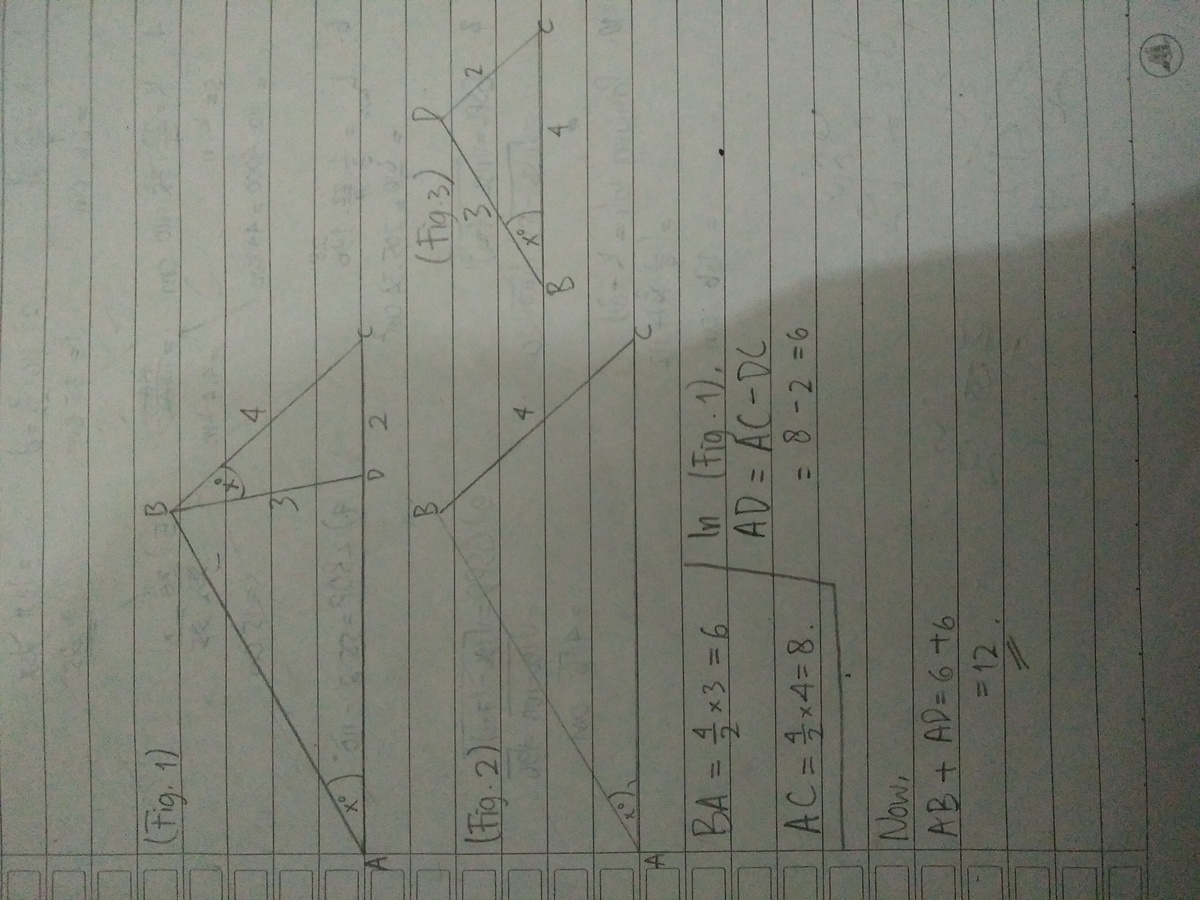
Look at $\triangle ABC$ and $\triangle BDC$ . We know that $\angle BAC = \angle DBC$ , look closely and you will see that $\angle BCA = \angle BCD$ . This conclude that $\angle ABC = \angle BDC$ . So $\triangle ABC$ and $\triangle BDC$ are similar.

From the figure, we can see that $\dfrac{4}{2} = \dfrac{AD + 2 }{4}$ and $\dfrac{AB}{4} = \dfrac{3}{2}$

Solving the equations lead us to the answer where $AD = 6$ and $AB = 6$

$AD + AB = 6 + 6 = \color{#D61F06}{\boxed{12}}$

similarity test and then (3/2) 3+((4/2) 3-2)=11.5 round up 12