Rotating Mass-Spring System
In the x y -coordinate system, a 1 k g mass is attached to one end of a massless ideal spring. The other end of the spring is fixed at the origin. The spring constant is k = 1 0 N / m , and the spring's unstretched length is 1 m .
The mass is initially being held in the air horizontally at ( x , y ) = ( 1 m , 0 m ) , and then is released so that gravity pulls it downwards. How far is the mass from the origin right at the moment it first crosses the (vertical) y -axis?
Details and Assumptions:
- Give your answer in meters, to 2 decimal places.
- There is an ambient downward gravitational acceleration of 1 0 m / s 2 .
- For the sake of this problem, assume that the spring can be stretched to great lengths.
The answer is 3.53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Nathan Sheely . The solution could have been done with Cartesian coordinates. Using differential equations for the horizontal and vertical motion. These equations lead to the same answer (which is what I did much like Arjen's answer but I used RK4 for integrating the accs to velocities). The beauty of the polar motion approach is that it avoids the (x|y)/sqrt(x x+y y) terms. The radial equations are a radial acc term less the centripetal acc. Whilst the tangential equ. has terms for the angular acc and the coriolis acc.
@Steven Chase , nice problem. I tried the numerical method with a 0.1s time step and it got a value of x=-0.014 (14mm left of center) and y= 3.530 at 1.1s. This quite good, especially as the "x" steps are about 200mm in the horizontal near the solution. It is just plausible to have done this is in the pre-digital age at this sort of step size. Using square and sqrt tables, or sin and cos tables. I am just old enough to have done "high school" applied maths without a calculator; a slide rule and a book of tables were the tools, the former was quicker but less accurate.
Log in to reply
I'm impressed that a time step of 0.1 s worked so well. A team of "calculators" could have done this in relatively short order, had the outcome of World War I depended on it or something (ha ha).
Thanks for the solution. We all used numerical methods. How solvable do you suppose this would have been 100 years ago?
Superb solution. I like your approach to the problem, the way you first wrote the force in the x and y-direction and then breaking the acceleration in the radial and tangential direction.
The main thing to notice here is the ball does not take a perfect circle. That is why the radial acceleration is r ¨ − r θ ˙ 2 and the tangential acceleration is r θ ¨ + 2 r ˙ θ ˙ .
Hi, I don't understand how to get the equations that were obtained by taking the radial and transverse components of the initial x-y coordinate equations of motion, or how to obtain the time (or the r at that time) from those equations and the initial conditions. If someone could clarify those steps for me or point me in the right direction to understanding the solution, I would appreciate it.
Log in to reply
Here's my interpretation of the dynamics in polar coordinates. I think it's the same as what Mark has, except for the different angular convention. It makes use of Lagrangian Mechanics.

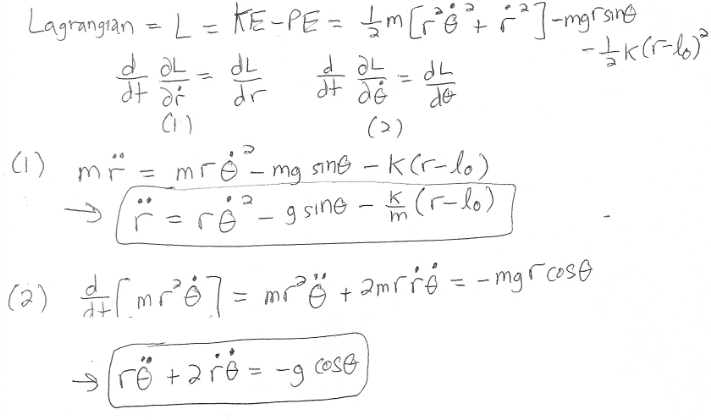
With x = ( − r cos θ r sin θ ) we differentiate twice to obtain x ˙ x ¨ = r ˙ ( − cos θ sin θ ) + r θ ˙ ( sin θ cos θ ) = r ¨ ( − cos θ sin θ ) + 2 r ˙ θ ˙ ( sin θ cos θ ) + r θ ¨ ( sin θ cos θ ) − r θ ˙ 2 ( − cos θ sin θ ) = ( r ¨ − r θ ˙ 2 ) ( − cos θ sin θ ) + ( r θ ¨ + 2 r ˙ θ ˙ ) ( sin θ cos θ ) Plug this into the original equation, and take components; in other words, take the inner product with ( − cos θ sin θ ) and ( sin θ cos θ ) .
There is not room here to go into the theory of numerical solution of differential equations - you will need to find a book.
I don't understand why the calculations have to be so complex? What I did was equate the total energy at the origin and the point where the ball crosses the vertical axis, the Kinetic energy I found out with centripetal acceleration at x = 0. This gave me a simple quadratic equation on t, the extended length, which came out for me to be (1+((7)^(1/2)))/2. Which gave me the final answer 2.82 metre. If someone could tell me where I went wrong, thanks.
Also, at any point, the sine component of gravitational acceleration is the tangential acceleration, no? That could be related to the change in length of the spring by relation of centripetal acceleration with k't'. If you could also tell me if you think that leads to something meaningful, I will appreciate it.
Log in to reply
Did you take the centripetal acceleration as r v 2 and tangential acceleration as r α ? If that is so then it is incorrect. Can you show the equations you make?
Log in to reply
Had no need for tangential acc., but can you tell me why v^2/r is wrong
Log in to reply
@Nabh Spandan – Ok, The particle is not moving in the perfect circular motion and therefore, it will suffer a Coriolis force. That is why the radial/centripetal acceleration is r ¨ − r θ ˙ 2 and the tangential acceleration is r θ ¨ + 2 r ˙ θ ˙ .
The second last equation in Mark's solution is the equation of the centripetal acceleration.
Not that SHM didn't occur to me, my method seems simpler because I don't have to deal with complicated expressions or big calculations, yes?
Log in to reply
The energy equation (in Cartesian coordinates) states that 2 1 ( x ˙ 2 + y ˙ 2 ) + 5 ( x 2 + y 2 − 1 ) 2 = 1 0 y Since x ˙ , y ˙ , x ¨ and y ¨ are nonzero when x = 0 , these equations are too complicated to handle in the manner you propose.
Log in to reply
shouldn't we include I w 2 / 2
Log in to reply
@Asif Hasan – No, only a point particle is involved, so there is no moment of inertia.
Whilst conservation of energy applies. I.e. The gravitational energy mgh becomes the mechanical strain energy in the spring (1/2kx^2) and the motion energy 1/2mv^2. However the velocity and y-position are unknown at x=0. Thus the need to solve the pair of 2nd order diff eqns.
@nabh spandan: I did the same thing and got 2.82 as the answer. No idea what's wrong in that method of energy conservation.
Log in to reply
May be it is because tangential velocity is changing and not constant, so the force balancing equation becomes invalid.
Beautiful solution.
If k were very large, the problem would reduce to a large-amplitude pendulum, which has no closed algebraic solution. Therefore we have no hope of accomplishing that here. If numerical methods are needed anyway, we might as well do a numerical simulation.
(Mark's approach with polar coordinates can be convenient, but the price we would pay here consists of sines and cosines. In Cartesian coordinates, the most involved mathematical operation is the square root.)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
|
Output:
1 |
|
Thanks for the solution. I like your observation that with high k, this reduces to a large-amplitude pendulum problem. I did it the same way you did but with a microsecond time step and Euler integration.
import math
L = 1.0
m = 1.0
g = 10.0
k = 10.0
x = L
y = 0.0
vx = 0.0
vy = 0.0
ax = 0.0
ay = -g
t = 0.0
dt = 10.0**(-6.0)
while x >= 0.0:
x = x + vx * dt
y = y + vy * dt
vx = vx + ax * dt
vy = vy + ay * dt
r = math.hypot(x,y)
delx = 0.0 - x
dely = 0.0 - y
u1x = delx / r
u1y = dely / r
Fsmag = k * math.fabs(r - L)
Fsx = Fsmag * u1x
Fsy = Fsmag * u1y
Fx = Fsx
Fy = Fsy - m*g
ax = Fx / m
ay = Fy / m
t = t + dt
print t,y
# Results (t, y)
# 1.09173 -3.53001388952
Log in to reply
I think Arjen has used the midpoint method in his solution. How does the Euler's method compare with the midpoint method time-complexity wise? Which method gives more accurate value for the same step size?
Log in to reply
Indeed I use the midpoint method for position calculations. v ( t + Δ t ) ≈ v ( t ) + a ( t ) Δ t ; x ( t + Δ t ) ≈ x ( t ) + 2 v ( t ) + v ( t + Δ t ) Δ t .
It is easy (since the old and new velocity are readily available), and obviously an improvement over the most primitive approach. For instance, for constant-acceleration motion this approach gives exact values.
If I make my step size 1 0 − 6 (as Steve did) I get the more accurate answer of 3 . 5 3 0 0 1 .
Log in to reply
@Arjen Vreugdenhil – This is nice, just the small modification to the primitive method make the simulation more stable. If the midpoint method is used to calculate velocity also, then it would give exact results for linear acceleration too.
The trapezoid (midpoint) method is better for a given step size. The interesting thing too is that these different methods have different levels of numerical stability. I posted a problem on this a while back.
https://brilliant.org/problems/numerical-stability-of-eulers-method/?ref_id=1343388
Log in to reply
@Steven Chase – Right, I get it. The midpoint method takes into account the old as well as the new value, so it is more stable compared to the Euler method. On the other hand, the Euler method is a bit easier to implement.
Log in to reply
@Pranshu Gaba – Another interesting thing is that the stability depends on whether the method is explicit or implicit. Examples of explicit and implicit Euler methods are below:
E x p l i c i t : y k = y k − 1 + y k − 1 ′ Δ t = y k − 1 + f ( y k − 1 , u k ) Δ t I m p l i c i t : y k = y k − 1 + y k ′ Δ t = y k − 1 + f ( y k , u k ) Δ t
The explicit method solves for y in terms of the previous value of y and the present value of the forcing function u , both of which are known. For the implicit method, we see that y k is on both sides of the equation, and if the function f is non-linear, it can be considerably harder to solve than the explicit method. But the advantage is that the implicit method has better numerical stability.
The quarter period of a simple pendulum, which swings from horizontal to horizontal (through an arc of π ), does have a closed form. If the length of the pendulum is a , then this time is 2 g a ∫ 0 2 1 π cos θ d θ = 8 g a B ( 4 1 , 2 1 ) = 4 1 π g a Γ ( 4 1 ) 2
Log in to reply
That is true, although one can hardly call Γ ( 4 1 ) "algebraic"... It stands to reason that the additional oscillation would only complicate the integrand and get us even farther afield than beta and gamma functions.
Log in to reply
What do you want to understand by "algebraic"? Are you only going to include functional expressible by radicals? If so, not much can be expressed that way. If you start including transcendental functions like the trig functions, why stop there? To say that Γ is more odd than tan is just a matter of habit...
Log in to reply
@Mark Hennings – I think a more useful criteria is whether or not you can come up with a formula which allows you to calculate the behavior at a particular time, without being concerned with any other point in time. This has been described as "computational reducibility" - the ability to shortcut a problem.
Log in to reply
@Steven Chase – Of course. The time taken for a simple pendulum to reach any angle from a stationary horizontal point can be expressed in terms of an elliptic integral of the first kind, a transcendental function just as computable as any other!
I know the elliptic integrals are readily computable because I once helped an architect design a bridge, and I implemented the necessary elliptic integral calculations on a very early version of Excel.
Plot of the trajectory, step 10ms, 0-2s.
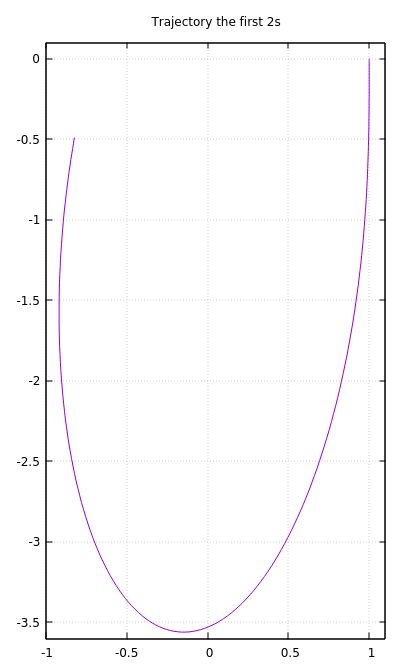
How do you draw this graph?
Made a simple text file from the output of the numerical solving program. Then used GNUplot to plot the x and y positions for the 200 steps. Once I had the GNUplot setting looking right, I asked it to dump to graphics as a PNG file.
Motion after about 2s will depend on what assumptions you make about the spring's behavior; does it apply an outward radial force to the weight or does it go slack?
Arjen V posted the source code and you could add a simple print x,y at the top of the while loop body. I'm sure GNUplot could handle the 10^6 lines of data or you could drop the time step to 1ms.
Log in to reply
Nice graph, there is hardly any symmetry in it. Do you think the motion of the particle will be periodic? That is, will it return to (1, 0) with velocity 0 after some time?
Log in to reply
Well I tried longer simulations. With the spring going slack: the simulations show a simple parabola trajectory inside the unit semi circle near the top. There was no regular pattern completely chaotic as far as I could tell up to a few hundred bounces.
Likewise with a spring capable of pushing when compressed, there was no pattern, but the paths were all more or less on average in the form of a deep semi ellipse similar to the initial 2s. The paths were on average rather similar whilst no paths were identical there is a remote chance that one of them might eventually get very close to the starting point. I believe that when chaotic systems center around a typical path this path is known as the basin of attraction of the hidden attractor.
Log in to reply
@Ed Sirett – Could this be because we are taking discrete time points which have small error in each time step, which could lead to large errors after many steps in the simulation? This system does look chaotic, being a spring pendulum. Small changes in the initial conditions could lead to a very different trajectory.
By the way, here's an interesting page with animations of various kinds of chaotic system made using springs and pendulums.
Log in to reply
@Pranshu Gaba – I don't think this is the integrating error. People have got the same result with different methods and time or angle steps. I think this a genuinely chaotic system, even the orbit of 3 bodies is chaotic, or even a rigid two bar linkage. It is surprising that a such simple and idealised system can be so complex in its motion.
Log in to reply
@Ed Sirett – Yes, I agree it is a chaotic system which moves in a complex path. It would have been nice if it had some kind of a simple periodic motion.
@Ed Sirett – This shouldn't be a chaotic system. It does produce a bird's nest pattern in it's trajectory...
If r is the distance of the mass from the origin, and θ the angle that the spring makes with the downward vertical, then the equation of motion of the system is x ¨ = 1 0 ( r − 1 ) ( cos θ − sin θ ) + 1 0 ( − 1 0 ) where x = ( − r cos θ r sin θ ) is the position vector of the mass, and the canonical unit vectors point horizontally and vertically up. Taking radial and transverse components, we obtain r ¨ − r θ ˙ 2 r θ ¨ + 2 r ˙ θ ˙ = − 1 0 ( r − 1 ) + 1 0 cos θ = − 1 0 sin θ together with the initial conditions r ( 0 ) = 1 , θ ( 0 ) = 2 1 π , r ˙ ( 0 ) = θ ˙ ( 0 ) = 0 . Solving these equations numerically, we find that θ = 0 for the first time when t = 1 . 0 9 1 7 3 , at which time r = 3 . 5 3 0 0 1 .