Rotation 1
A thin spherical shell of mass 6 k g and radius 6 c m is hit sharply by a cue at a height H ( c m ) from the centre of mass of the shell.
Find H ( in cm ) such that shell does not slip over the surface on which it is kept as shown below.
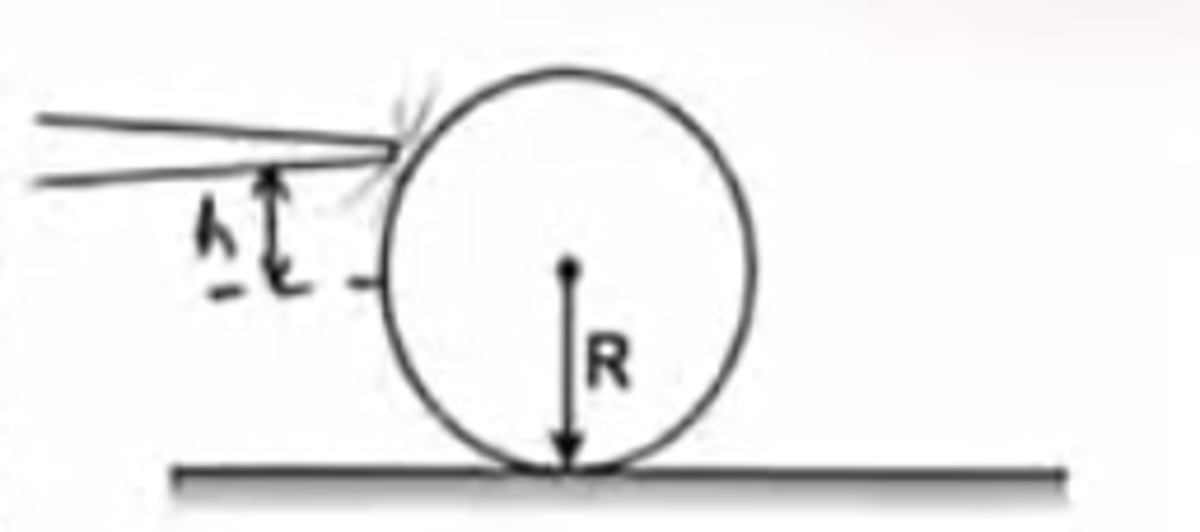
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Hey @Tapas Mazumdar @Spandan Senapati
Even if we assume no friction, the result comes same,you can verify it by conserving angular momentum abt com.What is the reason?
Log in to reply
How can you assume there's no friction? If there was no friction, the shell would not start rolling.
Log in to reply
It can start, the impulse provides the necessary torque abt COM.
Log in to reply
@Harsh Shrivastava – Only translational motion is possible in that case as the COM is not fixed. I suppose you also dealt with a question like this in some monthly test or AiiTS, where a solid sphere was struck with an impulse at some height and it was asked to comment about the further motion of the sphere.
Log in to reply
@Tapas Mazumdar – No bro, you may take a solid cylinder and then apply force at a distance R/2 above com.Then there will be no need of friction.
Log in to reply
@Harsh Shrivastava – Yes that's a misconception that friction is necessary for rolling..
Log in to reply
@Spandan Senapati – Thanks for letting me know about this. This was my misconception too.
Log in to reply
@Tapas Mazumdar – You are welcome.....Cheers
@Tapas Mazumdar – Tapas da, Solve this now, Related to the topics you were arguing on..
https://brilliant.org/problems/rotational-mechanics-3/
Log in to reply
@Md Zuhair – Actually I solved all your Rotation problems. This one, while I was on my phone, I mistapped the wrong option and ended up getting incorrect. All your other problems were integer or float answers so that error did not happen there.
Log in to reply
@Tapas Mazumdar – But this one is not the one with options
@Md Zuhair – I'm sorry. I see that this is an entirely different problem. Let's try.
Log in to reply
@Tapas Mazumdar – Oh it can be.. Actually i didnt saw what you were talking in the middle at last i saw that it was written
"Thanks for letting me know about this. This was my misconception too."
Here this refers to that rolling in smooth floor
Log in to reply
@Md Zuhair – Yes. That was actually my misconception. The problem that you referred to me is completely relevant to this issue.
Before that when you referred to me the link of that problem, I only saw the URL address and presumed that it was the 3rd problem of your Rotation problems. That one I did incorrect because of tapping mistake.
Log in to reply
@Tapas Mazumdar – Oh 3rd one means the one with Moment Of Inertia?
I know it feels very very very bad when a wrong option is clicked. It happened to me several times. SOMETIMES I MISTAKENLY CLICK DISCUSS SOLUTION!
I also know, I once asked Calvin sir, can you make it correct. I did it correctly and showed up the solution , but unfortunately he said that no its not possible to do such individual changes.
So bad Luck Bro.
@Harsh Shrivastava – So, is there some additional info that had to be provided with this problem because my assumptions satisfy the answer.
@Harsh Shrivastava – And to the vertical impulse if there was any that would be nullified by impulsive Normal reaction.....Such impulses I guess you mustnbe familiar like ball hitting an incline etc
Log in to reply
@Spandan Senapati – But what about it's torque, how can we neglect it about the point of contact, @Spandan Senapati
Log in to reply
@Harsh Shrivastava – Ok that's true.The Normal can't shift anywhere as its a sphere.So its mostly that we need to neglect that.Do you see a reason why that should be neglected..I think it depends on the external agent.He could hit the cue straight and the contact being quite small(areal)there is unlikely any slipping that one could suppose at the point of hit.So its safe to assume it.
No that's not true.Harsh is correct...Just a simple example.....A ball can roll on a frictionless surface..Friction comes to act to prevent any slipping and if by virtue of an external impulse you can prevent slipping its done.
Why is there no component of impulse in vertical direction?
Log in to reply
We are essentially not dealing with motion in the vertical direction here. The net impulse imparted however, has a vertical component; but since the vertical component points downward and downward motion is restricted, therefore the vertical component of impulse does not bring about change in momentum. If however, H was below the COM of the shell, things would've been quirkier I suppose.
Here, F d t is the horizontal component of impulse.
Log in to reply
So there's some error in your solution I guess, correct me if I am wrong though.
Your are not considering impulse about the point of contact due to vertical component of impulse imparted.
Log in to reply
@Harsh Shrivastava – I'm considering horizontal component of impulse.
Log in to reply
@Tapas Mazumdar – Yeah but during conservation of angular momentum , vertical component of impulse will also provide impulse abt the point of contact.
Log in to reply
@Harsh Shrivastava – Can you hint me the necessary steps to resolve this? Is my solution totally wrong?
Log in to reply
@Tapas Mazumdar – I think I have seen a similar question b4 where it was stated that assume impulse acts only in horizontal direction.
Let the impulse imparted by the cue be equal to F d t .
Using impulse theorem, we have
F d t = m v − m ( 0 ) = m v ⋯ ( 1 )
Using angular impulse theorem about the point of contact of shell with the ground, we have
F d t ( H + R ) = I ω − I ( 0 ) = ( I C M + m R 2 ) ω = ( 3 2 m R 2 + m R 2 ) ω = 3 5 m R 2 ω ⋯ ( 2 )
where I is the moment of inertia of the shell about the contact point of shell and the ground.
Dividing ( 2 ) by ( 1 ) we have
H + R = 3 v 5 R 2 ω
For pure rolling, we must have v = R ω . Thus
H + R = 3 v 5 R 2 ω = 3 5 R ⟹ H = 3 2 R = 3 2 ( 6 ) = 4 cm