Rotation Revision
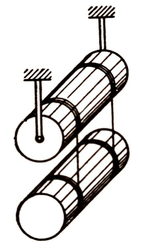 The arrangement shown in the figure consists of two identical uniform solid cylinders, each of mass
m
, on which two light threads are wound symmetrically.
The arrangement shown in the figure consists of two identical uniform solid cylinders, each of mass
m
, on which two light threads are wound symmetrically.
The tension of each thread in the process of the motion can be expressed as α m g , where g is the gravitational acceleration constant.
What is α ?
Assume that the friction in the axle of the upper cylinder is assumed to be absent.
This is one of my favorite problem taken from I.E Irodov, and now I am in search of different methods to solve this problem. I have solved the problem with the basic and straightforward method but I am in search of alternative methods.
The answer is 0.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong Thanks for sharing. By the way, try my latest problem.
Log in to reply
I have to relearn my uni stuff.
Log in to reply
@Chew-Seong Cheong I didn't understand the above sentence .
Log in to reply
@Talulah Riley – I study electrical engineering in university in 1978/82. I learnt Mechanics then and now I have forgotten. So I have to learn it again.
Your latest problem should have an answer of v 0 ≤ α R g and not ≥ . The higher the velocity the easier it will bounce not the other way. Please change it.
Log in to reply
@Chew-Seong Cheong – @Chew-Seong Cheong Yeah sorry, it is corrected now. Thanks
@Chew-Seong Cheong
whenever I upload a image, the image comes in the middle of the page.
How you made it to right side.? Thanks in advance.
Log in to reply
! [] (https://ds055uzetaobb.cloudfront.net/uploads/bFL8azslf6-b201016.png|height=250){: .right}
Change the default "center" at the end to "right". I have also added "|height=250" to size the figure. We can also use "|width". Try them.
Solving this problem using Lagrangian mechanics. Consider the initial separation between the cylinders' COM to be s . The system is set into motion, assume that the first cylinder rotates by an angle θ 1 and the second cylinder rotates by an angle of θ 2 . Therefore, as the string unwinds due to the system's motion, the string increases in length by R θ 1 + R θ 2 as the lower cylinder falls due to its weight. Note that s is treated as a constant.
Consider the axle of the first cylinder to be the origin. Then at any general time t , the y coordinate of the COM of the lower cylinder is:
y = − ( s + R θ 1 + R θ 2 )
The kinetic energy of the system is the sum of rotational kinetic energies of the two cylinders and the translational kinetic energy of the lower cylinder. This expression is:
T = 2 1 ( 2 m R 2 ) θ ˙ 1 2 + 2 1 ( 2 m R 2 ) θ ˙ 2 2 + 2 m y ˙ 2 ⟹ T = 4 3 m R 2 θ ˙ 1 2 + 4 3 m R 2 θ ˙ 2 2 + m R 2 θ ˙ 1 θ ˙ 2
The potential energy of the system is:
V = − m g y
Applying Lagrange's equations by treating θ 1 and θ 2 as generalised coordinates, gives the following equations of motion. I am leaving out this computation. The equations are:
1 . 5 θ ¨ 1 + θ ¨ 2 = R g θ ¨ 1 + 1 . 5 θ ¨ 2 = R g
Solving for the lower cylinder's angular acceleration about it's COM gives:
θ ¨ 2 = 5 R 2 g
Now, finally, one can compute the net torque experienced by the lower cylinder about the COG as follows. Let the tension in each string is T . Then:
2 T R = 2 m R 2 θ ¨ 2 ⟹ T = 0 . 1 m g
@Karan Chatrath
in the new problem, can't you give simply the value of
v
(
t
)
?
By the way what is
v
(
t
)
Is it
π
1
e
−
(
a
t
)
2
.
Log in to reply
In the wikipedia page I shared, skip to the section 'Definitions'. The function is defined there.
Log in to reply
@Karan Chatrath
Your function is
∞
at 0 and 0 at all other value?
Ye kaisa function hai?
Log in to reply
@Talulah Riley – Yes, that is the function. It is also called the impulse function. There is more than one way of solving this problem. If I would have given a standard source voltage function, this problem wouldn't be as interesting. There are a lot of conceptual insights to be found while solving this, according to me.
Log in to reply
@Karan Chatrath – @Karan Chatrath to time jaise hi 0.000001 second hoga voltage to zero ho jaayega. Phir kya karoge??
Log in to reply
@Talulah Riley – Yeh ab aap socho.
Also, search beyond that Wikipedia page that I shared. Working with this function is easier than you think. I am sure you will find atleast one very interesting property that you can easily use.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
What are doing currently. Like I am in class 12 , what you are doing?
You will not loose any personality information . Don't worry.
@Karan Chatrath Mujhe aap bas v ( t ) bata do, please. Baaki kaam phir mera
Let the tension of each thread be T and the moment of inertia of the cylinder be I and its radius be r . Then I = 2 m r 2 and the torque of the top cylinder is given by:
τ 2 T r ⟹ α 1 = I α 1 = 2 m r 2 α 1 = m r 4 T where α 1 is the angular acceleration of the top cylinder.
Similarly, for the bottom cylinder, 2 T r = 2 m r 2 α 2 ⟹ α 2 = α 1 . Now consider the translation motion of the bottom cylinder which is given by the downward force:
F z m g − 2 T m g − 2 T ⟹ T = m a = m a = m a = m ( α 1 r + α 2 r ) = 2 m α 1 r = 8 T = 1 0 m g where a is the resultant acceleration. As there is no slipping of the threads on the cylinders.
Therefore α = 0 . 1 .