Round and round they go
Three points A , B , and C are moving counterclockwise around a unit circle with periods 1 s , 2 s , and 3 s , respectively.
They started from the same position on the circle.
What is the maximal area of triangle A B C ?
The answer is 1.1965249.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
How about Equilateral triangle? its area is approximately 1.299.
Log in to reply
I thought of that too. But at the angular velocities of A , B and C , an equilateral triangle can never be formed.
Log in to reply
i see. nice solution.
how did you conclude that?
Log in to reply
@Aman Verma – I plotted the whole graph. If there exists the maximum will be the equilateral triangle. I solve the problem using the graph.
The periods in a 1:2:3 ratio does not imply the speeds in a 1:2:3 ratio but rather 1:1/2:1/3 or 6:3:2.
If the speeds are in a 1:2:3 ratio then an equilateral triangle can be formed: Multiply by 120 degrees.
It's a good thing we get 3 tries because that was my first try.
Did you take into account in the last step that arccos has 2 answers? In this case it worked out because ( sin ( 3 ϕ ) + sin ( ϕ ) − sin ( 4 ϕ ) ) is symmetric to ϕ = π (actually to the right of ϕ = π , it is negative of the left of ϕ = π , but area is always positive, so it should be the absolute value of the function anyways), so you only have to worry about solutions where ϕ is between 0 and π .
Log in to reply
I actually plotted out the entire graph. Yes, there is two solutions but of course one maximum area.
Log in to reply
Ok, nice solution by the way. I solved it exactly the same way except I used Gauss's shoelace formula to find the area.
I used Heron's formula for the area, but otherwise similar. It appears there is no nice closed form solution for the area, the angles, or the side lengths. If there were someone would have shared it by now. It felt like cheating to solve with a graphing calculator.
Log in to reply
You asked for it. Area=(sin(3arccos{1/48 (-10 - (97 (1 + i sqrt(3)))/(199 + 12 i sqrt(6063))^(1/3) + i (sqrt(3) + i) (199 + 12 i sqrt(6063))^(1/3))})+ sin(arccos{1/48 (-10 - (97 (1 + i sqrt(3)))/(199 + 12 i sqrt(6063))^(1/3) + i (sqrt(3) + i) (199 + 12 i sqrt(6063))^(1/3))}) -sin(4arccos{1/48 (-10 - (97 (1 + i sqrt(3)))/(199 + 12 i sqrt(6063))^(1/3) + i (sqrt(3) + i) (199 + 12 i sqrt(6063))^(1/3))}))/2 Ok fine, so it's not a nice closed form.
Log in to reply
Lol. Did that by hand, did you?
Actually, you can see what looks like the solution to a cubic or quartic equation, but with all the sines and arccosines.
I got the area as A = ( sin 4 x − sin 3 x − sin x ) / 2 . The extrema are at 4 cos 4 x − 3 cos 3 x − cos x = 0 , solved it with Wolfram Alpha. The solutions are coming in the form of x = n π , x = 2 ( n π ± 0 . 5 0 6 4 ) and x = 2 ( n π ± 0 . 0 9 1 9 9 ) .
Using Desmos, I animated the graph of the area of the triangle and synced it up with the moving points. Great solution!
https://www.desmos.com/calculator/dravidum7e
I did it almost identically to you. Thanks for posting.
Given the Coordinates of a triangle Area = [(x2-x1)(y3-y1)-(x3-1)(y2-y1)]/2 No need for heron's formula :)
既然周期之比为1:2:3,速度比为6:3:2。
现在换参考系,假设速度为3的点为静止,那么其他两个点的速度为3和-1,相等时间内划过的角度为3:-1。
我们知道,三角形面积公式S=ab sinC/2,那么既然三角形内接于单位圆,不妨将三个顶点与圆心相连,将三角形表示为三个三角形面积之和,即:
S=(sinx+sin3x+sin(2π-4x))/2 =(sinx+sin3x-sin4x)/2
分析这个函数,找到在2π内的极大值:1.196525
Of course... That's exactly what I was thinking.
Loved the approach! Thanks!
Kuch samajh nahi aa raha hai
I Think 接于单位圆,不妨将三个顶点与圆心相连,将三角形表示为三个三角形 Was a genious idea!!!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
> max area: 1.196524791219177
I haven't heard numpy before, what is it?
Log in to reply
A module for python that adds a lot of math relates things such as matrices
We begin by finding expressions to describe the location of each point at any given time.
We find that the coordinates of point A are described by ( cos 2 π t , sin 2 π t ) , point B by ( cos π t , sin π t ) , and point C by ( cos 3 2 π t , sin 3 2 π t ) , where t is equal to time, in seconds, after the initial moment where all three points were at the same location. (Note: This is working in radians, not degrees.)
Using this information, we can now find functions to describe the distance between each pair of points (or the length of each side of the triangle) at any given time.
The distance between two points on a graph is described by ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 .
Plugging in our expressions for the locations of each point, we find that the distance between points A and B is described by a ( t ) = ( cos t − cos 2 π t ) 2 + ( sin t − sin 2 π t ) 2 , points A and C by b ( t ) = ( cos 3 2 π t − cos 2 π t ) 2 + ( sin 3 2 π t − sin 2 π t ) 2 , and points B and C by c ( t ) = ( cos 3 2 π t − cos t ) 2 + ( sin 3 2 π t − sin t ) 2 .
Now that we have have described the length of each side of the triangle, we can use Heron's formula to find the area of the triangle at any given time.
Heron's formula states that the area of a triangle is described by s ( s − a ) ( s − b ) ( s − c ) , where a , b , and c are the lengths of the sides of the triangle, and s is the semiperimeter of the triangle, which is described by s = 2 a + b + c .
First we create a function to describe the semiperimeter by plugging in our functions for the length of each side of the triangle into the formula, creating s ( t ) = 2 a ( t ) + b ( t ) + c ( t ) .
Now we plug all of our functions into Heron's formula, resulting in f ( t ) = s ( t ) ( s ( t ) − a ( t ) ) ( s ( t ) − b ( t ) ) ( s ( t ) − c ( t ) )
This function models the area of our triangle A B C over time.
Now we simply find the maximum of the function.
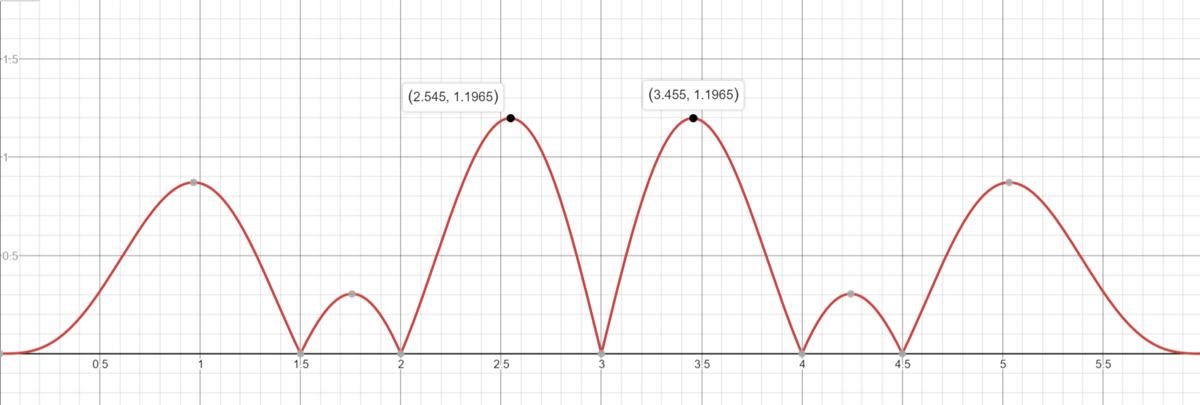
The maximum area of the triangle is about 1 . 1 9 6 5 , and occurs for the first time at about 2 . 5 4 5 seconds after the initial point, and for the second time at at about 3 . 4 5 5 seconds after the initial point.
Here is an outline of the approach I used: Let A = ( cos ( 2 π t ) , sin ( 2 π t ) ) , B = ( cos ( π t ) , sin ( π t ) ) and C = ( cos ( 3 2 π t ) , sin ( 3 2 π t ) ) and let A r e a ( t ) be the area of triangle A B C at time t .
The triangle A B C is one half of the parallelogram spanned by the vectors B − A and C − A , so:
A r e a ( t ) = 2 1 det ( B − A , C − A ) = 2 1 ∣ ∣ ∣ ∣ cos ( π t ) − cos ( 2 π t ) sin ( π t ) − sin ( 2 π t ) cos ( 3 2 π t ) − cos ( 2 π t ) sin ( 3 2 π t ) − sin ( 2 π t ) ∣ ∣ ∣ ∣ After some calculation we get A r e a ( t ) = 2 1 ( − sin ( 3 π t ) − sin ( π t ) + sin ( 3 4 π t ) ) . From here, we can proceed to find the maximum in the usual way, by setting d t d A r e a ( t ) = 0 , and so on.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
Simple and elegant.
I originally used the exact same method as David Wilbanks, but I ended up finding a way that is easier than the distance formula to find the distance between any pair of the three points. Lets call the measure of the central angle that intercepts the starting point and point C 's current position θ . The central angle that intercepts the starting point and angle A 's current position can be written as 3 θ , and similarly this angle for point B is 2 3 θ .
 Image not drawn to scale
Image not drawn to scale
If we think about the triangle that is formed with any two points and the center of the unit circle, we can use the law of cosines to find the distance between the points. In the case of point A and point C , we can first find that central angle that falls in the triangle is 2 θ , and using the law of cosines, we can now say that,
( d A , C ) 2 = 2 − 2 cos 2 θ .
This formula isn't wonderful to look at, so we can use some trigonometric identities to rewrite this as,
( d A , C ) 2 = 4 ( 2 1 − cos 2 θ ) ,
d A , C = 2 ( 2 1 − cos 2 θ ) ,
d A , C = 2 sin θ .
You can try using the same method for the other two selections of points, but the distances between the points end up being,
d A , B = 2 sin 4 θ , and
d B , C = 2 sin 4 3 θ .
Now we can use the Heron's formula to find the equation for the area of the triangle formed by the three points in any possible orientation, which is,
A = ( sin θ + sin 4 θ + sin 4 3 θ ) ( − sin θ + sin 4 θ + sin 4 3 θ ) ( sin θ − sin 4 θ + sin 4 3 θ ) ( sin θ + sin 4 θ − sin 4 3 θ )
Finally, we can graph this equation on a graphing calculator to find the maximum value for the area of the triangle formed by the three points, which is approximately 1 . 1 9 6 5 2 4 9 .
I also used almost the exact same method as David Wilbanks, but as I was contemplating the problem during the solving process, I considered changing to something more like what you have posted. Thanks for sharing.
Maximum area is for equilateral triangle when the first point rotated by 120 degrees, second by 240 and 3rd by 360 degrees.
This gives the area = ( 3√3 )/4 = 1.2 approx.
Wrong!!! There is no equilateral triangle formed if you take into account the periods of the three points...........See the comments in Sir Chew Seong Cheong's solution.....
Log in to reply
This is in the case of a period 1s, 1/2s and 1/3s. The solution, in that case, is much simpler. However, this case has periods 1, 2s and 3s.
You need the radius of the circle to solve this. Since $A=\frac {abc}{4R}$ and any such triangle has the same $R$, we need to maximize the product of the sides. This is attained when we have an equilateral triangle, which can indeed be made (as when the first particle has gone $\frac {1}{3} $ the way around, the second has gone $\frac {2}{3} $ the way, and the third has gone all the way around). Then we can use $A=\frac{1}{2}ab\sin {\theta} $ to calculate the area of one of the three identical triangles formed when you connect the center of the equilateral triangle to the vertices. This yields $3\cdot\frac {1}{2}(r)(r)(\frac{\sqrt{3}}{2})=\boxed {\frac {3r^2\sqrt {3}} {4}}$
I got the area as A = ( sin 4 x − sin 3 x − sin x ) / 2 . The extrema are at 4 cos 4 x − 3 cos 3 x − cos x = 0 , solved it with Wolfram Alpha. The solutions are coming in the form of x = n π , x = 2 ( n π ± 0 . 5 0 6 4 ) and x = 2 ( n π ± 0 . 0 9 1 9 9 ) . Once we calculate the area for a few of these solutions, we can identify the maximum.
I use GSP - with the three dots A, B, C moving in different speed (1s, 2s, 3s), start at the same point on a circle with radius 1 cm (=1 unit?). The maximum area of ABC obtained is 1.29. Where did i go wrong in constructing the circle and the points that it did not give the answer 1.19?
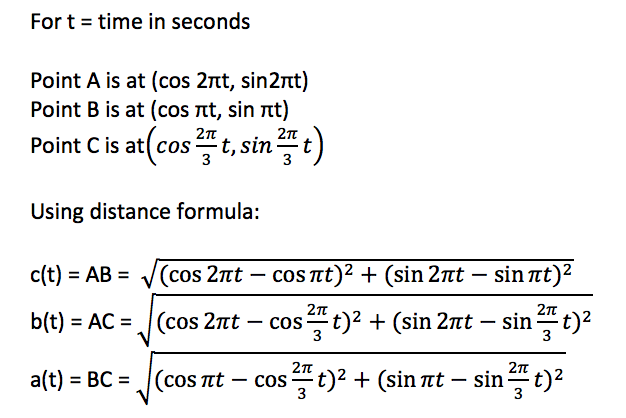

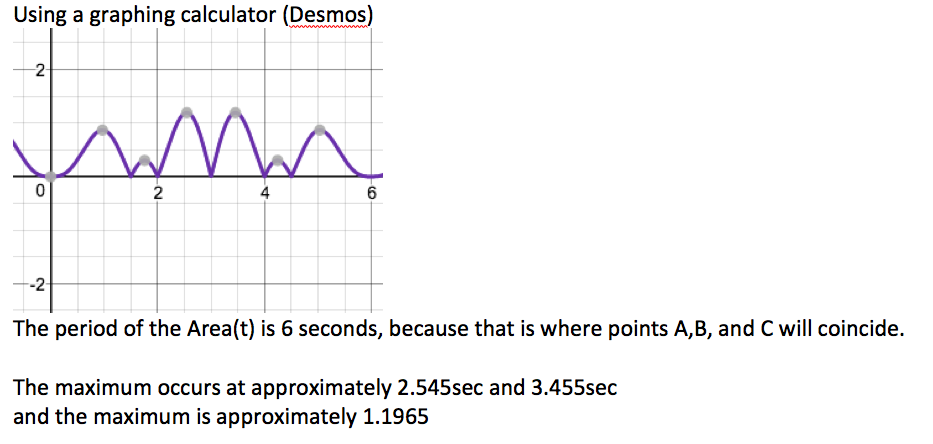
Let the angular velocities of A , B and C be ω A = 2 π rads − 1 , ω B = π rads − 1 and ω C = 3 2 π rads − 1 respectively. Instead of all three points are moving we can fixed one. say C , and find the relative position of A and B to C using relative angular velocities. Let the relative angular velocities to C of A and B be ω a = 2 π − 3 2 π = 3 4 π rads − 1 and ω b = π − 3 2 π = 3 π rads − 1 respectively.
Let the centre of the unit circle be O , ∠ A O C = θ a and ∠ B O C = θ b . We note that the area of △ A B C is given by:
[ A B C ] = [ A B O ] + [ B C O ] − [ A C O ] = 2 1 sin ( θ a − θ b ) + 2 1 sin θ b − 2 1 sin θ a = 2 1 ( sin ( ω a t − ω b t ) + sin ( ω b t ) − sin ( ω a t ) ) = 2 1 ( sin ( π t ) + sin ( 3 π t ) − sin ( 3 4 π t ) ) = 2 1 ( sin 3 ϕ + sin ϕ − sin 4 ϕ ) By formula A △ = 2 1 a b sin θ Let ϕ = 3 π t
The extrema of [ A B C ] occurs when
d ϕ d ( sin 3 ϕ + sin ϕ − sin 4 ϕ ) 3 cos 3 ϕ + cos ϕ − 4 cos 4 ϕ 3 ( 4 cos 3 ϕ − 3 cos ϕ ) + cos ϕ − 4 ( 8 cos 4 ϕ − 8 cos 2 ϕ + 1 ) 8 x 4 − 3 x 3 − 8 x 2 + 2 x + 1 = 0 = 0 = 0 = 0 Let x = cos ϕ and rearrange.
Solving for x by numerical method, we have:
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎧ x = 1 x = − 0 . 2 6 5 6 9 4 3 0 9 x = 0 . 5 2 9 3 8 9 2 x = − 0 . 8 8 8 6 9 4 8 9 1 ⟹ ϕ = 0 ⟹ ϕ = 1 . 8 3 9 7 2 0 3 7 3 ⟹ ϕ = 1 . 0 1 2 9 1 5 8 8 4 ⟹ ϕ = 2 . 6 6 5 2 8 7 1 1 5 ⟹ [ A B C ] = 0 ⟹ [ A B C ] = − 0 . 3 0 3 8 4 8 2 7 1 ⟹ [ A B C ] = 0 . 8 7 0 2 9 5 0 6 3 ⟹ [ A B C ] = 1 . 1 9 6 5 2 4 9 6 7
Therefore, the maximum area of △ A B C is 1 . 1 9 6 5 2 4 9 6 7 .