Same old block on the floor problem
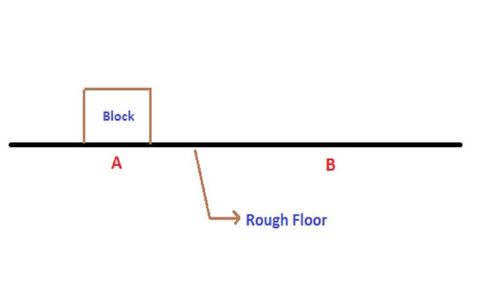 A block of mass
m
is placed on a rough horizontal floor at position
A
. This block is to be moved to position
B
under the application of a force of constant magnitude
F
, acting on the block. Find the
minimum
time (in seconds) for which this force should act on the block so that it just reaches
B
.
Round your answer to the nearest integer.
A block of mass
m
is placed on a rough horizontal floor at position
A
. This block is to be moved to position
B
under the application of a force of constant magnitude
F
, acting on the block. Find the
minimum
time (in seconds) for which this force should act on the block so that it just reaches
B
.
Round your answer to the nearest integer.
Details and Assumptions
- Consider the block as a point object and it is always in contact with the floor.
- m = 5 kg , F = 1 0 0 N , A B = l = 1 9 0 0 m .
- Acceleration due to gravity: g = 1 0 m/s 2 .
- Coefficient of friction: μ = 0 . 5 .
The answer is 6.996261607.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very, very nice! I was puzzled for a long time by whether the force could be acting at an angle or not. But then at last I thought that since the question didn't state the force was to be at an angle, the force would act parallel to the surface.
I have a doubt.Shouldn't the force vector be forward instead of at an angle?Please clarify.
Log in to reply
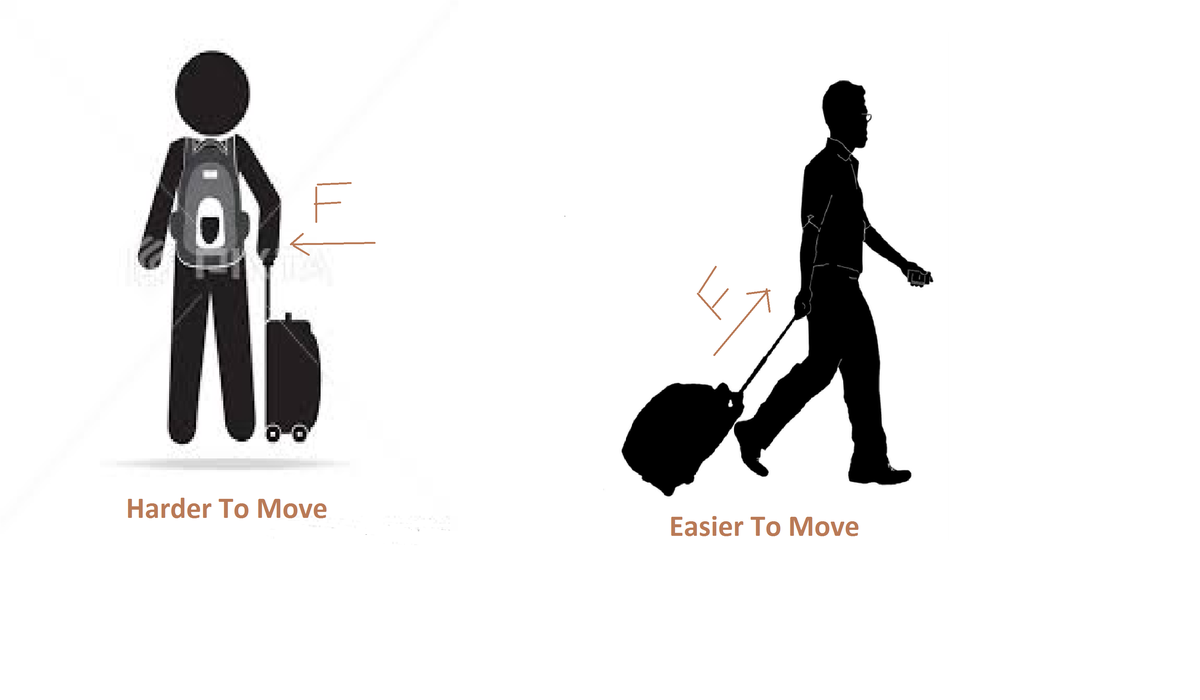
In this problem the main objective is to find the minimum time. So we have to find the maximum acceleration with which the force makes the body move in order to find the minimum time. If we assume the force to be acting horizontally then we will obtain a = 1 5 m s − 2 and t = 8 s , But how do you know this is the minimum time? So let's take a general case with the force acting at an angle like i did above and differentiate to find the minimum case. We will realize that when the force acts at θ = t a n − 1 ( μ ) , t = 7 s . This is the reason while pulling a luggage bag we pull it at an angle as it is easier than just pulling it horizontally as frictional force decreases.
Log in to reply
So that means at the angle of approx.26.5 degrees,the acceleration is maximum right .Thanks in advance.
I tried to solve it by energy conservation...
If AB=l , the work done by force F in time 't' be Fx ,if the block moves a distance 'x' in time 't'; So the work done Fx =work done by frictional force in the remaining distance...
Fx=umg(l-x);
Also acc. 'a' during which force was applied..... a=(F-umg)/m;
and 0.5at^2=x;
Combining these equations ;solve 't' t=[7.11]=7 sec
Instead of Fx=umg(l-x) it should be Fx=umgl, as the frictional force is acting on the body throughout the distance l. Then after substituting the values you will get 7.95 or 8 seconds which won't be correct as you assumed the force to be acting horizontally.
Log in to reply
Yes ..you are right that the force umg acts through the entire path l...but the work done by force F in time t is Fx ...if it travels 'x' distance in time t.....and the energy gained by the block after travelling the distance 'x'(till when the force acts) is Fx and now this energy is neutrallized by the frictional force over the REMAINING PATH (l-x) So Fx=umg(l-x);
Log in to reply
Kinetic energy gained by the block after travelling the distance 'x'(till when the force acts) is NOT Fx, it is (F-umg)x.
Log in to reply
@Rahul Badenkal – Ya i guess....probably you're right
Vertical Force balance equation:
N = m g − F s i n θ
Horizontal force balance equation:
F c o s θ − μ N = m a
F c o s θ − μ ( m g − F s i n θ ) = m a
a = m F ( c o s θ + μ s i n θ ) − μ g
To find maximum acceleration, differentiate and equate to 0
d θ d a = m F ( − s i n θ + μ c o s θ ) = 0
t a n θ = μ
a m a x = m F ( 1 + μ 2 1 + 1 + μ 2 μ 2 ) − μ g
a m a x = m F 1 + μ 2 1 + μ 2 − μ g
a m a x = m F ( 1 + μ 2 ) − μ g
Substituting the values we get
a m a x = 1 7 . 3 6 m s − 2
Now let the distance moved by the block while the force is acting on it be x and the velocity at that displacement be v and time taken to reach there be t .
Therefore,
2 a m a x x = v 2 ...............................( 1 )
For the 2nd part of the journey when only frictional force is acting
2 ( μ g ) ( l − x ) = v 2 ....................................( 2 )
From ( 1 ) and ( 2 ) we get
x = a m a x + μ g μ g l
Also for region 1,
x = 2 1 a m a x t 2
t = a m a x 2 x
t = a m a x ( a m a x + μ g ) 2 μ g l
Substituting the values we get
t = 7 s