Save Brilli
You have just started your summer job as a lifeguard at the beach, which has oversized ants leisurely swimming. You are on top of your lifeguard stand and notice that Brilli the ant is making distress signals some distance offshore, and you want to travel to Brilli in the quickest way possible.
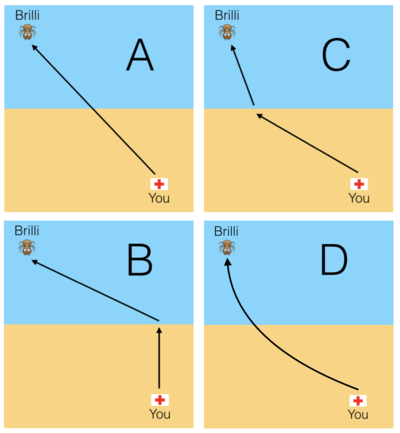
Knowing that you travel faster running over sand than you do swimming through water, which of the above best illustrates the quickest path to take?
Assume that the water is still, with no currents.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Problems with this,
1) C vs D If you where to construct a triangle with your hypotenuse the distance of what that was to be swimmed, i believe you would find D to be short, therefore faster. It is ridiculous to estimate the distance w/o a given a formula for the line/curve of the distanced swam or (gee I don't know) maybe if we had been told the distance... this problem is not mathematical.
Why are we saving an ant in the first place? We're human. While we were saving the ant, 10 people might have gotten injured due to our inattention.
We're lifeguards, not EPA officials.
Log in to reply
What you should ask in math class: "Why did Jim buy 60 watermelons? Does he need an intervention?"
I am not completely satisfied with the answer "C". "C" is the shortest path, but to be also the quickest one needs also the hypothesis "assume that the change of directions take place instantaneously, without a reduction of speed". It is clear that without this assumption there is not enough information to decide whether "C" or "D" is the best answer (even if the fact that "D" is a C 1 path makes a big point for it to be more plausible than "C").
The best way to remove this issue is to substitute the word "quickest" with "shortest".
By the way, I noticed that also many car-gps-system make the same assumption and often they tent to prefer a route that is shorter but it has a lot of discontinue changes of directions with respect to a better route maybe a little longer but with less changes
I remember that I provided a solution to this question which I felt myself quite satisfied with it. Unfortunately, it was deleted I think. This is not a very good culture without notification to me.
One needs to know how fast you can travel through water with respect to your speed on land. If your speed on land is x and your speed in water is 0.00001x it is obvious that D is the correct answer.
https://youtu.be/skvnj67YGmw
Before I begin I want to point your attention towards Fermat's Principle of Light: The path taken between two points by a ray of light is the path that can be traversed in the least time. Consider the Brilli as pt.2 and yourself as point 1. Now the beach and the sea represent two media. If light were to travel from pt. 1 to pt. 2 and through these two media , it would surely take the least time. Now we all know that the path taken by light is similar to only one option resembling the options.
The analogy is nice; however, the spoiler is that the lifeguard may have variable speed within each medium, whereas light has a fixed (apparent) speed within each media, and speed c in a vacuum.
Obviously, we want to spend less time in water, so option B is obviously worse than option C, so C can't be the answer. Likewise, option A is worse than option C. Option D looks like it enters the water at the same point as option C, but it is a curve. Since the shortest distance between two points is a straight line, option D is unnecessarily long. Thus, the answer must be C
answer is c. It is quite similar to law of refraction where a light ray bent toward normal when entering in dense(water) medium where velocity is less in compare with rare(sand) medium.
D does not enter at the same point as C
Surely this depends on where (on option D) you enter the water AND the relative speeds in water and on the sand. Minimising the distance in Water (slow) would be offset by the longer (curve) on the sand IF the speed on sand was significantly greater that the water speed.
If C and D enter the water at the same point, then I agree C is quicker... but the image is unclear.
Typo? Should "C can't be the answer" be "B can't be the answer." C, after all, is the answer
Not enough imformation to answer. We need to know how much faster on land than in water. If the difference is continually reduced then at some point option A will be the fastest.
The runners momentum entering the water is greatest at A. At C you lose some energy as you change direction.
I don't know the answer.
My Labrador Retriever always gets this one right. In a field trial she is supposed to do A (straight line across land and water), but she is too smart for that and does C (the fastest way)
I wonder what fraction of Brilliant problems can be solved this way?
wat) that wasint my full explanation (btw) it's not equal to d. but it is equaled to a. with x^5. we make this y = b t w × 3.
We can simply think it as an light particle refracting between the two surfaces.Then, answer is either B or C.Since,speed in sand is greater,I will move more distance on the sand.Hence,C is the correct answer.
Like light propagates in the medium,quentions like these all obey Snell law
Sin i / Sin r = v1/ v2. We should do as light does.
Two words 'Snell's law ' On finding the answer to this solution you actually derive Snell's law
Consider the situation for light. You will then apply snell's law. That would be due to different refractive indices. Similarly, here instead of refractive index, we compare speed. The speed in water will be lesser than in sand. The rest is self explanatory. Correct answer being C
When the difference of speeds is maximal in favor of running, the lifeguard will run to the point closest to tbe ant, to minimize tbe time of swimming. There is no solution shown for this, though this can be seen as a limit of C.
In the opposife situation, when swimming is faster tban running as if using a boat, the lifeguard will run straight to tbe shore to minimize the time of running - case B. If the speeds are equal, the the guard will run and swim in a continuous straight line - case A.
Knowing the ratio between the speeds we could calculate the angle of C.
C is the solution.
The question isn't complete. It doesn't give how much faster it is to travel in the sand. Imagine if traveling in the sand increases your speed by an infinitesimal or extremely small amount. You would want to take the straight line. Therefore, w/o specific details on how drastically the sand increases your speed the answer could be either A or C. I'm not positive about this so if you agree or disagree please let me know
The higher the differe .ca between the speeds, the closer to 90 degrees will be the angle of swimming. At an extreme, when speed of running is many times higher than speed of swimming, the lifeguard runs to the point right in front of the drowning ant and swims minimal distance.
Its the same that happens when light refracts. The question is not asking the minimum distance, it is asking the minimum time. So, when light refracts, then also, it does not take the distance with the minimum length but it takes the distance that takes least time to travel.
We have two medium sand and water. We can move fast on sand than water. So we should need to cover maximum and shortcut distance from sand than after left part from water.
Since you travel fastest over sand, you want to optimize distance run on sand instead of water. C has the longest stretch of sand to run over. Thus, it is the fastest.
You can't solve this without knowing exactly how fast you travel. For instance, what if you travel 99% as fast on water? Then C is a waste of time.
Log in to reply
Wow, I had the exact same idea, but I couldn't write a solution as I didn't get the correct answer. Without knowing the ratio between the two different velocities one cannot know whether A or C or D is the fastest. However, we do know the answer will always be analogous to C: when both velocities are equal, C would just make up two straight lines just like A, but this is the only case in which A also applies and also the case that falls just outside of the boundary of what velocities are accepted. Then when going towards the other impossible case that falls just outside our other boundary condition, we'll end up with the line through the water simply being the shortest distance between Brilli and the sand. Thus we conclude the inserted angle for C might be wrong as we do not know the ratios between the two velocities, but the lines drawn to illustrate the shortest time-path to Brilli from where You are, will always be analogous to C, and never to any of the other choices given to us.
Since we don't know how much time we save on sand versus water -- values were not given to us -- we probably want to run on the sand until we are at the shore point where swimming directly to Brilli is a 90 degree angle to the beach. That way you cover the shortest distance possible in the water, spending the most time on the sand. However, this is not one of the multiple choices, so C is the best answer. Presumably, this is because at some point increasing the distance covered on sand outweighs spending a little more time in the water.
Log in to reply
So D should be the answer Richard. As shortest distance is the perpindicular distance which is almost clearly shown in D
Log in to reply
The big problem with D is that the path does not take you in a straight line. Thus, you waste too much time travelling in a curved path. The increased distance would likely make D the wrong path to take. If the lines were straight instead of curved, then D would be very competitive with C, and then it would be difficult to choose the better path without knowing the speed values of swimming versus running on sand.
Log in to reply
@Richard Levine – The time lost walking on sand, as you are saying in option D is less than the time lost while swimming on an angular path in option C. In addition to it, speed in sand> speed in water. So D should be more apt anyhow
Log in to reply
@Arpit Kothari – I agree with you. A, B, and C options are same since no distance of the meeting points are given. Only D option can create a difference than others. If question states the distances we can compare the options...
@Richard Levine – Under no circumstances, D is better than other options.
from the information given it is sufficient to judge that the best possible path (from the given options) is C.if given the ratio one can determine the exact path.we can easily formulate the problem mathematically and then differentiate the resulting expression to find the point on the boundary which is sufficient enough to reveal the path.
On the base fact that C water distance is < D water distance. And you cannot draw a conclusion based on a possibly inaccurate depiction of a hypothetical situation.
Agree that C has longest sprint across sand to get the lifeguard the closest with shortest distance through water. My only complaint is that the lettering of the four drawings is counter-intuitive, moving down to B instead of left to right, causing me to mark the wrong letter in the solution!
We need to optimize the distance traveled by splitting up the route into two parts: sand and water. Since it's less efficient to travel in water, it makes sense to travel less on it. C is the quickest path because it is almost a straight line while keeping the water part short.