Save the Civilians!
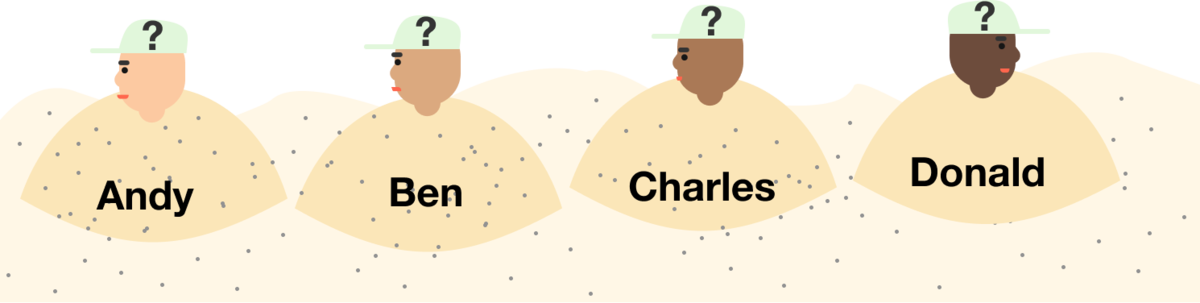
While at the beach, Ted buried his friends in the sand with only their heads sticking out, as indicated in the image. Charles could see Ben and Andy only, Ben could see Andy only, and Andy and Donald couldn't see anyone.
Ted showed them 4 caps--2 black, 2 white. Ted then randomly placed these 4 caps on their heads, without showing them the color of their own cap. Without any communication, the 4 friends had to guess the color of the cap on their own head and whisper it into Ted's ear.
Find all of the people with the highest probability of guessing correctly.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@jaiveer shekhawat Nice question! Before doing the math, one would at first anticipate that Charles, having more information, would alone have the best chances of surviving, so it was a surprise to find out that Ben had the same chances. To this end, it might be better to have "Charles" alone as one of the answer options, since this is the one many people would first assume is correct. If you can't make the change I think I can as a moderator, or Staff could as well.
Feel free to modify it as per your wish!
Log in to reply
Ok, To be on the safe side I'll first check with staff if this is something I can do as a moderator.
@Calvin Lin Would it be possible to add "Charles" as one of the answer options, or change one of the existing (incorrect) options to "Charles"? My reasons for this request are outlined in my comment below. I suspect that while it appears that I can technically make a change, this is something that only Staff is allowed to do. Thanks.
Log in to reply
Thanks. I've added Charles as an additional option, and reordered the options.
This looks like an interesting question :)
Log in to reply
@Calvin Lin – Great! Thanks for doing that. :)
It might be good to write out the erroneous reasoning for "Charles only" (for which I fell).
Charles either (50%) sees two equal colors in front of him, in which case he knows for sure (100%) his own color is the opposite. Or (50%) he sees two different colors, in which case Donald and he have opposite colors as well, and he has a 50% chance of guessing correctly. Altogether that gives him a 0 . 5 × 1 + 0 . 5 × 0 . 5 = 7 5 % probability of guessing right, which is better than Ben's 2/3.
However, as pointed out, the probabilities of him seeing two equals or two opposites are not 50-50, but rather 1/3-2/3. Very nice (and counterintuitive) indeed. So, Charles' probability is in fact 3 1 × 1 + 3 2 × 0 . 5 = 2 / 3 , equal to Ben's.
Log in to reply
I chose "Charles only" too. If Charles chose to ignore what hat Andy is wearing, he would still have the same probability of being correct.
Seeing two hats can help Charles be certain of what hat he is wearing (when he sees two same colors) , and can sometimes confuse him (when he sees two different colors).
I thought that all the hats were distinct. Could you please add a statement saying that "Hats are all identical , except colour." Or maybe like "Hats of same colour are identical."
Log in to reply
The calculation for Ben would be the same whether the hats are distinct, (except for colour), or not.
For Charlie, if the hats were distinct, then there would be a sample space of 2 4 hat arrangements. In 8 of these Andy and Ben would have the same colour hat, and in the other 16 they would have different coloured hats. The probability calculation would then be
2 4 8 × 1 + 2 4 1 6 × 2 1 = 2 4 1 6 = 3 2 .
Since the result is the same, I don't think that it is necessary to make any edits to the problem statement.
Given the choice in whos position would you place yourself in?
Log in to reply
I have nightmares about being buried in sand. I would have avoided ever associating with Ted; he seems to be a sociopath. :p
But seriously, before doing the math I would have chosen Charles' position without hesitation, so it was a surprise to find that Ben's position offered the same chances.
Despite all these comments; would you rather want to be in Charles position or Ben's?
Log in to reply
Before doing the math I would have chosen Charles' position without hesitation, so it was a surprise to find that Ben had the same odds as Charles did. To be honest I wouldn't want to be buried in sand at all, so I would avoid Ted completely and skip going to the beach. :p
Here's a non-numerical way of seeing that Ben and Charles must have the same probability of guessing correctly: Clearly Charles has the option of using the same strategy that Ben would use (i.e. guessing the color that Andy is not wearing). But can he improve on this strategy, i.e. should he change his guess based on what color Ben is wearing?
If Ben is wearing the same color as Andy, then Charles should definitely not change his guess. If Ben is not wearing the same color as Andy, then either guess is equally good. Therefore, Ben's strategy is optimal for Charles as well.
Neat problem. Try out this variation: 3 black hats, 1 white hat . Very counterintuitive results! This has me thinking about how the probability of guessing correctly evolves as you see additional hats.
P(n) = probability of guessing correctly after seeing n hats
Apparently, the function P(n) is not strictly increasing. It can be constant: P(n+1) = P(n) is possible.
Can you post that version of the problem?
That is really interesting!
i don't think it's that surprising. No matter what person you are, and in what situation you are, guessing your hat is black is the best strategy. Information doesn't matter.
The problem can be solved very simply thinking that: if Andy and Ben have the same colour, Charles will immediately answer the opposite colour: the probability A and B have the same cap is 1/2. Otherwise, if they have different kind of cap, Charles will not be able to answer, but Ben can notice that if Charles doesn't answer, it means that his own cap is different from Andy's, so he will answer the opposite colour. He also has P=1/2. So Ben and Charles have the same chances to answer correctly.
Moderator note:
As pointed out by Janilson, this solution is flawed because it assumes that there is communication, and furthermore that Ben knows why Charles made his guess.
In addition, the probability that Andy and Ben have the same color hat is 1/3, not 1/2.
They aren't able to hear the other answers (they will whisper it into Ted's ear) so Ben doesn't have the same level of Charles' probability... Charle can take the flawless guess if the 2 caps in front of him are blacks/whites
Log in to reply
Thanks for pointing out the errors with this solution. I've added a note so that others are made aware of it.
It is somewhat surprising that even though Charles seemingly has more information, it isn't helpful enough to improve his overall probability of guessing.
In cases where Andy and Ben have the same color, Charles knows for certain what he has. However, when Andy and Ben have different colors (which is twice as likely to happen), then Charles only has a 50-50 chance of being correct.
Both Andy and Donald, not having any information about about anybody's hat colour, have a 2 1 probability of guessing correctly.
Ben, seeing Andy's hat colour, knows that 2 of the remaining 3 hats will be of the colour opposite that of Andy's. So by choosing this opposite colour he will have a 3 2 probability of being correct.
Charles has more information, seeing both Andy's and Ben's hats. Now in general there are 2 ! × 2 ! 4 ! = 6 possible hat colour arrangements. In 2 of these both Andy and Ben will have the same colour of hat, in which case Charles will be certain of his own hat colour. In the other 4 possible arrangements Andy and Ben will have different coloured hats, in which case Charles would have only a 2 1 probability of guessing his own hat colour correctly. Thus the overall probability that he will choose correctly is
6 2 × 1 + 6 4 × 2 1 = 3 1 + 3 1 = 3 2 ,
which is the same as Ben's chances. So while Charles has more information than Ben, his chances of surviving are the same as Ben's, both of which exceeds the chances of Andy and Donald.
Thus the answer is Ben and Charles .