Say My Name
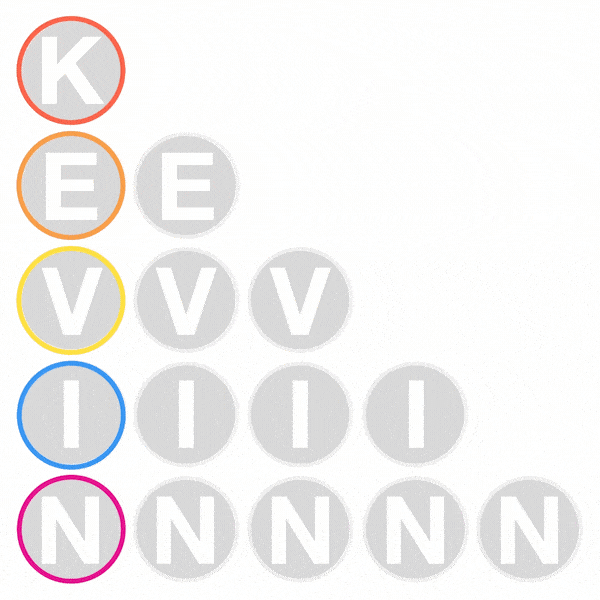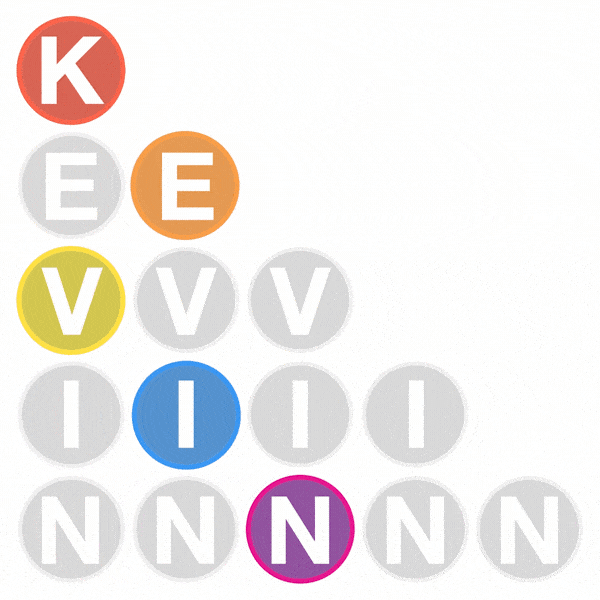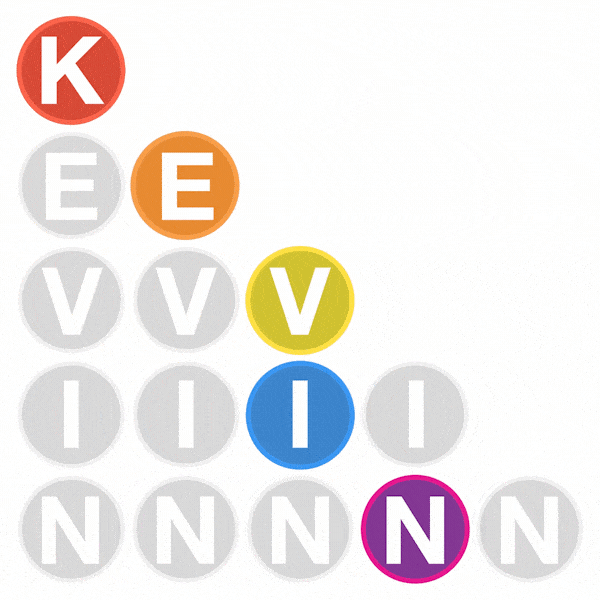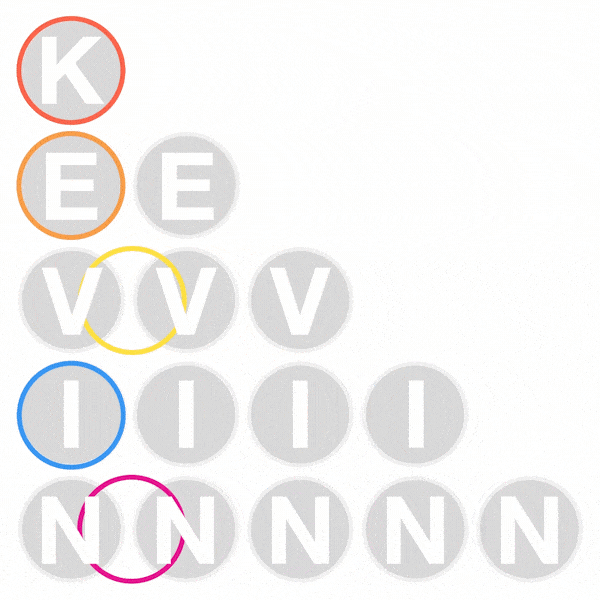
You are given 15 letters above with which you can write my name KEVIN.
Suppose that, each time you go down one row, you have 3 choices: go straight down, or go diagonally one to the left, or go diagonally one to the right.
Then, how many ways are there to spell out KEVIN?
Bonus: Can you generalize to n rows?
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
There's a strong resemblance between this solution and the common method of drawing Pascal's Triangle , which is having each number sum the values to the immediate upper left and upper right of it.
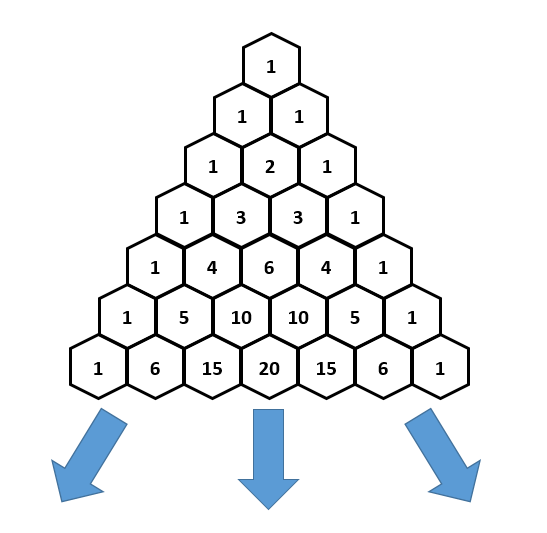
The sequence for the number of ways to spell out n letters is:
1 , 2 , 5 , 1 3 , 3 5 , 9 6 , …
If we only looked at the first few terms, we might make wrong guesses about the pattern. The starting looks like some Fibonacci numbers, of even of the form 2 n + 3 n . Unfortunately, the pattern does not hold, and the sequence is more complicated than that. The closed form is:
Consider ( 1 + x + x 2 ) n − 1 . Take the coefficient of x n − 1 plus the coefficient of x n .
Unfortunately, I do not know of a simple proof to demonstrate this. If you are interested, you can read the literature on such problems.
Great job!
What tool do you use to create this graphics?
Log in to reply
Thankyou!:)
I used Adobe Fireworks to make squares and add text. For shapes I would normally use Figma, which is free, cloud-based software:)
True, the triangle comes up a lot in discrete maths!
the nth term seems to follow the integer sequence OEIS A000107
I think that indeed, for n letters the formula is 2^(n-2)+3^(n-2). I’ll try to come back with larger explanations.
1
1 1
2 2 1
4 5 3 1
9 12 9 4 1
9+12+9+4+1=35
No need to say what I did ;)
Can you explain in words what you did?
Do you see a pattern? Can you guess why that's the case?
Log in to reply
There is one possible way to get to the K. Then, there is 1 way to get to the first E and one to get to the second E. After that, there are 0+1+1 ways to get to the first V, 1+1+0 to the second, 1+0+0 to the third... every cell is just adding the top number, the top right number and the top left number. In the end, add all the numbers of the last row to get the result.
Log in to reply
If you list out the number of ways for each row, you will get 1, 2, 5, 13, 35, ...
Do you recognize this?
Log in to reply
@Chung Kevin – At first I thought that these are the alternate terms of Fibonnaci sequence having the same parity order (as shown below):
0 , 1 , 1 , 2 , 3 , 5 , 8 , 1 3 , 2 1 , 3 4 , ⋯
But then the number 35 popped up in your sequence instead of 34, so I realized this was some other sequence. Can you tell me which sequence do you have in your mind?
Log in to reply
@Tapas Mazumdar – That's a good observation, that the 5th term doesn't fit into the Fibonacci sequence, much as we want it to. This isn't a "well known sequence", but it's been studied before.
This is a slightly complicated sequence to deal. I was using recurrence relations to work with it.
Log in to reply
@Chung Kevin – Did you get any recursive relations for this?
@Chung Kevin – I've noticed one pattern between successive numbers that each term f(n+1)=3×f (n)-g(n)
Here g(n) is identical to the number of paths from the first point on the base row to the top of the n-triangle.
I suspect this is more a consequence of the general solution than a route to solving it.
Log in to reply
@Malcolm Rich – Right, you can get that by looking at the generating function.
If you let f n ( x ) be the generating function for the number of ways to get to the nth row, where the coefficient of x m corresponds to getting to the (m+1) th column, then (because only the first column is prevented from going left), we have
f n + 1 ( x ) = ( x 1 + 1 + x ) × ( f n ( x ) − f n ( 0 ) ) + ( 1 + x ) f n ( 0 )
Letting x = 1 to find the sum of the coefficients, we get f n + 1 ( 1 ) = 3 f n ( 1 ) − f n ( 0 ) , where f n ( 0 ) coressponds to your g ( n ) .
Log in to reply
@Calvin Lin – A005773 Number of directed animals of size n (or directed n-ominoes in standard position).
Found it here
In your animation the letter "N" in the last row moves two to the right when first forming an outmost diagonal "Kevin". Is this allowed?
Log in to reply
Can you be more explicit? E.g take a screenshot to state which frame you are referring to, or like the first frame is (1, 1, 1, 1, 1) and the second frame is (1, 2, 1, 1, 2).
I looked at the individual frames, and they all satisfy the condition of "go straight down, or go diagonally one to the left, or go diagonally one to the right."
Note that the problem isn't about "comparing 2 different sequences (IE animation) it moves two to the right",
Log in to reply
@Calvin Lin – From the 4th frame (1,2,2,3,3) it goes to the 5th frame (1,2,3,4,5). So this is allowed?
Log in to reply
@Guy Fox – Note that the problem isn't about "comparing 2 different sequences (IE animation) it moves two to the right". So saying "from 4th to 5th" is out of the scope of the question.
The 4th frame (1, 2, 2, 3, 3) satisfies the condition of "go straight down, or go diagonally one to the left, or go diagonally one to the right."
The 5th frame (1, 2, 3, 4, 5) satisfies the condition of "go straight down, or go diagonally one to the left, or go diagonally one to the right."
Hence, both the 4th and the 5th frame are allowed.
Does this clarify the problem?
Great! Time to generalize to n rows ;)
I think the answer is simpler if the paths are reversed
Realize that the sum of the terms of the row n is the sum of the terms of the row n − 1 minus the first term of the row n − 1 (extremely easy to prove). Therefore, it is sufficient to find the first element of every row to find the sum of the elements of every row.
In 3rd row why its 221 not 222, we can reach to last element in 3rd line by 2 ways
Log in to reply
Could you describe which two ways did you get to reach the last element in the third line? I am getting only one way: K --> rightmost E --> rightmost V.
Log in to reply
I got it now, the rule says: "go diagonally one to the left, or go diagonally one to the right" its because of that we cant move directly from leftmost 1 in second row to rightmost 1 in 3rd row, because of the rule defined above.
Reverse all routes and see how many ways of climbing the pyramid from N to K.
First row (1,1,1,1,1) Second row (2,3,3,3) Third row (5,8,9) Fourth row (13,22) Answer is the Final row = 35
This leads to my fledgling ideas for the general solution. With a symmetric triangle, the value at the top of the triangle is 3^n. This may not be the simplest way of identifying the answer but it's worth looking at.
Log in to reply
Is that so? But for instance, in this particular case, it is not 3^n
Log in to reply
If we extend the triangle to the left so that every step down the triangle has three paths - in this case there would be 9 N's on the bottom row - then each point on the (i+1)th layer of this triangle would have have 3^i routes from the bottom row.
Our non-symmetric case differs for two reasons. Firstly, the (n-1) size triangle to the left is missing so all paths starting here are absent. Second, we cannot take any path starting in our n size triangle that would have passed through this smaller triangle.
Log in to reply
@Malcolm Rich – That's a great observation! Very similar to how I was thinking about it. It's slightly troublesome to account for the "missing paths" though.
General solution would be 3^(n-2) + 2^(n-2)
Log in to reply
General solution would be 3^(n-2) + 2^(n-2)
Are you basing that on the fact that it works for n=2,3,4,5?
I did the same thing, and then made a mistake adding up 22 and 13 without using a calculator :-(
This was the simplest way for me. I found only at twice, because i made the same error of addition like Kris H. (me too ashamed :( )
35
13 - 22
5 - 8 - 9
2 -3 -3 -3
1 -1 -1-1 -1
Calculations are from lower row to the top row
35
13 - 22
5 - 8 - 9 ----> eg 5 -- from this node you can access either node(2) or(3)
-----------------> 9 -- this node can access 3 nodes each (3)
2 -3 -3 -3 --- > number of ways to move from this row to the lower row.
1 -1 -1-1-1 ------> terminal leaves
Hmmm, I don't understand your solution. What does all these numbers represent?
NOTE : The sum of the number of ways of getting to each letter by following the above mentioned rule, gives us the total number of writing Kevin's name ! Now note the number of ways of getting to each Letter, we observe it as below,
1
2 1
3 2 1
4 3 2 1
5 4 3 2 1
Adding all these gives, 35 .
Using this we can easily generalise it for n terms. Sumate the summations of first n, n-1,n-2,n-3... @Chung Kevin please go through the approach and let me know.
Log in to reply
That's the recursive approach to the problem, where we calculate all of the intermediate steps.
Is there a closed form for the answer?
Log in to reply
(3^n)+(2^n)
Log in to reply
@Nirmal Kumar – Replace n with n-2 :)
Log in to reply
@Nirmal Kumar – 1st term is 5/6 not one, works for the others up to 35
@Nirmal Kumar – Great guess! Unfortunately, the next term is 96, which doesn't fit this pattern.
But this solution only happens to give the correct result for a 5 character name, but does not work for a general solution. Consider a 2 letter name in a triangle as in the above problem. This solution would indicate 4 possible paths, where there are in fact, only 2.
I don't understand your solution. How do you compute the numbers?
@Christopher Boo notice the number of ways you can reach a particular letter following the given rules. For Eg the second N from the right end- can be approached diagonally right or straight down ( I.e 2 ways ) from the I's. Following the same logic we can observe the pattern.
@Christopher Boo Please do excuse my solution as I couldnt put up a perfect solution with legit steps due to my hectic schedule . Please do let me know if you note any errors to the approach.Thank you.
@Chung Kevin I think a closed form can be build. But I think there are many flaws and gaps to fill in ,to the approach.
@Peter Freese thank you. Yeah I noticed it. This is not fitting and generalised. I shall look onto generalising it soon after I'm free and I think there are a few miscalculations in the solution as well. @Chung Kevin do you have a generalised solution?
What is dp?
its short for dynamic programming a.k.a memoization of reccurence
But obviously I didnt do any programming for this small state and base cases
Let's view the letters in a grid: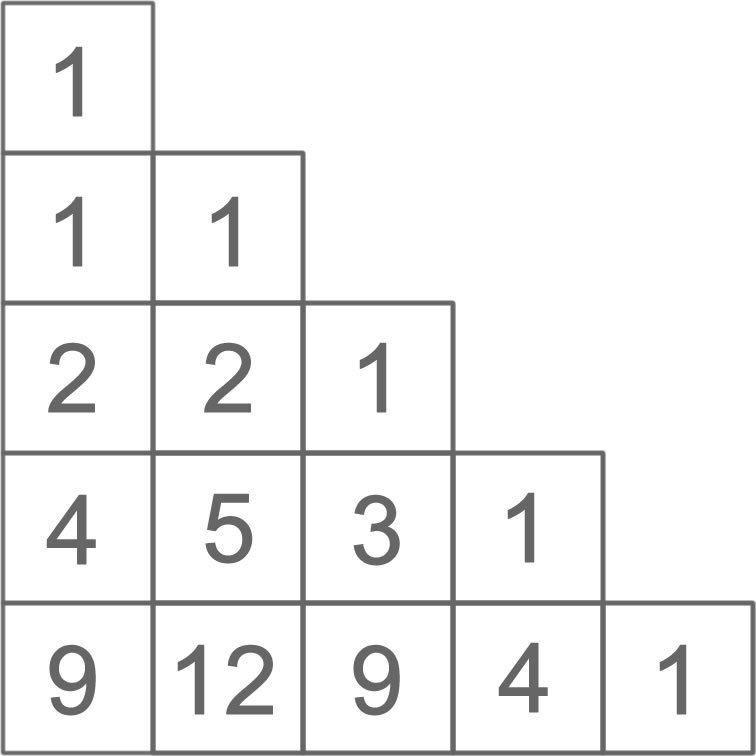
The numbers represent the number of ways to get to a particular square, starting in the left-most upper square.
There is one way to start in the top left, and that is by starting in the top left!
There is one way to reach either of the tiles on the row below. In general, to determine the number of ways that we can reach a tile, we sum the numbers in the tiles above that could potentially lead to that tile.
For example, you could reach the number 5 tile by coming from either of the number 2 tiles above or the number 1 tile above. This gives 2 + 2 + 1 = 5 combinations for reaching the number 5 tile.
But for tiles in the diagonal, they can only be reached by coming from the tile directly up and to the left, and so the number of paths that lead to these diagonal edge pieces is always 1.
The total number of combinations is the sum of the number of ways of reaching the bottom row, which in this case is 9 + 1 2 + 9 + 4 + 1 = 3 5 .