Scattering protons and positrons
Two protons and two positrons form a square as shown in the figure. All the particles are initially at rest. Due to Coulomb's repulsion, the particles fly off to infinity. Determine the ratio
v
e
v
p
where
v
p
and
v
e
are the final velocities of the protons and positrons, respectively. Note that the positron, being electron's antiparticle, has the same mass as the electron and opposite charge
(
q
=
+
1
.
6
×
1
0
−
1
9
C
)
.
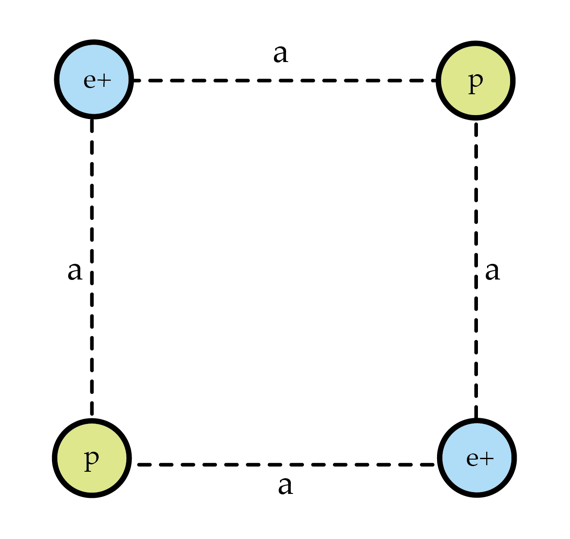
Details and assumptions
- m e m p = 1 8 3 6
- Hint: since the protons are so much heavier, you can do this without having to solve momentum conservation. Think about which particles fly away first...
The answer is 0.009.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I am still confused.. when protons start flying away, their speed is going to be v p but don't we need to be concerned about asymptotic speed? Same for positrons also..
Log in to reply
I am not sure what you mean by 'asymptotic speed'. I googled it, but found no appropriate results (apparently it is out of reach of an average high school student like me). Could you please clarify?
Log in to reply
Speed when the particles "reach" infinity..
Log in to reply
@Snehal Shekatkar – Didn't we determine the ratios of the asymptotic speeds then?
If you are confused about the part when I wrote that the electrostatic energy experienced by each of the positrons is m e v e 2 / 2 , note that since the protons are much heavier than the positrons, the acceleration of the positrons will be much higher than that of the protons. This way, we can consider an instant when the protons are at their places, but the positrons flew away to (almost) infinity.
Log in to reply
@Sreejato Bhattacharya – Yes but protons have not yet reached to infinity yet.. so their speeds may change after some time.. They are acting some force on each other since they have not reached infinity and so corresponding speeds should change I think.. That is where I got stuck while solving this problem and couldn't proceed..
Log in to reply
@Snehal Shekatkar – Since they are very far away from each other, we are neglecting their mutual forces (this is an assumption that must be made for the sake of simplicity).
Let's use energy method to solve this problem. First consider the initial potential energy. To find the initial potential energy we set up the system by moving the charges one by one to their position. The first particle takes no energy to move from infinity to its current position since there is no other charge. The next particle has to move against the first charge from infinity giving.
V = a k q q
where k is coulomb's constant, and V is the potential.
The next particle has two terms since there are two charges where one is a distance a away and the other is a distance 2 a away.
V 2 = a k q q + 2 a k q q
The last particle has three terms since there are three charges where two are at a distance a and the other is at a distance 2 a
V 3 = a k q q + a k q q + 2 a k q q
Combining all the potentials to get the total potential gives
V t o t a l = a ( 4 + 2 ) k q q
Once the particles return to infinity, all the potential energy will be kinetic energy. This gives the following equation.
a ( 4 + 2 ) k q q = 2 1 m p v p 2 + 2 1 m p v p 2 + 2 1 m e v e 2 + 2 1 m e v e 2
or simplified
a ( 4 + 2 ) k q q = m p v p 2 + m e v e 2
Now, because the positrons are so much lighter than the protons, they will reach infinity before the protons have moved substantially. This means we can relate the potential of just the protons to the kinetic energy of just the protons. The potential is simply
V = 2 a k q q
So the energy equation is
2 a k q q = 2 1 m p v p 2 + 2 1 m p v p 2
or
2 a k q q = m p v p 2
Now we have two equations. Divide the first equation by the second which gives you
2 ( 4 + 2 ) = 1 + m p v p 2 m e v e 2
After algebra this equation becomes
( 4 2 + 1 ) m e m p = v p v e
Since we know m e m p , all the values on the left hand side of the equation are known. Plugging in those values and then inverting both sides gives
v e v p = . 0 0 9 0 5
Let's use energy method to solve this problem. First consider the initial potential energy. To find the initial potential energy we set up the system by moving the charges one by one to their position. The first particle takes no energy to move from infinity to its current position since there is no other charge. The next particle has to move against the first charge from infinity giving. where is coulomb's constant, and is the potential. The next particle has two terms since there are two charges where one is a distance away and the other is a distance away. The last particle has three terms since there are three charges where two are at a distance and the other is at a distance Combining all the potentials to get the total potential gives Once the particles return to infinity, all the potential energy will be kinetic energy. This gives the following equation. or simplified Now, because the positrons are so much lighter than the protons, they will reach infinity before the protons have moved substantially. This means we can relate the potential of just the protons to the kinetic energy of just the protons. The potential is simply So the energy equation is or Now we have two equations. Divide the first equation by the second which gives you After algebra this equation becomes Since we know , all the values on the left hand side of the equation are known. Plugging in those values and then inverting both sides gives
Let's try to find the total electrostatic energy of the system before the particles start flying out. Notice that the length of the diagonal of the square is given by 2 a .
All of the particles experience an electrostatic potential of magnitude a k e 2 from each of the particles adjacent to it, and an electrostatic potential of magnitude a 2 k e 2 from the particle diagonally opposite to it. Summing them up, we find out that the total electrostatic energy of the system is E i = a 4 k e 2 + 2 a 2 k e 2
Now, since the protons are much heavier than the positrons (this was hinted in the second clarification), the positrons fly away much faster than the protons. Consider a moment of time when the positrons are flying away, but the protons are still there. The electrostatic potential experienced by each of the positrons is given by 2 m e v e 2 . Summing them up, we find out that the total electrostatic energy in the system is E f = 2 × 2 m e v e 2 + 2 a k e 2 From conservation of energy, we know that E i = E f ⟹ m e v e 2 + 2 a k e 2 = a 4 k e 2 + 2 a 2 k e 2 Now the protons also start flying away, with velocity v p . In this case, we obtain m p v p 2 = 2 a k e 2 A little bit of manipulating these equations gives v e v p = 1 + 4 2 1 m p m e Plugging the values from the question gives v e v p ≈ 0 . 0 0 9 .