The Hydra
 Out in the desolate clutches of the forsaken seas where the winds and rains know no sleep, rests a scroll upon which are written secrets that might drive one to insanity from merely reading them. Great and terrible knowledge, necessary for forwarding in a new age of civilization, yet dangerous in its ability to destroy. Our hero has gone through many trials to find this rock, and suffered many things for his journey, but now he is here, and but one obstacle remains.
Out in the desolate clutches of the forsaken seas where the winds and rains know no sleep, rests a scroll upon which are written secrets that might drive one to insanity from merely reading them. Great and terrible knowledge, necessary for forwarding in a new age of civilization, yet dangerous in its ability to destroy. Our hero has gone through many trials to find this rock, and suffered many things for his journey, but now he is here, and but one obstacle remains.
Before the hero stands a mythological Hydra . It begins, graciously enough, with but one head. The hero has but one way to attack the beast - slice off its head.
But this is no sure method, for, with equal probabilities, a severed head of the Hydra may either wither into nothing... or sprout again as three, new, different heads. When such an event happens, the hero has no choice but to slice again at another head, each exactly like all the others - each head having the same chance of either withering away, or sprouting into three new heads instead.
Let P be the probability that the hero defeats the Hydra - that is, he succeeds in slaying every single head, and the last head he slays does not regrow. The alternative option being that he spends an eternity in battle with the Hydra, never defeating all of its heads.
What is ⌊ 1 0 1 0 P ⌋ ?
Image Credit: http://powerlisting.wikia.com/wiki/Hydra Physiology?file=Hydra vs_Monk.jpg
The answer is 6180339887.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Just a note that the process is equivalent to a branching process with μ = 3 / 2 > 1 and we merely require its extinction probability p . Hence, as given in the wiki article, (or more precisely, here ), p is the unique solution in the interval [ 0 , 1 ) of the equation p = h ( p ) where h ( ⋅ ) is the moment generating function of the offspring distribution, which, in this case is simply h ( p ) = 2 1 + 2 1 p 3
Log in to reply
It's also equivalent to a random-walk problem, where you start at h = 1 , head left 1 step with probability 1 / 2 (head dies, -1 head), and head right 2 steps with probability 1 / 2 (head splits, -1 head + 3 heads), and you want to know the probability of ever reaching h = 0 .
Log in to reply
Not really ! Say you are at h = 3 at step 2 (i.e. you cut off the head at the first step and the hydra gives rise to three additional heads). Then at step 3, you could be either at h = 0 (you cut off all three and none of them reproduces) or h = 3 (you cut off all three and only one reproduces), or h = 6 (you cut off all three and two of them reproduce), or h = 9 (you cut off all three and all of them reproduce). Hence your transition probability is dependent on the current state, which is NOT allowable in random walks.
Log in to reply
@Abhishek Sinha – That's if you interpret each step as a branching generation, where all of the heads either die or multiply simultaneously. The random walk interpretation is valid if you interpret each step as a single attack made by the hero - only one head either dies or multiplies, and the rest simply idle, unchanged.
Log in to reply
@Daniel Ploch – Can you write down a detailed solution with this interpretation, describing the state space and transition probabilities of the random walk? It will be interesting to see that.
Log in to reply
@Abhishek Sinha – The formula is actually exactly the same as yours, but for different reasons. We model the number line as representing the number of existing, live Hydra heads, and each step in the walk is the outcome of attempting to slay a single head.
As per the problem, we add − 1 to our current position with probability 2 1 , and we add 2 to our position also with probability 2 1 , regardless of where we are located. Then, consider the constant probability r that, starting from point h , we eventually reach h − 1 , which is constant for all h due to statelessness.
We can reach h − 1 immediately from h with probability 2 1 . Otherwise, we go to h + 2 , and then we must eventually go back one unit three times.
So:
r = 2 1 + 2 1 r 3
And this yields the same numerical answer.
That's exactly how I solved this, bounding the heads to 10000 (that is, I assume > 10000 heads == 0 probability of winning) is more than enough ...
Running it with 1000 iterations had all the P(1) thru P(10000) converges to stable values. We of course will need to just get P(1).
great answer to a great problem, with a great picture
Nice question bro, it's still going at Level 5 400 points !!
Simply the most beautiful Combinatorics problem on Brilliant I've seen till now. Took me almost an hour to do. ( Yes I am slow)
Neat problem, but just curious, does the golden ratio apply for all n (n being the number of heads that arise from one head)
Log in to reply
I think not. For 'P' being the probability of killing the Hydra, we said that P=0.5+0.5P^3 , here we have P^3 because the 'first head' can create 3 more scenarios that are equivalent to P . If we had a different number of heads, such as 5, then we would not get a cubic but an equation to the power of the number of heads generated, in this case P=0.5+0.5P^5. In the case that 5 heads were generated we would get (p-1)(p^4+p^3+p^2+p-1)=0, again we can discount P=1, so the 'true' probability solution is one of the roots to the quartic. I think it should be clear that this will have a different number of roots that take different values (highly likely all different) to the quadratic we get for the case where 3 heads are generated. According to wolfram-alpha in the case where the number of heads is 5, the probability would be approx 0.51879 that makes sense when you think that the more heads are generated, the less likely (relatively speaking) that the hero is to succeed. Regardless, the key point is that by changing the number of heads created in a failed strike, the probability of success would seem to change and thus it is only due to the formulation of the problem that 3 heads were produced and each outcome happened half the time that we found the golden ratio came into it.
At least that's the case from what I understand.
I hope I did not misinterpreted the problem but what is the definition of losing i.e. spends an eternity in battle with the Hydra? I answered 1 because I thought he could keep slicing the heads. Even if the number of heads reached incredibly high, there is still probability for him to win, it's only matter of time.
Say, if P = 0 . 6 1 8 is the probability that the hero defeats the Hydra, then the probability of the hero losing is P L = 0 . 3 8 2 . Again, will the hero loses?
Log in to reply
There are infinitely many ways for the hero to win and infinitely many ways for the hero to lose, because the number of heads can grow in different ways. This is different from problems in which the "losing forever" option is essentially always the same. So the probability may in fact not be 1.
Another way to think about losing is to consider the probability that at least n Hydra heads get attacked at some point, which we can call P ( n ) . So, P ( 1 ) = 1 , P ( 4 ) = 2 1 , P ( 7 ) = 2 1 ⋅ ( 1 − ( 2 1 ) 3 ) , and so on.
If you keep calculating these probabilities, you'll find that as n → ∞ , P ( n ) → 0 . 3 8 2 . . . , or precisely ( 1 − P ) . In other words, for any number of heads n , the probability that at least n heads will be attacked is at least 0 . 3 8 2 . . . , and so, equivalently, the probability that infinity heads will be attacked - the probability that the hero engages with the hydra for eternity - is effectively that number.
Log in to reply
wolfram alpha says this tends to around 0.43. Am I missing something? https://www.wolframalpha.com/input/?i=+%281-0.5%29%281-0.5%5E3%29%281-0.5%5E9%29%281-0.5%5E27%29%281-0.5%5E81%29...
Log in to reply
@A Former Brilliant Member – h t t p s : / / w w w . w o l f r a m a l p h a . c o m / i n p u t / ? i = + % 2 8 1 − 0 . 5 % 2 9 % 2 8 1 − 0 . 5 % 5 E 3 % 2 9 % 2 8 1 − 0 . 5 % 5 E 9 % 2 9 % 2 8 1 − 0 . 5 % 5 E 2 7 % 2 9 % 2 8 1 − 0 . 5 % 5 E 8 1 % 2 9 . . .
Why do we disregard 1 as solution? Why can't this be true? Although counter intuitive, is it possible that the hero always kills off the hydra in a finite number of strikes?
Log in to reply
Well, if P=1, this would mean every single strike the hero does will cut off a hydra's head which will not grow back. That goes against the whole problem which says NOT every head will grow back. If P=1, then the first head the hero strikes will wither, and that will be the end. Clearly our story can't end there :D
Log in to reply
I don't think this answer the question. If 2 heads would grow back instead of 3, then the probability would be P=1. Why is this not the case with 3 heads?
@Kalash Verma how did you solve Sharky Kesa's problem,'the Hydra'?Please post a solution.
Log in to reply
Similarly as the above given solution by Daniel Ploch.
Log in to reply
Did you solve this problem,and which method,the first one or the second one? @Kalash Verma
This is wrong. If the only two options are the hero eventually slays the Hydra, or the hero is eternally trapped in combat i.e. there is a 0% chance the Hydra will defeat the hero, then the only possible solution is that the hero defeats the Hydra. Even if we change the numbers and give a head a 1% chance to whither and 99% chance to sprout into 3, when taken to infinity, the chance of the hero getting a lucky streak eventually becomes 100%. Therefore P=1 and the correct answer is simply 10^10
Log in to reply
There still the option that the hero will battle the Hydra forever =)
I have an easy programming solution you can formulate a recursion
f( n ) = 0.5( f(n - 1 ) + f(n + 2) )
when f( 0 ) = 1
then we can assume that f( inf ) = 0
for purpose of this problem we can take f( 1000 ) = 0 then we can formulate a system of equation like
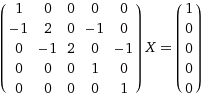
interesting solution
Bonus question:
What's the expected number of heads cut if you know you defeated the hydra?
I found 3 − 4 P 2 P = 1 + 5 3 5 ≃ 2 . 3 4 .
I got the same. Nice bonus question.
I solved it with:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
I also solved it with PHP to take advantage of longer execution time and more precision:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
Let p ( h ) be the probability that we slay the Hydra by killing exactly h heads, where, necessarily, h = 3 n + 1 for some n ∈ N . The probability of doing so is thus 2 − h , multiplied by the number of ways there are to kill precisely h heads.
For the sake of counting, let's assume the 'split' or 'die' fate of each head slain is predetermined ahead of time. The order of the hero's attacks do not matter. The number of ways to kill precisely h heads is thus the number of ways that a full ternary tree with h nodes can be structured, and that is:
T ( 3 n + 1 ) = 2 n + 1 ( n 3 n )
The probability that the Hydra is eventually slain is the sum of the probabilities that it is slain for all finite numbers of heads for which it may be slain. This summation converges, and it is:
P = ∑ n = 0 ∞ 2 3 n + 1 T ( 3 n + 1 )
Evaluating just a few dozen terms gives us the approximation:
P ≈ 0 . 6 1 8 0 3 3 9 8 8 7 4 9 8 9 4 8 4 . . .
⌊ 1 0 1 0 P ⌋ = 6 1 8 0 3 3 9 8 8 7
Alternatively, if you don't have a penchant for overthinking things like me, you might realize that P can be defined recursively - the probability of defeating 1 head is equal to the probability of defeating it immediately, plus the probability of it splitting, and then the other 3 heads being eventually defeated, each one being the same.
P = 2 1 + 2 1 P 3
Algebra yields:
P 3 − 2 P + 1 = 0
( P − 1 ) ( P 2 + P − 1 ) = 0
This yields three solutions:
P = − 2 5 + 1 or 2 5 − 1 or 1
The first is negative and can be discarded. The last solution, 1 , satisfies recursive definitions but is false as it conflicts with the convergent sum definition, which must also hold. Therefore only the intermediate solution, which is equal to ϕ − 1 , where ϕ is the Golden Ratio , is correct.
And ⌊ 1 0 1 0 ϕ − 1 ⌋ = 6 1 8 0 3 3 9 8 8 7