Seeu Sim's Leg

Calculus Level 5

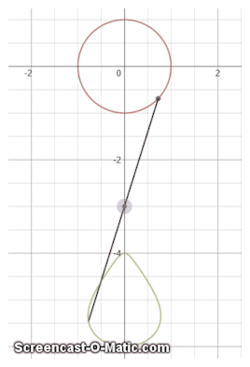
The above is a GIF showing the mechanism of a very simple but impractical leg. However, in maths, nothing is impractical.

It is known that the red colour circle above is of radius $1$ .

The coordinates of the purple point are $(0,-3)$ .

And the length of the black line (or leg) is $5$ .

The green egg-shaped shape traces the path of the bottom of the black leg.

Given that the area of the green egged-shaped shape is $A$ , find $\left\lfloor 1000A \right\rfloor.$

To be fair, you may use a computational method.

Try my Other Problems

The answer is 2170.

2 solutions

Lu Chee Ket
Feb 15, 2015

Sir, I'm quite happy to see a $\LaTeX$ solution from you $\ddot\smile$ ? And well explained too,sir . +1

A Former Brilliant Member - 6 years, 3 months ago

Did you find a non-numerical method to solve this question?

Lu Chee Ket - 6 years, 3 months ago

Sorry sir, even I used vectors .

A Former Brilliant Member - 6 years, 3 months ago

heres the simulation to play with.

Julian Poon - 6 years, 3 months ago

Counting pixels can be more accurate. Thanks for setting this question. Both x and d y in this integral ought to be varied, which is not usual. How do you solve this question?

Lu Chee Ket - 6 years, 3 months ago

Pretty much the same way

Julian Poon - 6 years, 3 months ago

@Julian Poon – I assume you mean that you have also applied numerical method. Thanks.

Lu Chee Ket - 6 years, 3 months ago

Incredible Mind
Feb 12, 2015

you have made my day,I used vectors hence typing is too hard but i can say the steps

1)take a random point on the circle that is vector A= (cos t,sin t)

2)consider point(0, -3) as vector B

3)take B-A to get the direction we need

4)now make B-A a unit vetor by dividing...by magnitude .Let this new vector be H

5)now multiply by 5 to this unit vector to get 5H

6)add this to A and get the pints on our required eyedrop that is A+5H

7)take x and y component separately and u will get

x= cos(t)-5cos(t)/(10+6sin(t))^0.5

y=sin(t) - 5(3+sin(t))/(10+6sin(t))^0.5

8)next integrate using symmetry about y axis that is ANS is

2*definite integral (-pi/2 to pi/2) x dy ......ydx is quite hard here but not impossible

9)use wolframalpha for easy calculation that is type this into it

2*definite integral (-pi/2 to pi/2)

( cos(t)-5cos(t)/(10+6sin(t))^0.5 )d( sin(t) - 5(3+sin(t))/(10+6sin(t))^0.5 )/dt

10)OR click this link

http://www.wolframalpha.com/input/?i=definite+integral+-pi%2F2+to+pi%2F2+%28+cos%28t%29-5cos%28t%29%2F%2810%2B6sin%28t%29%29^0.5+%29d%28+sin%28t%29+-+5%283%2Bsin%28t%29%29%2F%2810%2B6sin%28t%29%29^0.5+%29%2Fdt

Nice solution :). Did it more or less the same way...It took me about 10 minutes to type out the definite integral in wolfram alpha!...

Makes one wonder that if this is a 'simplistic' model of a leg, what the associated math of a 'realistic' model would look like. :D

Shashwat Shukla - 6 years, 3 months ago

Hi, I used a similar method . Actually I was thinking whether to solve the definite integral or use WA but I guess everyone around here knows where to go $\ddot\smile$ .

A Former Brilliant Member - 6 years, 3 months ago

Is this numerical method or not?

Lu Chee Ket - 6 years, 3 months ago

Seeu Sim's Leg

The answer is 2170.

2 solutions

0 pending reports