Semi-Circles
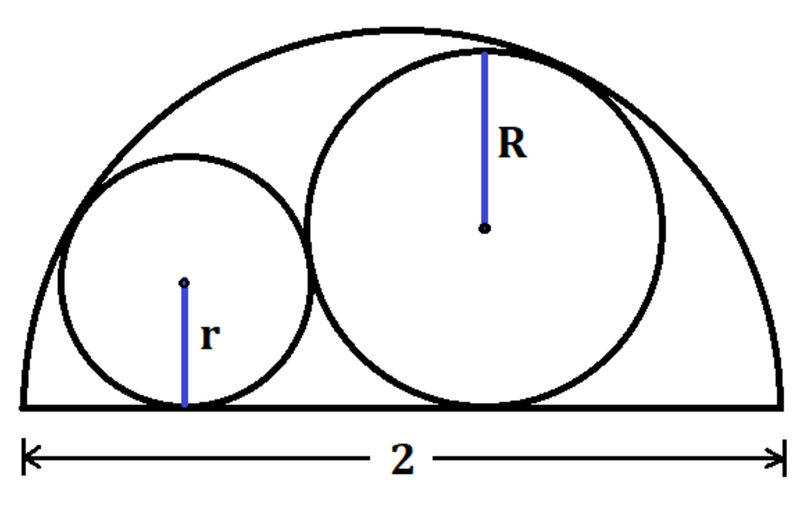
As shown in the figure, two externally tangent circles of radii R and r are internally tangent to a semicircle of diameter 2 . If R + r ≤ a ( b − c ) , find ( a + 2 b + 3 c ) ! .
The answer is 362880.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Well, if there was an equivalent to master chef for maths, i would be to classical and you would be the clever and immaginative one. I'll post a new problem soon maybe, we'll see how you solve it... -)
Log in to reply
thanks for your approbation... yeah waiting for it...
Log in to reply
Time to go to work bro https://brilliant.org/problems/revenge-of-the-progressive-sangaku/?ref_id=1592842
First, we need to express R in terms of r . We draw 3 right triangles, a pink one, a blue one and a green one
- The blue triangle gives us this equation with the pythagorean theorem : ( R + r ) ² = ( R − r ) ² + ( a + b ) ²
- The green triangle gives us this equation with the pythagorean theorem : ( 1 − R ) ² = R ² + b ²
- The pink triangle gives us this equation with the pythagorean theorem : ( 1 − r ) ² = r ² + a ²
- Next, we use the second and the third equation to express a and b in terms of r and R . Then we use substitution in the first equation to get an equation only in terms of R and r .
- The first equation becomes : 2 R r = 1 − r − R + ( 1 − 2 r ) ( 1 − 2 R
- Now we express R in terms of r and get : R = 4 r ² + 4 r + 1 − 2 r ² + 2 2 r ² − 2 r 3 + 3 r
- We can now use this fonction to express the sum R + r in terms of r :
- f ( r ) = r + 4 r ² + 4 r + 1 − 2 r ² + 2 2 r ² − 2 r 3 + 3 r
- Now set the derivative equal to 0 to find for which value of r, the function is maximum, we find r = 2 − 1
- Finally we calculate f ( 2 − 1 ) = 2 ( 2 − 1 ) so a = 2 , b = 2 , c = 1
- Then, ( 2 + 2 × 2 + 3 × 1 ) ! = 3 6 2 8 8 0
Nice approach!
Thanks. Well that's the only "rigorous" approach i could figure out...I wonder what are the others...