Serious Series

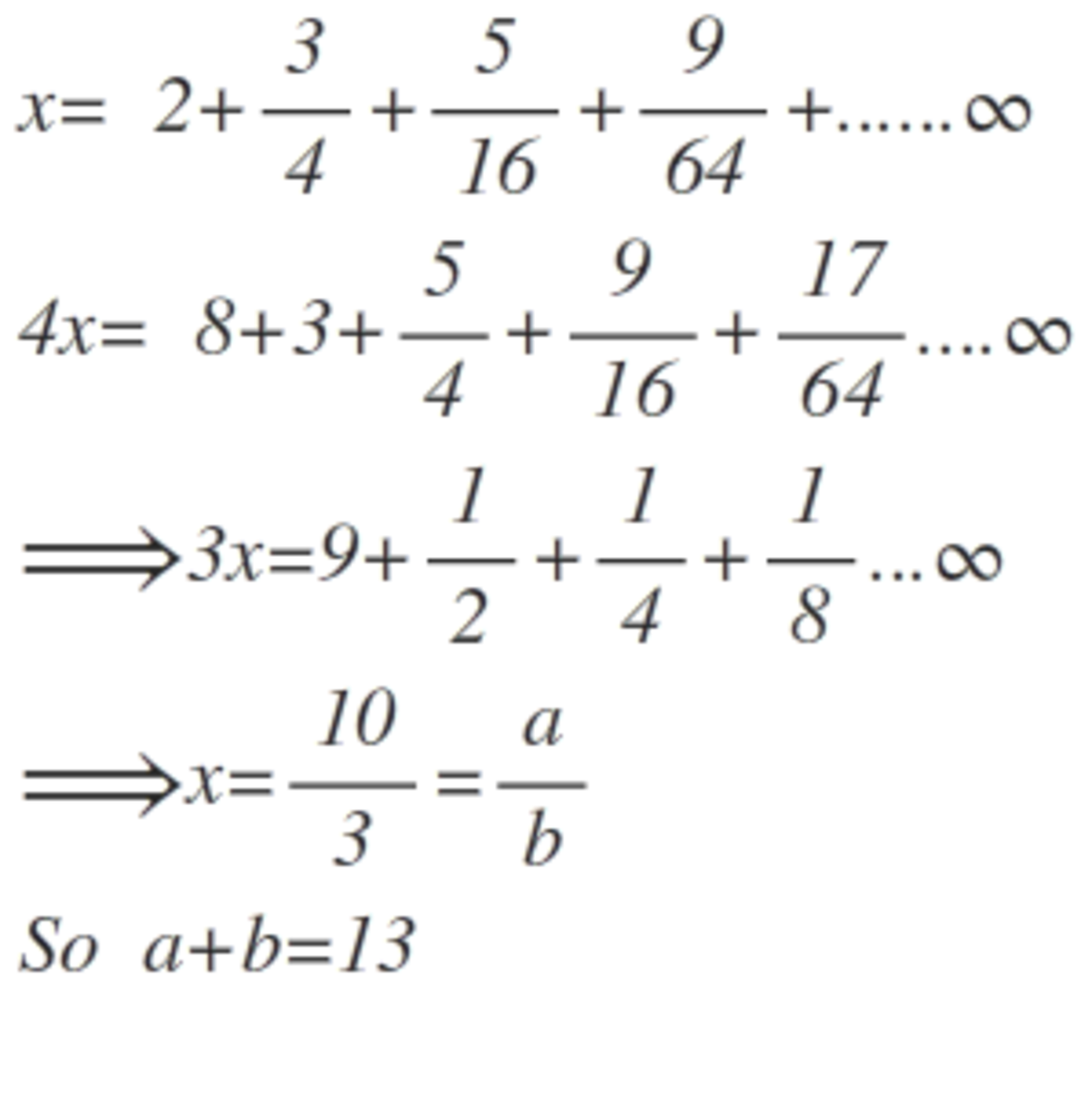
The series can be written as

$1+1,\frac{2+1}{4},\frac{2^2+1}{4^2},\frac{2^3+1}{4^3},\cdots$

which can be rewritten as

$1+1,\frac{1}{2}+\frac{1}{4},\left(\frac{1}{2}\right)^2+\left(\frac{1}{4}\right)^2,\left(\frac{1}{2}\right)^3+\left(\frac{1}{4}\right)^3,\cdots$

The series is the sum of terms of two convergent GPs both starting at 1 and with ratios $\frac{1}{2}$ and $\frac{1}{4}$ .

Thus, the required sum would be

$S = \frac{1}{1-\frac{1}{2}}+\frac{1}{1-\frac{1}{4}}=2+\frac{4}{3}=\frac{10}{3}$

Thus, $a=10,b=3,a+b=\boxed{13}$